Весь окружающий нас мир наполнен образами геометрических фигур и отношений. Поэтому изначально геометрия формировалась как наука о непосредственно наблюдаемом пространстве. И в то же время, именно геометрия больше всего вызывает трудностей у учащихся, в том числе и у студентов ссузов, чем любая другая математическая дисциплина. Эти трудности закладываются еще в школе и носят предметный и психологический характер.
В курсе изучения математики в ссузе наибольшие трудности возникают у студентов при изучении тем стереометрии и элементов аналитической геометрии (для технических специальностей). Изучение данного материала очень важно для развития пространственного представления и пространственного мышления студентов. Геометрические понятия являются идеальными объектами, среди реальных предметов подобных объектов нет. Но усвоение геометрического материала предполагает его связь с реальными объектами, выбором материальной модели геометрического объекта. Но в то же время от студентов уже требуется анализ.
Опыт преподавания стереометрии в ссузе показывает, что для многих учащихся наибольшие затруднения вызывают стереометрические задачи. При знакомстве с аксиомами стереометрии пространственные представления учащихся развиты очень слабо. Начальные сведения по стереометрии имеют абстрактный характер, усвоение материала строится на заучивании. Ученики теряют интерес к предмету, и многие из них считают стереометрию трудным школьным предметом. Трудности в изучении стереометрии вызваны тем, что зрительное восприятие геометрических объектов не всегда соответствует тем закономерностям, которыми этот объект обладает. Отображение пространственных фигур в виде чертежа на листе бумаги приводит к тому, что очень многие закономерности представляются в искаженном виде. Наглядность, которая так необходима учащимся может обеспечить изображения геометрических тел с помощью новых информационных технологий (НИТ). Существующее сегодня программное обеспечение позволяет строить перспективное изображение, поворачивать его и рассматривать под разными углами, что помогает формировать умение у учащихся воссоздавать целостный пространственный образ. Однако этому пока препятствуют отсутствие в средних специальных учебных заведениях:
· необходимой материальной базы;
· программных средств по математике;
· разработанной методики и методических указаний.
При проведении практических и лабораторных занятий по стереометрии в ссузе можно использовать следующие средства информационных технологий:
1. Flash-анимация. Они придают телам объем, позволяя наделять их свойствами пространства. В этом случае педагог должен затратить много времени для подготовки к уроку, создавая анимационные фильмы. Большое количество интерактивного материала по стереометрии можно найти на сайте Единой коллекции Цифровых образовательных ресурсов (http://school-collection.edu.ru/). Например, большой интерес представляют интерактивные задачи по стереометрии.Они содержат информационный инструмент «Конструктор фигур и сечений»- программу для создания трехмерных пространственных изображений геометрических фигур с возможностью редактирования, загрузки и сохранения содержимого области построения. То есть объекты используемы в задаче можно вращать, редактировать, сдвигать, увеличивать, делать дополнительные построения
2.Электронные стереоконструкторы. Среди распространенных платных программ можно выделить Математический конструктор, который позволяет работать в плоскости осуществлять выход в пространство. Программная среда предназначена для создания интерактивных моделей по математике, работа с которыми сочетает конструирование, эксперимент, решение задач. Учебник-справочник Стереометрия 10-11, разработанный авторским коллективом Кудиц, содержит теоретическую информацию в объеме курса средней школы, дополнительные теоремы и формулы для изучения каждой темы, задачи с указаниями к решению и ссылками, конструктор трехмерных чертежей и мультипликаций, трехмерные интерактивные иллюстрации. Данный электронный учебник построен на широком использовании возможностей современного персонального компьютера для удобного и наглядного представления учебной информации. Входящий в учебник СтереоКонструктор позволяет преподавателю совместно с учащимися создавать новые и редактировать существующие стереометрические чертежи и анимационные ролики. Создаваемые объекты (как чертёж в целом, так и отдельные его элементы) можно редактировать: изменять прозрачность плоскостей, толщину линий, положение, ориентацию, масштаб, цвет объекта. Существует возможность создавать в отдельных окнах трёхмерные и двухмерные чертежи. Инструменты Стереоконструктора, в частности, отдельные кнопки, позволяют не только выполнить построения, но и «подсказывают», какие теоретические факты лежат в основе выполнения тех или иных построений. Так, например, для построения плоскости используется специальная кнопка 
. Её изображение напоминает о том, какое количество точек и их расположение определяет единственную плоскость. Чтобы выполнить некоторые из построений, требуется знать определённые геометрические факты. Например, для построения прямой на плоскости недостаточно использовать кнопку для построения прямой: при нажатой кнопке построения прямой надо кликнуть по очереди на двух точках этой плоскости. Только после этого прямая будет построена. Чтобы построить в Стереоконструкторе перпендикулярные плоскости, нужно знать теорему: если плоскость проходит через прямую, перпендикулярную другой плоскости, то эти плоскости перпендикулярны. Тогда алгоритм выполнения построений будет выглядеть следующим образом:
• построить плоскость;
• построить прямую в этой плоскости;
• построить плоскость, перпендикулярную данной прямой.
Таким образом, использование Стереоконструктора позволяет более глубоко изучить основные аксиомы и теоремы стереометрии [2].
3. Графические символьные математические пакетов, такие как Derive, Maple, Mathematica, Maxima, MATLAB. Эти пакеты обладают большими возможностями программирования графики вплоть до создания анимированных клипов. Так весьма эффективным будет занятия с использованием математического пакета при изучении темы «Тела вращения» по учебнику для студентов техникумов и колледжей. Построение фигур, полученных от вращения вокруг оси треугольника, прямоугольника, полуокружности и т.д. позволяет закрепить понятия вращения в пространстве, будет способствовать развитию пространственного мышления учащихся.
4. Компьютерные программы, позволяющие ученикам осуществить выход в пространство. Среди программного обеспечения есть платные ресурсы, есть свободно распространяемые в сети Интернет. В начале изучения курса стереометрии перед учителем возникает проблема переноса пространственного тела в плоскость. Часто приходится строить чертежи многогранников. Если при этом возникают трудности с мысленным представлением фигуры и пониманием того, как ее можно изобразить на плоскости, из каких фигур она состоит, поможет программа Poly32. Она содержит огромную базу многогранников, каждый из которых можно визуализировать 11 способами. Можно отметить программу построения сечений SecBuilder 1.0. Выбирая один из стандартных трехмерных объектов, можно его двигать, вращать, приближать, удалять, строить сечения. Результаты можно применять в качестве иллюстраций к геометрическим задачам.
Подсистема КОМПАС-3D LT 9.0, распространяемая сегодня в школах в рамках ПНП «Образование», предназначена для создания трехмерных параметрических моделей, ориентирована на формирование трехмерных моделей конкретных тел, содержащих как типичные, так и нестандартные, уникальные конструктивные элементы. Программа позволяет строить красивые и выразительные модели пространственных конструкций. Результатом работы в данном редакторе может стать анимированный ролик или статическое изображение, просчитанное программой [1].
Рассмотрим изучение в ссузе темы «Двугранные углы». Изучение содержания программного комплекса «Стереометрия» показало возможность использования встроенного электронного учебника на любом этапе обучения: при изучении нового материала, при организации повторения, при решении задач, а также на этапе контроля знаний.
Тема «Двугранные углы» в электронном учебнике рассматривается в разделе «Многогранные углы». Все определения и теоремы сопровождаются крутящимися рисунками, что позволяет лучше рассмотреть чертёж. Теоремы представлены с доказательствами, содержащими ссылки на необходимую информацию, что даёт возможность учащимся быстро получить нужную информацию.
Объясняя новый материал, используя компьютер и видеопроектор, учитель может задействовать часть материалов ЭУ для показа готовых чертежей, представленных в ЭУ, или приготовленных им самим заранее с помощью Стереоконструктора. Учебный материал представлен наглядно. Так, например, при изучении теоремы о линейных углах двугранных углов можно в режиме реального времени посмотреть, как будет меняться линейный угол при изменении значений в статус – строке или при перемещении вершины фигуры. Таким образом, на одном рисунке можно будет увидеть все частные случаи построения линейных углов.
На этапе решения задач по данной теме можно организовать коллективную или индивидуальную работу учащихся с интерактивными задачами из Единой коллекции Цифровых образовательных ресурсов (рисунок 1). Например,
Задача. Найдите углы, образованные диагоналями куба, диагоналями его граней и основанием куба.
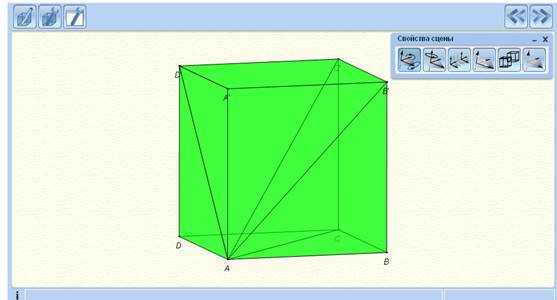
Рис. 1. Интерактивная задача по стереометрии.
Для решения данной задачи можно поэкспериментировать с моделью конструктора, задавая секущую плоскость двумя лучами и видя изображение секущей плоскости в окошке проекций. При выборе лучей, составляющих с ребром двугранного один и тот же угол β < π/2, и лежащих по одну сторону от плоскости, перпендикулярной ребру, получаются углы сечения 0 < α < φ. При выборе лучей, расположенных по разные стороны от плоскости, перпендикулярной ребру, получаются углы сечения φ < α < π.
Таким образом, учащиеся делают вывод, что углы равны 0 < α < π.
На этапе контроля знаний учащимся можно предложить тестовые задания на определение двугранного угла и его градусной меры, линейных углов для данных двугранных углов, используя при этом возможности презентации. Например, задания такого рода:
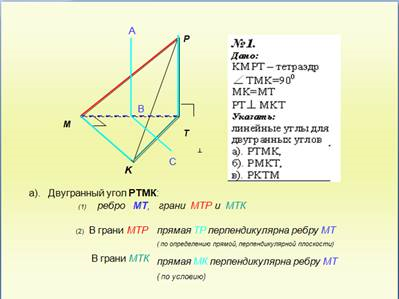
Рис. 2. Интерактивная презентация по теме «Двугранные углы»
Дистанционные технологии при изучении данной темы можно использовать для изучения дополнительного материал для тех, кому он необходим с целью ликвидации пробелов в знаниях, или, наоборот, в углублении ранее приобретенных знаний. В первом случае преподаватель подготавливает в электронной среде специальный модуль, который должен содержать определения (двугранного угла, линейного угла, величины двугранного угла), примеры на вычисление величины двугранного угла, способы построения линейного угла, способы применения теоремы о трех перпендикулярах в задачах о двугранных углах. Для развития познавательного интереса можно предложить материал по темам: «Многогранные углы», «Биссектриса двугранного угла», «Биссекторная плоскость».
Средства НИТ предоставляют широкие возможности для построения изображений геометрических фигур. Вместе с тем, использование этих средств при самостоятельном выполнении чертежей не освобождает пользователя от знакомства с теоретическими основами теории изображений. НИТ позволяют преподавателю сделать процесс обучения ярким, наглядным, динамичным, варьировать частные решения с опорой на имеющиеся готовые «шаблоны», а также более эффективно осуществлять «обратную связь». Использование компьютера позволяет повысить интерес и к математике в целом. Учащиеся активно включаются в поиск и подготовку материалов к урокам, что в свою очередь развивает у них навыки исследовательской деятельности и позволяет добиться лучших результатов.
Литература
1. Кабедева, И.Г. Об использовании электронного учебника «Стереометрия 10-11» при изучении школьного курса стереометрию.– http://www.naukapro.ru/new2007/4_002.htm.
2. Кузьмина, И.А., Применение информационных технологий при изучении школьного курса стереометрии. – http://kuzminaia.narod.ru/portfolio2.html.
