В работе исследуются колебания распределенных систем. Доказано необходимое условие замены сил инерции в однородной балке статической нагрузкой. Методом Рэлея определена собственная частота поперечных колебаний балки.
Рассмотрим детально собственные колебания однородной пролетной балки (рис. 1). Опыты показывают, что малые колебания происходят с одинаковой частотой независимо от амплитуды. Пусть имеем малые колебания, и форма балки в крайнем положении определена. Сделаем колебания вдвое меньшими. Очевидно, никакие явления не могут возникнуть или исчезнуть в малых колебаниях при уменьшении амплитуды, поскольку колебания физически неразличимы. Тогда и отклонение каждой точки балки уменьшится ровно вдвое.
Остановим балку в крайнем положении, тогда ее форма будет формой колебаний. Силы инерции, распределенные по длине балки, будут пропорциональны ее отклонению от положения равновесия.
Если приложить нагрузку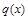 
, пропорциональную прогибу то, очевидно, форма балки сохранится. Заметим одно важное обстоятельство: инерционные силы каждого элементарного участка длины балки пропорциональны отклонению этого участка от положения равновесия. Следовательно, эпюр распределенной нагрузки полностью повторяет форму изогнутой оси балки.
Используем известный из сопротивления материалов факт, что уравнение изогнутой оси тонкой балки получается путем двойного интегрирования распределенной нагрузки. Следовательно, уравнение нагрузки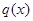 
должно быть таким, чтобы не измениться после интегрирования. Этому условию соответствует экспонента или синусоида. По условиям закрепления остановимся на синусоиде (рис. 1) и запишем нагрузку в виде
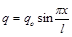, (1)
где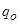 
- наибольшее значение нагрузки, Н/м.
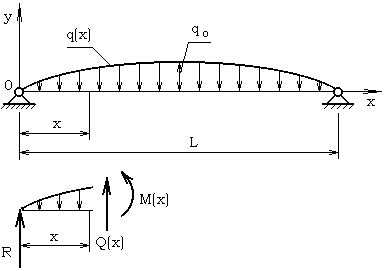
Рисунок 1 – Эпюр поперечной динамической нагрузки
Из условия равновесия сумма проекций всех сил на вертикальную ось равна нулю
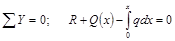, (2)
где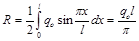 
реакция опоры.
Поперечная сила в сечении балки
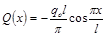(3)
Сумма моментов вокруг оси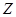 
(нормально к плоскости рисунка)
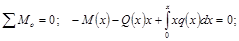(4)
После интегрирования получим
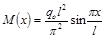(5)
Уравнение угла поворота сечения тонкой балки имеет вид
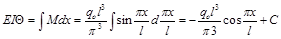(6)
В середине пролета балки угол поворота сечения равен нулю, т.е. для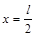 
можно записать 
,
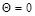тогда произвольная постоянная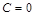 
.
Окончательно угол поворота любого сечения балки равен
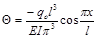(7)
Проинтегрируем уравнение угла поворота и получим уравнение прогиба балки
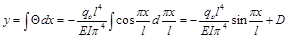(8)
На опорах прогиб балки равен нулю, что равносильно условию:
для 
, тогда произвольная постоянная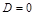 
.
Окончательно прогиб любого сечения балки равен
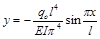(9)
Итак, форма изогнутой балки в точности соответствует эпюру выбранной нами ранее распределенной нагрузки. Поправочный множитель перед синусом характеризует жесткость балки, а по размерности служит для перевода распределенной нагрузки в прогиб. Этим доказано необходимое условие замены сил инерции статической нагрузкой. Возможно, этого доказательства не достаточно, но можно надеяться, что никакая другая, естественная с точки зрения инженера функция не подойдет в качестве нагрузки.
В соответствии с методом Рэлея квадрат собственной частоты равен отношению средней жесткости к средней массе.
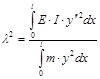, (10)
где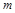 
- удельная масса балки, кг/м.
Подстановка второй производной по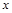 
от (9) в числитель и (9) в знаменатель дает квадрат частоты
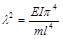(11)
Эту частоту принято называть первой или первым тоном. Первый тон самый низкий и наиболее точно воспроизводимый в эксперименте. Отметим резкую зависимость частоты от длины балки, что позволяет эффективно уходить от резонансов, например, при проектировании судов.
Имеются и другие формы колебаний. Рассмотрим две одинаковые балки (рис. 2) вибрирующие в противофазе с одинаковой амплитудой.
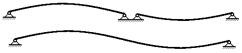
Рисунок 2 – Безузловая и одноузловая форма колебаний
Реакции в смежных опорах равны и противоположны, углы поворота смежных сечений совпадают, что позволяет мысленно объединить балки и убрать опоры в средней части. Новая сдвоенная балка колеблется с двумя максимумами и одним узлом на той же частоте что и две короткие балки. Форма колебаний называется одноузловой. Если этой балке задать старую форму колебаний, то частота уменьшится вчетверо. В общем случае колебаний тонкой балки её форма содержит множество простых форм с дискретными частотами. На рис. 3 показана форма колебаний, составленная из трех простых форм
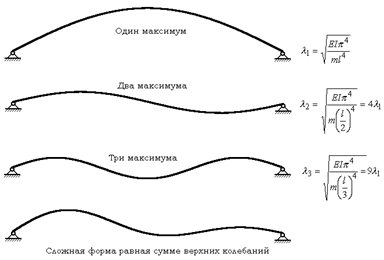
Рисунок 3 – Сложение форм колебаний балки
Теоретическое количество форм колебаний бесконечно велико, но в реальных системах ограничено тем, что другие явления начинают доминировать, и маскируют рассмотренные колебания. Прежде всего, следует указать на сдвиговые колебания балки, на податливость опор и на распространение упругих волн вдоль сечения.
Продольные колебания судовых перекрытий можно представить как продольные колебания однородного стержня закрепленного по концам (рис. 4).
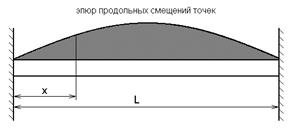
Рисунок 4 – Эпюр продольных смещений
Формула для собственной частоты стержня выводится значительно проще, поэтому опускаем вывод.
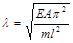, (12)
где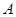 
- площадь поперечного сечения стержня.
Интересно то, что в стержне частота обратно зависит от длины, а численное значение частоты для типичных судовых конструкций намного выше, чем для поперечных колебаний. Например, для перекрытия между шпациями имеем следующие параметры конструкции:
· толщина листа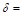 
8 мм;
· длина пролета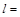 
500 мм;
· модуль упругости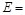 
200 ГПа;
· плотность материала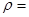 
7800 кг/м3.
Выделим часть обшивки шириной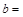 
1 м, тогда удельная масса
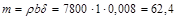кг/м
Момент инерции сечения
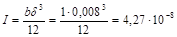м4
Площадь сечения
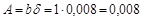м2
Частота поперечных колебаний обшивки
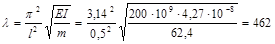с-1
Частота продольных колебаний
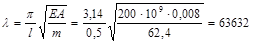с-1
Подойдем к этому вопросу с другой стороны. Представим колебания стержня между стенками как бегущую волну. Тогда волна деформации проходит от одного конца до другого и обратно за один период. Частота колебаний, обратная периоду, равна скорости звука деленной на удвоенную длину стержня.
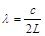(13)
Для скорости звука в упругой среде Ньютоном была предложена формула
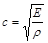, (14)
где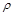 
- плотность среды.
Плотность можно записать как массу стержня, деленную на его объем, а массу как удельную массу, умноженную на длину. Тогда наша формула принимает вид
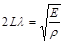. (15)
Это совпадает с формулой Ньютона, которая доставила ему много хлопот. Дело в том, что для газов эта формула дает небольшую, но систематическую ошибку. Когда Ньютон измерял упругость газов, не было понятия изохорная и изобарная теплоемкость. Газовые законы откроют через сто лет. Для медленно сжатого газа теплоемкость больше, а упругость меньше. Это и давало немного меньшую скорость звука в воздухе. Любой инженер может измерить скорость звука и достаточно точно. Для этого нужно встать напротив отвесной стены и стучать молотком. Подбирая частоту так, чтобы собственные и отраженные удары интерферировали можно посчитать число ударов в минуту. Измерив, расстояние до стены, можно вычислить скорость звука.
В стержне (рельс или кусок длинной проволоки) получается скорость звука близко к 5100 м/с. Посмотрим, что дает формула Ньютона.
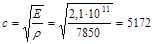м/с (16)
Как видно совпадение очень хорошее – 1,4%. Подводя итог, заметим, что наш метод и метод Ньютона дают одинаковый результат.
