In this paper, the goal is the determination of electric field distribution and concentration in an isotropic conductive medium inside a channel of constant cross section, the upper and lower walls of which are partly the electrodes, and partly insulators.
Keywords: the electric field, concentration, electrodes, transistor.
В данном случае электрическое поле потенциально, т. е. его можно представить, как градиент некоторого потенциала.
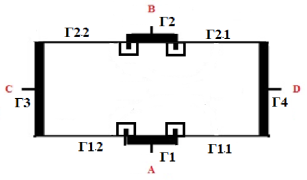
Рис. 1. Расчетная схема транзистора Шоттки
Для введенного потенциала можно сформулировать краевую задачу.
В плоской области A и B (верхняя и нижняя границы) найти решение уравнения Лапласа
(1)
со смешанными граничными условиями.
На электродах задаются потенциалы (Vз-на затворе, Vи-на эмиттере):
.
(2)
На изоляционных стенках нормальная составляющая плотности тока 
. Откуда следует граничное условие для потенциала на верхнем и нижнем изоляторах:
(3)
Для решения задачи (1.1) — (1.3) в окрестностях стыков электродов и изоляторов использовалось разложение потенциала в ряд Фурье, которое получается из аналитического решения задачи о распределении потенциала электрического поля вблизи края заряженной полуплоскости.
Решая методом разделения переменных, получаем представление искомой функции в полярных координатах
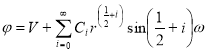,(4)
где коэффициенты ряда определяются по общему правилу как коэффициенты ряда Фурье.
Расчетная область разбивается прямоугольной сеткой с постоянным шагом
(hx=lx/(nx-1), hy=ly/(ny-1). Точки стыка размещаются в узлах сетки. Расчет производился на сетках 80х26, что позволило определить влияние сгущения узлов сетки для более точного определения потенциала вблизи точек особенности. Задача с граничными условиями решалась численно.
Дифференциальное уравнение аппроксимируется общепринятой центральной разностной схемой типа «крест», и решение в них определяется итерационным методом Гаусса-Зейделя. Верхняя (А) и нижняя (В) граница разбиваются на три одинаковых отрезка. На середине отрезка верхней и нижней границе задаются параметры решения уравнения Лапласа.
При расчете концентрации использовался метод Лакса, который имеет второй порядок и имеет характер сглаживания, поэтому в данном случае наиболее подходящий.
В процессе решения задачи также использовались ниже приведенные формулы:
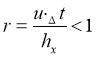(5)
где u — компонента скорости перемещения электронов, t — время, hx — шаг.
Компоненты скорости определялись как произведения компонентов производных токов (1.7) и удельной проводимости проводника:
(6)
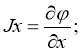
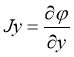(7)
Расчетное время также определялось двумя компонентами:
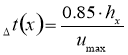
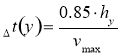(8)
Расчет проходили в несколько этапов:
1) Определение методом Гаусса -Зейделя значений функции в узлах области А и В;
2) Определение производных диффузионных токов Jx, Jy.
3) Вычисление времени, скоростей и концентрации распространения заряженных частиц в расчетной области.
4) Вычисление коэффициентов разложения C1,C2 для областей на границах Г1-Г1.2, затем для границ Г2.1-Г2, Г2-Г2.2 и Г1-Г1.2;
5) Вычисления значений потенциала в узлах особых областях
Заключение
В работе проводились исследования на величину потенциала затвора, позволяющие определить его влияние на характер прохождения электронов. В результате, чем выше значение потенциала на затворе, тем выше вероятность запирания транзистора.
Показано, что для исследуемой модели транзистора определение с высокой точностью полей электрической напряженности в местах стыка электрода и изолятора большого значения не имеет, в связи с тем, что окончательное запирание канала происходит на центральной оси устройства и максимально удалено от мест особенности.
Литература:
- Васенин И. М., Нариманов Р. К. Определение параметров магнитогидродинамического течения в канале МГД-генератора с учетом краевых эффектов электрического поля., г. Томск, 2006.
- Вячистый Д. Ф., Нариманов Р. К. Гидродинамическая двумерная модель GaAs полевого транзистора Шоттки с учетом особенностей электрического поля., г. Томск, 2006.
- Иващенко В. М., Митин В. В. Моделирование кинетических явлений в полупроводниках. Метод Монте-Карло. — К.: Наукова думка, 1990.- 192 с.
- Флетчер К.. Вычислительные методы в динамики жидкостей 1–2 Тома- Мир, Москва, 1991.
- Kohn E. V-shaped-gate GaAs MESFET for improved high frequency performance//Electronics Letters, 1975, V.11, № 8, p.160.
- Wang Y. J., Lu S. S. Two-dimensional simulation for the GaAs V-groove gate MESFET's // Solid State Electronics, 1999, V.43, № 2, p.229.
