В статье рассмотрены и установлены параметры тормозов подлежащих моделированию, эффективность системы контроля элементов и узлов тормозной системы. Разработана математическая модель определения упреждающего допуска элементов тормозов.
Ключевые слова: тормозная система, моделирование, дифференциальные уравнение, подъемно-транспортная и строительно-дорожная машина.
При исследовании тормозных систем подъемно-транспортных и строительно-дорожных машин ПТСДМ некоторые неявные вопросы становятся реальными использовании процесса моделирования. В этом случае следует определить основные параметры тормозной системы, подлежащие процессу моделирования. Следует отметить, что в моделях эксплуатации ПТСДМ с тормозными системами параметрами подлежащих моделированию могут быть: режим работы тормозов; продолжительность их цикла или процесса выполнения технической операции; характер воздействия эксплуатационных нагрузок и окружающей среды на тормоза; время восстановления элементов и узлов тормозов; изменения технического состояния элементов тормозных систем и т. д. Кроме вышеуказанных факторов следует установить влияние на эксплуатационные параметры тормозных систем достоверности результатов контроля и качества восстановления элементов тормозов. Данный подход имеет две цели: установление количественных соотношений, описывающих влияние данных компонентов на параметры системы эксплуатации тормозов ПТСДМ, и оценить устойчивость системы эксплуатации тормозов к погрешностям исходных данных. Как известно, устойчивость любой системы, в том числе тормозной, характеризуется как свойство, связанное с затуханием реакции, данной системы на возбуждающее воздействие.
При возможности описания поведения системы эксплуатации тормозов ПТСДМ с использованием дифференциальных уравнений, то исследование устойчивости представляло бы собой анализ решений данных уравнений. Хотя данный процесс является достаточно сложным и трудоемким, в принципе выполняемый на основе теории Ляпунова об устойчивости движения.
Хотя большинство факторов, необходимые для учета при описании системы эксплуатации тормозов, являются недифференцируемыми функциями, случайности в законе изменения параметров такой системы не позволяют описать её с помощью дифференциальных уравнений. Следовательно, устойчивость исследуется на базе статистического моделирования процесса эксплуатации тормозной системы. В этом случае возмущающие воздействия рассматриваются как погрешности в исходных данных и случайности в принимаемых решениях на восстановление элементов и узлов тормозной системы. Реакция элементов и узлов тормозной системы описывается выше рассмотренными показателями. Поэтому необходимо определить значение этих показателей в функции от возмущающих воздействий на тормозную систему ПТСДМ и установить характер их изменения во время моделирования. Необходимо рассмотреть вопросы, связанные с моделированием достоверности контроля и качества восстановления элементов и узлов и оценкой их влияния на введенные выше показатели. Следует отметить, что эффективность системы контроля элементов и узлов тормозной системы с точки зрения корректного заключения о состоянии контролируемого объекта, оценивается достоверностью результатов контроля H, которая связана с вероятностями ошибок первого и второго рода соотношением
![]()
где α — вероятность появления ошибок 1-го рода (неисправным признан фактически исправный объект); β — вероятность появления ошибок 2-го рода (исправный объект признан неисправным). Дополнительные проверки и ремонтно-регулировочные работы вызваны ошибками первого рода, что увеличивает трудозатраты на обслуживание. На эксплуатационные показатели тормозов ошибки второго рода непосредственно не влияют, поэтому примем β=0.
Знание плотности вероятности случайных погрешностей p(X/α)измерительного тракта системы контроля позволяет производить расчет погрешностей измерения. Данный тракт включает в себя совокупность устройств (датчики, линии связи, коммутатор, преобразователи, нормализаторы и т. д.), каждое из которых вносит погрешность в результат измерения. Следует учесть, что при проектировании систем контроля предполагается о приблизительном равенстве и независимости погрешности. Данный момент позволяет считать распределение суммарной погрешности нормальным:
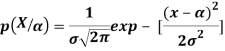
где p(X/α) — плотность вероятности измеренных значений при условии, что истинное значение измеряемой величины равно α; x — результат наблюдения; ![]() — средняя квадратичная погрешность результата наблюдения.
— средняя квадратичная погрешность результата наблюдения.
Эксплуатация подъемно-транспортных и строительно-дорожных машин и оборудования с тормозными системами позволяет, а так же с введением упреждающего допуска позволяет получить ряд преимуществ по сравнению с эксплуатацией тормозной системы до отказа. Следует отметить, что, в свою очередь, предъявляет повышенные требования к точности его определения.
Следует удостовериться в том, что метод определения упреждающего допуска, базирующийся на решении задачи линейного программирования, позволяет точно вычислить его значение. При этом возникает задача оценки достоверности решения задачи линейного программирования. Правильность решения задачи линейного программирования заключается в получении решения данной задачи другим методом, принципиально отличающимся от первого. Применительно к задаче линейного программирования выбрать — в качестве контрольного метода — метод статистического моделирования. Выбор данного метода обусловлен простотой его реализации, наглядностью и легкостью интерпретации промежуточных и конечных результатов, а так же возможностью их получения с любой наперед заданной точностью, хотя последнее свойство метода связанно с увеличением объема расчетов.
Принцип определения упреждающего допуска заключается в следующем: формулируется основная цель; рассматривается процесс эксплуатации тормозных систем ПТСДМ и взаимодействие блоков алгоритма и т. д.
Основная цель заключается в том, что для заданного случайного процесса следует установить такое значение t*, которое позволяет достичь минимума средних удельных затрат при значительной по срокам эксплуатации тормозных систем ПТСДМ (строго, при t →∞).
Процесс эксплуатации тормозной системы восстановление элементов которой производится только при отказе (t*=F). Если T — суммарное время наработки, в течение которого было совершенно n (T) восстановлений элементов тормозной системы ПТСДМ, при этом каждое восстановление элемента тормоза требует Tp чел.ч. В этом случае оценка средних удельных затрат ![]() . Примем далее некоторый допуск di˂ F при достижении которого следует производить предупредительные работы со средними затратами Tn ˂ Tp. Считаем, что за время наработки T должно быть выполнено определенное число восстановлений элементов тормоза после его отказа n1(T) ˂ n(T) и некоторое количество восстановлений элементов тормозной системы типа предупредительных работ n2(T). Для данного случая оценку средних удельных затрат необходимо вычислить по зависимости:
. Примем далее некоторый допуск di˂ F при достижении которого следует производить предупредительные работы со средними затратами Tn ˂ Tp. Считаем, что за время наработки T должно быть выполнено определенное число восстановлений элементов тормоза после его отказа n1(T) ˂ n(T) и некоторое количество восстановлений элементов тормозной системы типа предупредительных работ n2(T). Для данного случая оценку средних удельных затрат необходимо вычислить по зависимости:
![]()
Очевидно, что при варьировании значения величины I также будут измеряться величины ![]() и
и![]() , а так же и значение величины
, а так же и значение величины ![]() . При изменении значения i и фиксирование количества
. При изменении значения i и фиксирование количества ![]() и
и![]() , на основе зависимости (3) можно получить зависимость
, на основе зависимости (3) можно получить зависимость ![]() . Кривая данного выражения имеет в наличии единственный минимум по i, который размещается как внутри, так и на границе области работоспособности тормозной системы. Произведя выборку из полученной совокупности величин
. Кривая данного выражения имеет в наличии единственный минимум по i, который размещается как внутри, так и на границе области работоспособности тормозной системы. Произведя выборку из полученной совокупности величин ![]() и найдя минимальное значение, определим соответствующее ему упреждающим допуск i, который и будет оптимальным по выбранному критерию.
и найдя минимальное значение, определим соответствующее ему упреждающим допуск i, который и будет оптимальным по выбранному критерию.
Следует указать, что оценка величины ![]() . производилась для простоты и удобства расчетов не для абсолютных значений Tnи Tp, а для нормированной величины
. производилась для простоты и удобства расчетов не для абсолютных значений Tnи Tp, а для нормированной величины ![]() , 0 ≤
, 0 ≤![]() ≤ 1. Для вычисления искомого значения средних удельных затрат
≤ 1. Для вычисления искомого значения средних удельных затрат 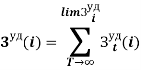 . необходимо значительное по сроку время моделирования. Для практических расчетов величину T необходимо выбирать из условия, чтобы две соседние оценки
. необходимо значительное по сроку время моделирования. Для практических расчетов величину T необходимо выбирать из условия, чтобы две соседние оценки ![]() и
и ![]() не отличались более, чем на заранее заданную малую величину
не отличались более, чем на заранее заданную малую величину ![]() , т. е.
, т. е. ![]() , где k=1,2,3,... Однако при таком подходе есть одна особенность: оценка
, где k=1,2,3,... Однако при таком подходе есть одна особенность: оценка ![]() является случайной величиной, а для того чтобы данная величина являлась статистически устойчивой, необходимо ее усреднить по множеству. Для этой цели при конкретном k=1,2,3,... вычисляют такие средние значения, чтобы модуль их разности не превышали
является случайной величиной, а для того чтобы данная величина являлась статистически устойчивой, необходимо ее усреднить по множеству. Для этой цели при конкретном k=1,2,3,... вычисляют такие средние значения, чтобы модуль их разности не превышали ![]() . С целью выполнения данного условия величина
. С целью выполнения данного условия величина 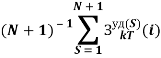 выбирается в качестве оценки для
выбирается в качестве оценки для ![]() , в дальнейшем используемая для принятия решения об окончании моделирования и вычисления величины
, в дальнейшем используемая для принятия решения об окончании моделирования и вычисления величины ![]() .
.
На рисунке 1 показано взаимодействие блоков алгоритма, обеспечивающее решение данной задачи. Следует отметить, что оператором 1 вводятся следующие исходные параметры: матрица значений вероятностей переходов Bn, значение точности вычислений ![]() , нормированные затраты
, нормированные затраты ![]() . Цепь Маркова [1,2]моделирует оператор 2. Сравнение текущего состояния цепи Маркова с выбранным значением упреждающего допуска dупр или с границей отказа F осуществляется в операторе 3.
. Цепь Маркова [1,2]моделирует оператор 2. Сравнение текущего состояния цепи Маркова с выбранным значением упреждающего допуска dупр или с границей отказа F осуществляется в операторе 3.
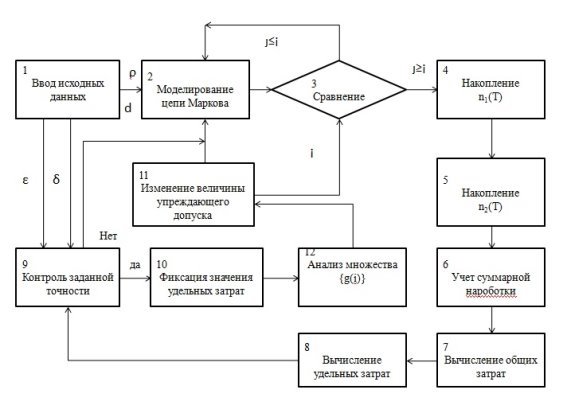
Рис. 1. Алгоритм определения момента оптимальной остановки
В зависимости от полученного результата сравнения фиксируется либо ремонт, либо упредительное восстановление элементов тормозной системы ПТСДМ и производится раздельное накопление их числа с помощью операторов 4 и 5. Оператор 6 суммирует числа шагов моделирования, что эквивалентно накоплению значения наработки. Следует указать, что достижение текущей наработки значения T обеспечивается вычислением общих затрат за этот период (см. оператор 7) и удельных затрат (см. оператор 8). В дальнейшем производится контроль точности (см. оператор 9) в начале по величине ![]() , а далее по величине
, а далее по величине ![]() . При недостижении точности процесс моделирования повторяется, в этом случае изменяется сначала количество реализации при каждом T, а затем величина K.
. При недостижении точности процесс моделирования повторяется, в этом случае изменяется сначала количество реализации при каждом T, а затем величина K.
При выдерживании требований по точности операто 10 фиксирует вычисленное значение ![]() , оператор 11 изменяет значение i, и процесс повторяется до тех пор, пока не будут исчерпаны все заданные значения i. В полученной выборке
, оператор 11 изменяет значение i, и процесс повторяется до тех пор, пока не будут исчерпаны все заданные значения i. В полученной выборке ![]() устанавливается значение:
устанавливается значение:
![]()
которая определяет упреждающий допуск i*. Для уменьшения объема вычислений вариация i должно производиться так, чтобы начальное значение было ровно F, что позволяет при проведении анализа полученных значений ![]() (см. оператор 12), останавливать моделирование тогда, когда первый раз будет получено минимальное значение
(см. оператор 12), останавливать моделирование тогда, когда первый раз будет получено минимальное значение ![]() , определяемая по факту, при очередном значении
, определяемая по факту, при очередном значении ![]() .
.
Анализ выражения (4) позволяет определить минимальное значение средних удельных затрат и соответствующие им оптимальные упреждающие допуски. Сравнение значений ![]() полученные на основе метода статистического моделирования и решения задачи линейного программирования, позволяет доказать их идентичность, что обеспечивает их достоверность результатов, полученных в результате применения алгоритма:
полученные на основе метода статистического моделирования и решения задачи линейного программирования, позволяет доказать их идентичность, что обеспечивает их достоверность результатов, полученных в результате применения алгоритма:
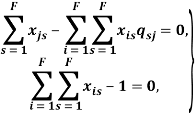
Заключение
На основе анализа установлены параметры тормозов подлежащих моделированию: режим работы; продолжительность их цикла или процесса выполнения технологических операций; характер воздействия эксплуатационных нагрузок и окружающей среды на тормоза; время восстановления элементов и узлов тормозов; изменения технического состояния элементов тормозных систем и т. д.
Установлена эффективность системы контроля элементов и узлов тормозной системы. Разработан принцип определения упреждающего допуска элементов тормозов. На рисунке приведено взаимодействие блоков алгоритма, обеспечивающие решение задачи моделирования тормозной системы. Анализ полученных выражений позволяет определить минимальное значение средних удельных затрат и соответствующие им оптимальные упреждающие допуски.
Литература:
Тихонов В. И. Выбросы случайных процессов. М.: Наука, 1987.632 с.
Бусленко Н. П. Моделирование сложных систем. М.: Наука 1988. 388с.







