Моделирование системы АИН ШИМ — асинхронный двигатель с переменными 
в неподвижной системе координат αβ
Емельянов Александр Александрович, доцент;
Бесклеткин Виктор Викторович, ассистент;
Авдеев Александр Сергеевич, студент;
Чернов Михаил Владимирович, студент;
Киряков Георгий Анатольевич, студент;
Габзалилов Эльвир Фиргатович, студент
Российский государственный профессионально-педагогический университет (г. Екатеринбург)
В данной работе рассматривается процесс математического моделирования асинхронного двигателя [1] при питании от трехфазного автономного инвертора напряжения с широтно-импульсной модуляцией (АИН ШИМ). Результаты этой работы будут основой для создания учебно-лабораторной установки по исследованию системы АИН ШИМ – АД. Функциональная схема системы трехфазный автономный инвертор с ШИМ – асинхронный двигатель приведен на рис. 1.
Рис. 1. Функциональная схема системы «АИН ШИМ – АД»
В этой схеме приняты следующие обозначения:
– задающие гармонические воздействия:
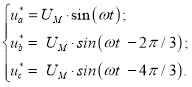(1)
uоп – опорное напряжение, представляющее собой пилообразное, двухстороннее, симметричное напряжение с частотой модуляции значительно превышающей частоту напряжения задания. Математическая модель генератора пилообразного напряжения и его выходные сигналы даны на рис. 2, 3 и 4;
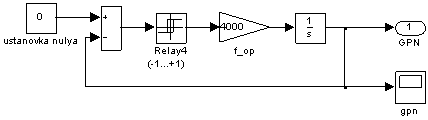
Рис. 2. Генератор пилообразного напряжения
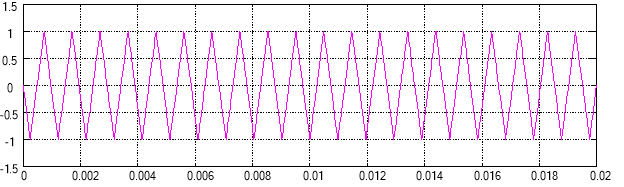
Рис. 3. Выходной сигнал генератора пилообразного напряжения
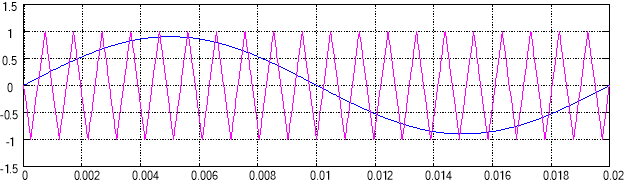
Рис. 4. Сравнение выходного сигнала генератора с задающим гармоническим воздействием 
НОа, НОb и НОс – нуль-органы, обеспечивающие сравнение сигналов задания с опорным сигналом. Если
, то выходные сигналы нуль-органов 
, иначе
;
Ф1а и Ф2а, Ф1b и Ф2b, Ф1с и Ф2с – формирователи сигналов управления силовыми ключами. Формирователи сигналов управления имеют взаимно инверсные релейные характеристики [2] и сепарируют сигнал нуль-органа НО по двум каналам управления ключами инвертора. Кроме того, предусматривают небольшие временные задержки включения ключей. Это необходимо для предотвращения коротких замыканий источника постоянного напряжения uп через силовые ключи инвертора;
и
и
и
– дискретные выходные сигналы с формирователей, управляющих включением силовыми ключами;
1А и 2А, 1В и 2В, 1С и 2С – силовые ключи, попеременно подключающие обмотки фаз двигателя к разноименным полюсам источника постоянного напряжения uп.
В каждом из состояний инвертора две фазы двигателя с помощью ключей соединены параллельно и подключены к источнику питания последовательно с третьей фазой. Поэтому напряжение источника питания распределяется между фазами нагрузки (в случае их симметрии) следующим образом: одна треть величины напряжения приходится на каждую из параллельно включенных фаз и две трети – на последовательно включенную фазу (таблица 1) [2].
Таблица 1
|
Номер комбинации |
Состояния схемы |
|||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
|
Включение ключей |
1А 2В 2С |
1А 1В 2С |
2А 1В 2С |
2А 1В 1С |
2А 2В 1С |
1А 2В 1С |
1А 1В 1С |
2А 2В 2С |
|
Схема питания обмоток АД |
|
|
|
|
|
|
|
|
Формирователи сигналов управления силовыми ключами (Ф1а и Ф2а, Ф1b и Ф2b, Ф1с и Ф2с) задают программу подключения фаз обмоток двигателя к источнику постоянного напряжения uп.
Фазное напряжение в обмотке двигателя представляет собой пятиуровневую импульсную функцию [2] со значениями:
Импульсные напряжения, подаваемые на двигатель 
связаны с постоянным напряжением uп и выходными сигналами нуль-органов 
и 
(рис. 5) по следующей зависимости 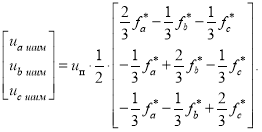[2]:
(2)
Рис. 5. Сигналы 
, 
и 
на выходе нуль-органов
Реализация импульсных напряжений 
в неподвижной трехфазной системе координат abcпредставлена в Simulink-Matlab на рис. 6. Результаты моделирования напряжений даны на рис. 7.
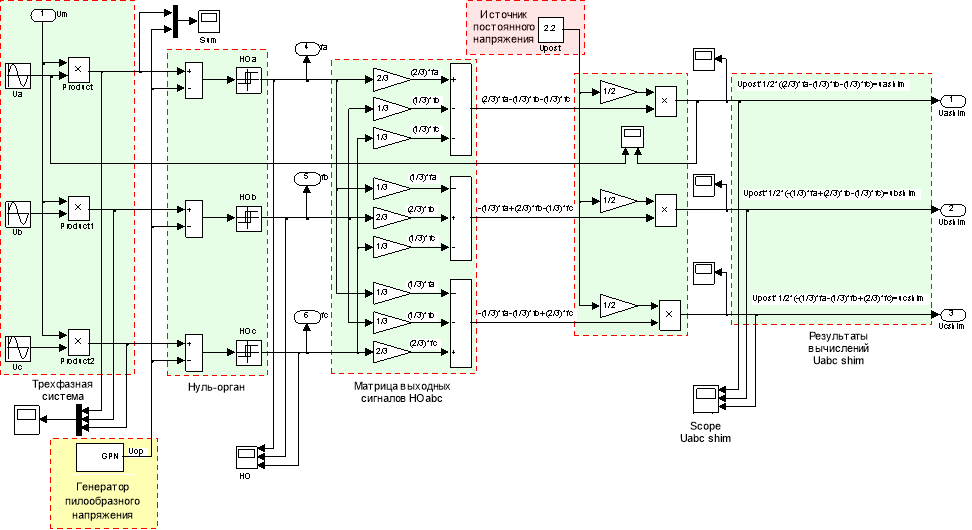
Рис. 6. Математическая модель реализации зависимости (2) в Matlab
Рис. 7. Выходные напряжения в неподвижной трехфазной системе координат
Далее эти напряжения из трехфазной системы преобразуются в импульсные двухфазные напряжения в неподвижной декартовой системе координат αβ по следующим формулам [2]:
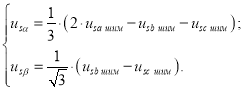(3)
Математическая модель этих уравнений в Simulink-Matlab дана на рис. 8.
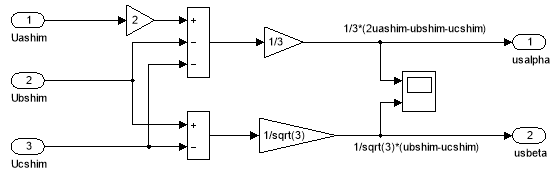
Рис. 8. Прямое преобразование координат «abc → αβ»
Выходные сигналы этого преобразователя даны на рис. 9.
Рис. 9. Напряжения 
на выходе прямого преобразования координат
Напряжения воздействуют на математическую модель асинхронного двигателя, рассмотренную в статье [1]. Статорные токи 
в неподвижной двухфазной системе координат αβ (рис. 10) с помощью обратного преобразователя координат трансформируется в неподвижную трехфазную систему координат 
.
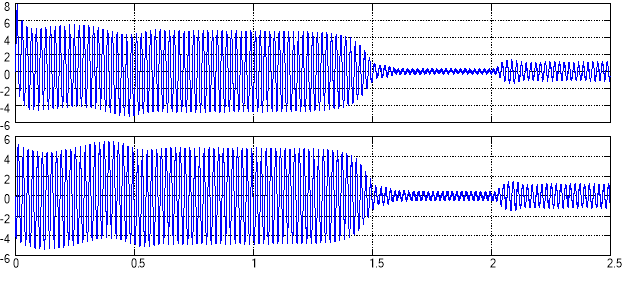
Рис. 10. Статорные токи в неподвижной системе координат на входе обратного преобразователя координат
Обратные преобразования производятся по следующим формулам [2]:
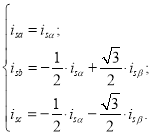(4)
Математическая модель обратного преобразования и результаты 
и 
даны на рис. 11, 12 и 13.
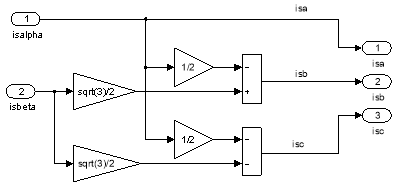
Рис. 11. Математическая модель обратного преобразования токов в неподвижной системе координат «αβ → abc»
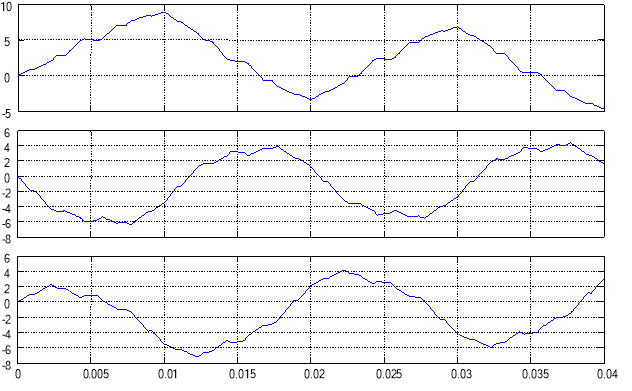
Рис. 12. Статорные токи и на выходе обратного преобразователя координат при частоте генератора пилообразного напряжения fоп = 1000 Гц
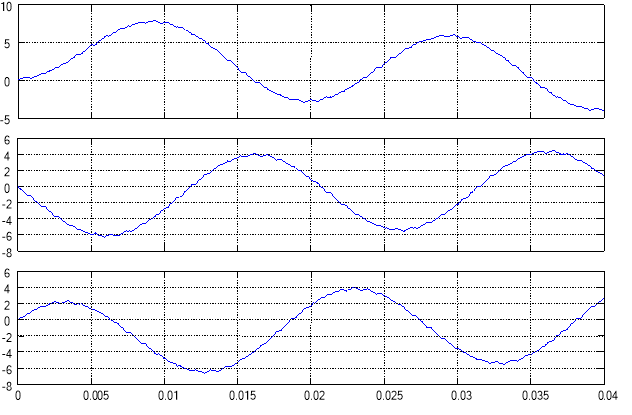
Рис. 13. Статорные токи и на выходе обратного преобразователя координат при частоте генератора пилообразного напряжения fоп = 4000 Гц
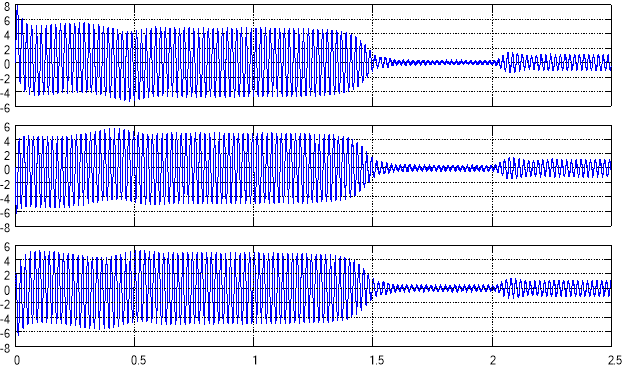
Рис. 14. Статорные токи и на выходе обратного преобразователя координат
при частоте генератора пилообразного напряжения fоп = 4000 Гц и времени t = 2,5 c
Полная схема математической модели АИН ШИМ – АД дана на рис. 15.
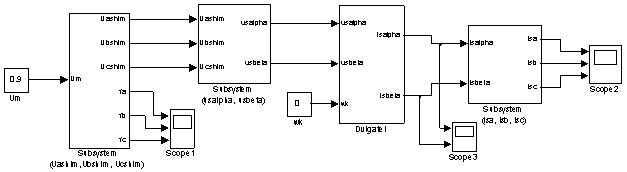
Рис. 15. Полная схема системы АИН ШИМ - АД
Электромагнитный момент и скорость асинхронного двигателя при питании от АИН ШИМ представлены на рис. 16.
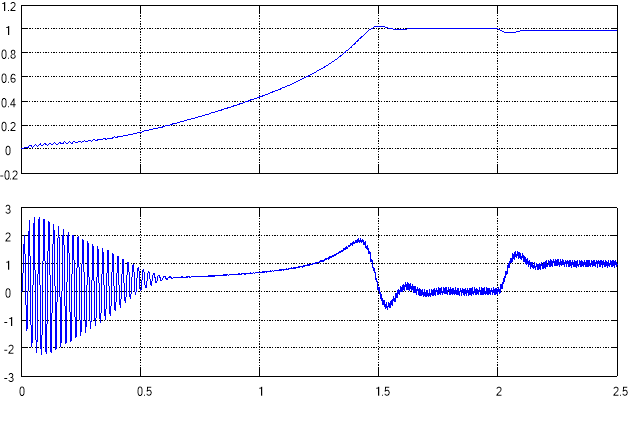
Рис. 16. Момент и скорость двигателя при питании от АИН ШИМ
Математическая модель асинхронного двигателя [1] дана на рис. 17.
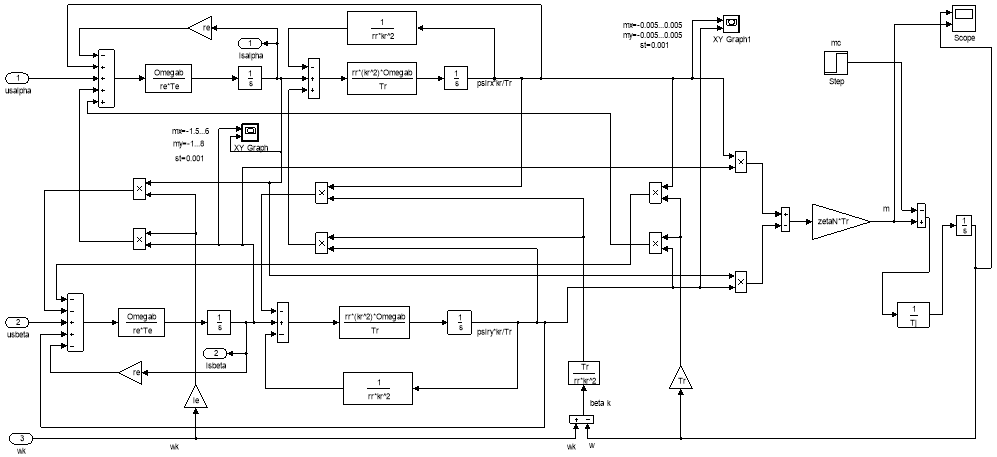
Рис. 17. Математическая модель асинхронного двигателя на основе интегрирующих звеньев
Расчет параметров асинхронного двигателя [1], [3]:
%Номинальные данные
PN=320000;
UsN=380;
IsN=324;
fN=50;
Omega0N=104.7;
OmegaN=102.83;
nN=0.944;
cos_phiN=0.92;
zp=3;
%Параметры Т-образной схемы замещения при номинальной частоте
Rs=0.0178;
Xs=0.118;
Rr=0.0194;
Xr=0.123;
Xm=4.552;
J=28;
%Базисные величины системы относительных единиц
Ub=sqrt(2)*UsN;
Ib=sqrt(2)*IsN;
OmegasN=2*pi*fN;
Omegab=OmegasN;
Omegarb=Omegab/zp;
Zb=Ub/Ib;
Psib=Ub/Omegab;
Lb=Psib/Ib;
kd=1.0084;
Mb=kd*PN/OmegaN;
Pb=Mb*Omegarb;
rs=Rs/Zb;
ls=Xs/Zb;
rr=Rr/Zb;
lr=Xr/Zb;
lm=Xm/Zb;
Tj=J*Omegarb/Mb;
betaN=(Omega0N-OmegaN)/Omega0N;
wN=(1-betaN);
SsN=3*UsN*IsN;
zetaN=SsN/Pb;
ks=lm/(lm+ls);
kr=lm/(lm+lr);
lbe=ls+lr+ls*lr*lm^(-1);
roN=0.9962;
rrk=roN*betaN;
alphar=kr*rr/lm;
le=kr*lbe;
re=rs+(kr^2)*rr;
Te=le/re;
Tr=(lm+lr)/rr;
Us=1;
ws=1;
t=2.5;
usa=Us*cos(ws*t);
usb=Us*cos(ws*t-2*pi/3);
usc=Us*cos(ws*t+2*pi/3);
us_alpha=(1/3)*(2*usa-usb-usc);
us_beta=1/(sqrt(3))*(usb-usc);
Литература:
-
Емельянов А.А., Бесклеткин В.В., Авдеев А.С., Чернов М.В., Киряков Г.А., Габзалилов Э.Ф., Фуртиков К.А., Реутов А.Я., Королёв О.А. Математическая модель асинхронного двигателя с переменными
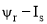в произвольной системе координат на основе интегрирующих звеньев // Молодой ученый. - 2015. - № 15. - С. 7-30.
- Шрейнер Р.Т. Электромеханические и тепловые режимы асинхронных двигателей в системах частотного управления: учеб. пособие / Р.Т. Шрейнер, А.В. Костылев, В.К. Кривовяз, С.И. Шилин. Под ред. проф. д.т.н. Р.Т. Шрейнера. - Екатеринбург: ГОУ ВПО «Рос. гос. проф.-пед. ун-т», 2008. - 361 с.
- Шрейнер Р.Т. Математическое моделирование электроприводов переменного тока с полупроводниковыми преобразователями частоты. - Екатеринбург УРО РАН, 2000. - 654 с.
