Целью работы является создание метода моделирования, который использовал бы преимущества математического аппарата нечёткой логики.
Пусть модель биологического процесса включает ряд показателей, изменяющихся во времени(t). Показатели {Xi(t)} являются входными для модели, показатели {Pi(t)} являются системными и зависят не только от t и {Xi(t)}, но и от других показателей. Один из показателей этого типа — Z(t) — является целевым для данной модели. Все показатели могут иметь два представления — в форме функции gj(t), которая отображает теоретические знания и задаётся дифференциальным уравнением, и в форме функции yj(t), которая задаётся уравнением регрессии. Примем, что: Pj=({gj(t)},{yj(t)}):
fgj({gi(t),i≠j}, {gi’(t) }, {gi’’(t) })=0; yj(t)=fyj(t, ξ,{Xi(t),Dyji}). (1)
Предлагаемый метод направлен на то, чтобы создать для Z(t) (Z(t)=Pj0(t)) динамическое нечёткое представление на Универсальном множестве гипотетических функций {gj0(t)}, используя при этом имеющую биологическое обоснование зависимость между Pj0(t) и Py0(t) — показателем, допускающим возможность статистического моделирования в форме альтернативных регрессионных уравнений. Определим два универсума (E1 и E2) и матрицу нечёткого вывода R. Элементом e1 множества E1 является функция yi(t, ξ, {Xk(t),Dyik}). Элементом e2 множества E2 является функция gj(t). Элемент матрицы нечёткого вывода Rij соответствует вероятности того, что из всех функций, определённых на случайном входе X, наблюдённое значение Zy(X) будет наилучшим образом приближаться функцией yi, при условии, что Z(X) лучше всего приближается функцией gj. Предлагаем алгоритм расчёта {Rij} по обучающей выборке. На множестве {tk} вычисляются статистические оценки функций y –ys — и g –gs. Тогда:
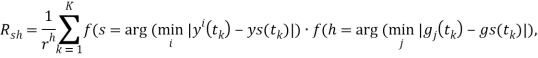(2)
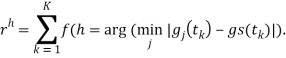f(true)=1, f(false)=0) (3)
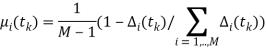, где 
(4)
Одна итерация включает измерение входных показателей (X0), последовательный расчёт системных показателей и сравнение Z(X0) с наблюдённым значением целевой функции. При значительном расхождении — корректировка модели. Последовательно вычисляются: yi(X0), Rij, µiи далее µjи c помощью процедуры дефазификации — прогнозируемое значение Z(X0).
Применим предложенный метод для разработки модели взаимосвязи двух факторов роста малоинвазивной опухоли по результатам, полученным в [1]. В [1] опухоль рассматривается как колония клеток, находящихся в состояниях: пролиферирующие клетки с плотностью n1(t), мигрирующие клетки и мёртвые клетки. Интенсивность перехода из одного состояния в другое зависит от концентрации глюкозы S(t). S(t) является фактором роста n1(t), а n1(t) — фактором снижения S(t). С учетом этих и других данных взаимосвязи для клеток опухоли описываются в [1, с.366–367] системами дифференциальных уравнений. Используя полученные в [1] уравнения, можно заключить, что, если S зависит от t логарифмически, то n1(t) при дополнительных допущениях принимает форму полинома:
, S(t)=Dlog(t), (5)
Чем меньше t и S(t), тем ближе зависимость n1(t) к полиному и меньше скорость роста, а увеличение t делает рост n1(t) экспоненциальным. Проблема заключается в численном определении коэффициентов. Традиционный путь состоит в том, чтобы увеличивать точность модельных функций включением всё новых факторов. Концепция нечёткой логики предполагает иной подход. В качестве функции, которая эмулирует динамический ряд значений S(t), был использован логарифм, функции, эмулирующей наблюдённые значения Z(t), — полином. Модельные функции:
Z(t)=0,002 t 4–0,22t3 + 7,05 t 2–55 t + 275, S(t)=250ln(t), (6)
g1(t)= -1,43 t2 +79,17t — 489,47, g2(t)= 0,0225e0,169t, y1(t)=16,5t+365, y2(t)= 8,4t + 584. (7)
По данным выборки была построена матрица нечёткого вывода R. Результаты контрольной прогонки показали χ2=33,2 при n=50, что меньше, чем χ2 n=50,α=0,05=67,5.
Обратимся к другому примеру. В [2] рассматривается вопрос влияния изменений цитокинового статусаи других факторов на прогрессирование хронической сердечной недостаточности (ХСН) ишемического генеза. Доказывается, например, что ФНО-α при превышении 5пг/мл приводит к высоким цифрам риска развития ХСН. Зависимость выражена логистической функцией [2, с.7]:
y=exp(-1,3449+0,266066x)/(1+exp(-1,3449+0,266066x)). (8)
Нетрудно заметить, что риск ХСН зависит от ФНО-α на отрезке от нуля до 12 линейно. Однако далее точность линейной аппроксимации снижается, и на отрезке от нуля до 14.5 χ2 n=15=64, т. е. расхождение велико. Дополним набор модельных функций нечёткой модели ещё одной регрессией. Теперь имеем y1(t)=0,089t+0,18; y2(t)=0,018t+0,75. Поскольку значения параметров позволяют ограничиться линейной аппроксимацией, то в данном частном случае gi(t)=yi(t), матрица нечёткого вывода — единичная. Точность модели χ2 n=15=12. Отметим, ещё одно преимущество нечёткой модели: и проще и эффективное исследовать зависимость параметров уравнения от других факторов для линейной функции, чем для логистической.
Покажем, что функциональная модель может быть представлена в форме нечёткой и наоборот. Располагая функциональной моделью, можно построить нечёткую модель, действуя по очевидному принципу. Но возможен и обратный переход. Представим альтернативные функции gj частными случаями функции fdc параметрами Ck, значения которых получаем решением задачи оптимизации:
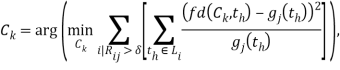(9)
где δ — константа, Li ={th| E j0| µj0=Rij0 или µj0= µi).
В заключение заметим, что широкое распространение методов мягких вычислений свидетельствует о практической значимости данного математического аппарата в компьютерном моделировании.
Литература:
- Колобов А. В., Кузнецов М. Б. Математическое моделирование роста малоинвазивной опухоли с учётом инактивации антиангиогенным препаратом фактора роста эндотелия сосудов //Компьютерные исследования и моделирование. 2015 г. Т. 7. № 2. С. 374–381.
- Яровова Е. С., Кастанаян А. А., Иванов И. В. Влияние иммунного воспаления на прогрессирование хронической сердечной недостаточности ишемического генеза // Современные проблемы науки и образования. — 2012. — № 4;
- URL: www.science-education.ru/104–6641 (дата обращения: 17.10.2015).
