Condition of a suspension bracket of the car — the characteristic directly influencing traffic safety. Especially fixed control is necessary behind a condition of a suspension bracket of dump trucks, tractors — often they transport freight weighing over 10 tons on roads not of the best quality that directly affects decrease in reliability of a suspension bracket and can lead to a road accident. For decrease in a share of a human factor in definition of a working order of elastic elements of a suspension bracket of the truck, and also for increase in capacity of posts of daily service use of the robot providing control of a condition of a suspension bracket of the car is offered.
Keywords: diagnostics of the truck, maneuverable chassis, ultrasound, manipulator, optimum trajectory of the manipulator.
Робот для определения технического состояния подвески автомобиля спроектирован на колесном шасси, которое обеспечивает маневренность и хорошую проходимость робота, а также скорость перемещения [1].
На роботе установлен манипулятор, выполняющий следующие функции:
датчик ультразвука позволяет обнаружить микротрещины в подвеске автомобиля: рессорах, рычагах, стяжках, реактивных тягах, а также в раме.
камера, установленная на манипуляторе, обеспечивает передачу изображения, позволяет визуально оценить состояние амортизаторов либо жидкости из системы охлаждения, подтекание смазки из картеров мостов, состояние пневмобаллонов подвески.
светодиодный фонарь обеспечивает освещение диагностируемых элементов.
Определенную трудность вызывает формирование правильной траектории манипулятора для точного его позиционирования в пространстве.
Проблема формирования оптимальной траектории может быть сформулирована как задача оптимального управления [2]. Для динамической системы
![]() (1)
(1)
сначальным состоянием ![]() и конечным состоянием
и конечным состоянием ![]() при заданном или свободном времени окончания процесса требуетсянайти управление
при заданном или свободном времени окончания процесса требуетсянайти управление ![]() и соответствующее состояние
и соответствующее состояние ![]() , оптимизирующие показатель качества
, оптимизирующие показатель качества
![]() (2)
(2)
При планировании оптимальных траекторий движенияманипулятора используются уравнения кинематики
![]() (3)
(3)
и динамики
![]() (4)
(4)
где p — вектор, представляющий положение рабочего органа манипулятора в декартовой системе координат; q — вектор, представляющий перемещения в степенях подвижности манипулятора. В качестве управления u рассматриваются развиваемые приводами в степенях подвижности силы и моменты. Начальное состояние определяется равенствами
![]() (5)
(5)
и
В конечный момент
![]() (7)
(7)
и
![]() (8)
(8)
Ограничения вида равенств
![]() (9)
(9)
определяют требуемую геометрическую траекторию. Ограничения вида неравенств устанавливают пределы изменения развиваемых приводами сил (моментов) и скоростей:
![]() (10)
(10)
Для решения поставленной задачи предложено использовать метод динамического программирования. Такой подход позволяет получить универсальный алгоритм формирования оптимальных траекторий при различных ограничениях и показателях качества. Облегчает использование метода то обстоятельство, что при заданной геометрической траектории положение в одной степени подвижности определяет положения в остальных. В результате существенно снижается размерность задачи [3].
Пусть ![]() ˗ индекс дискретной точки на заданной геометрической траектории. Для заданного в декартовых координатах положения рабочего органа в точке k путем решения обратной задачи кинематики манипулятора можно определить соответствующие обобщенные координаты q(k). Пусть
˗ индекс дискретной точки на заданной геометрической траектории. Для заданного в декартовых координатах положения рабочего органа в точке k путем решения обратной задачи кинематики манипулятора можно определить соответствующие обобщенные координаты q(k). Пусть ![]() — множество возможных скоростей движения в степени подвижности i в точке k, которое получается путем дискретизации диапазона скоростей
— множество возможных скоростей движения в степени подвижности i в точке k, которое получается путем дискретизации диапазона скоростей
В том случае, когда ограничения скорости не указаны, ее предельные значения могут быть получены из ограничений сил (моментов). Рассмотрим переход манипулятора из точки k, в точку k + 1. Предполагается, что величина перемещения мала, а ускорение постоянно. Для возможной скорости ![]() и допустимой скорости
и допустимой скорости ![]() ускорение движения в сочленении i в точке k определяется выражением:
ускорение движения в сочленении i в точке k определяется выражением:
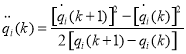 (12)
(12)
и время перехода между двумя точками
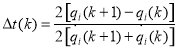 (13)
(13)
Поскольку перемещение в следующую точку для всех степеней подвижности должно завершаться за один и тот же временной интервал, можно определить скорости движения в остальных степенях подвижности в точке k как:
![]() (14)
(14)
Если какая-либо из скоростей ![]() не удовлетворяет ограничениям для скоростей, то скорость
не удовлетворяет ограничениям для скоростей, то скорость ![]() считается недопустимой. Если же все скорости удовлетворяют ограничениям, то для каждой степени подвижности вычисляется ускорение. Далее по полученным значениям перемещений, скоростей и ускорений вычисляются силы (моменты), которые необходимо приложить в степенях подвижности для выполнения перемещения из точки k в k+1. Если при этом оказывается, что какая-либо из сил (моментов) выходит за допустимые пределы, то скорость
считается недопустимой. Если же все скорости удовлетворяют ограничениям, то для каждой степени подвижности вычисляется ускорение. Далее по полученным значениям перемещений, скоростей и ускорений вычисляются силы (моменты), которые необходимо приложить в степенях подвижности для выполнения перемещения из точки k в k+1. Если при этом оказывается, что какая-либо из сил (моментов) выходит за допустимые пределы, то скорость ![]() также полагается недопустимой [3].
также полагается недопустимой [3].
Пусть ![]() обозначает приращение показателя качества при перемещении между точками k и k + 1 и
обозначает приращение показателя качества при перемещении между точками k и k + 1 и ![]() обозначает наименьшее значение показателя качества при переходе из k — той точки в конечное состояние. Используя принцип оптимальности Беллмана, можно получить:
обозначает наименьшее значение показателя качества при переходе из k — той точки в конечное состояние. Используя принцип оптимальности Беллмана, можно получить:
![]() (15)
(15)
где ![]() — множество допустимых скоростей в точке k+1. Это уравнение применяется к каждой допустимой скорости в точке k и позволяет для каждой скорости найти единственную оптимальную скорость в точке k + 1 и скорости в остальных степенях подвижности, а также силы (моменты), соответствующие оптимальным условиям в точке k. Оптимизационный процесс начинается в конечном состоянии и распространяется в направлении начала [1].
— множество допустимых скоростей в точке k+1. Это уравнение применяется к каждой допустимой скорости в точке k и позволяет для каждой скорости найти единственную оптимальную скорость в точке k + 1 и скорости в остальных степенях подвижности, а также силы (моменты), соответствующие оптимальным условиям в точке k. Оптимизационный процесс начинается в конечном состоянии и распространяется в направлении начала [1].
В статье рассмотрен способ задания оптимальной траектории манипулятора в пространстве посредством динамического программирования. Именно этот метод позволяет учесть значения скоростей звеньев манипулятора, а так же вычислить их ускорения. С учетом ускорения становится возможным найти силы и моменты этих сил.
Литература:
- Поезжаева Е. В. Промышленные роботы: учеб.пособие: в 3ч. / Е. В. Поезжаева. — Пермь: Изд-во Перм. гос. тех. ун-та,2009. — Ч.2. — 185 с.
- Проблемы механики современных машин: Материалы V международной конференции. — Улан-Удэ: Изд-во ВСГУТУ, 2012. — Т. 3. — 276с., ил. — Поезжаева Е. В., «Шагающий робот с контурной системой управления», с.227.
- Поезжаева Е. В., Васенин А. С., Шумков А. Г. Роботизация фермерских хозяйств по обработке растений // Вестник Восточно-Сибирского государственного университета технологий и управления. 2014. № 3. С. 59–62.







