Токарная обработка вязких и мягких материалов на большой скорости характеризуется образованием сливной стружки, которая в значительной степени влияет на процесс резания, снижает производительность процесса обработки и стойкость инструмента, ухудшает качество обработанных поверхностей, затрудняет многостаночное обслуживание и является носителем повышенной опасности при работе на токарных станках, что вызывает необходимость ее дробления на мелкие элементы. Решению задачи дробления стружки, получения ее в виде отрезков посвящен ряд исследований [1,2].
Обеспечить дискретный режим стружкодробления позволяет использование привода подач токарного модуля с фрикционной механической передачей (ФМП) [1]. Существенной особенностью привода является наличие в нем фрикционной механической передачи, в которой применены две цилиндрические фрикционные пары и две пары ролик-шток (рис. 1)
Возможность упрощения расчетных механических схем подчиняется общему правилу: основные закономерности движения многомассовых упругих механических систем определяются наибольшими массами и наименьшими жесткостями связей систем. Проведенный в [5] анализ динамики привода подачи с многоступенчатой ФМП показал, что передаточная функция привода достаточно сложна
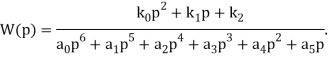 (1)
(1)
В результате обоснованного приведения сил, приложенных к разным звеньям, к одной, приложенной к звену приведения, а также замены массы всех звеньев механизма на условную приведенную массу, связанную со звеном приведения, стало возможным решение динамической задачи исследования движения механизма как звена приведения (ведущего звена).
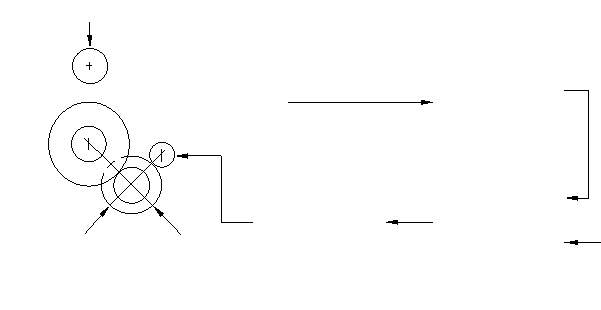
Рис. 1. Схема привода с фрикционной механической передачей:
О0..О3 – ролики ФМП, Р1..Р3 – силы прижима роликов
Динамическая модель привода подачи токарного модуля можно представить в виде одномассовой модели, нагруженной ступенчато изменяющейся силой резания.
По полученным в [1] значениям подачи и рассчитанным продолжительностям разгона, равномерного движения и торможения, обеспечивающим дробление стружки, были смоделированы трапециидальный, синусоидальный и колоколообразный законы управления кареткой.
Полученный гармонический спектр трапецеидального, синусоидального и колоколообразного законов перемещения каретки представлен на рис. 2.
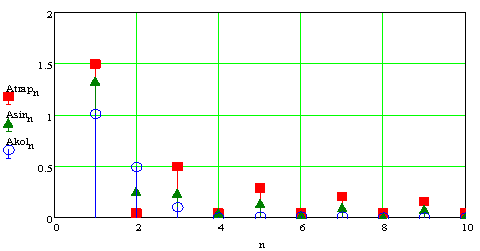
Рис. 2. Амплитудные спектры трапецеидального, синусоидального
и колоколообразного законов перемещения каретки
Из рисунка видно, что для трапецеидального сигнала значимыми являются первая, третья, пятая и седьмая гармоники, в то время как для заданных синусоидального и колоколообразного – первая и вторая гармоники. Плавное изменение формы сигнала требует меньшее число гармоник при той же точности представления, чем скачкообразный сигнал. Амплитуда первой гармоники у сигнала трапецеидальной формы больше, чем у сигнала синусоидальной и колоколообразной формы, из чего можно сделать вывод, что величина перерегулирования в этом случае будет больше, чем у двух других. С точки зрения теории автоматического управления это не является оптимальным вариантом.
Таким образом, используя полученные результаты, можно смоделировать прохождение полученного сигнала через колебательное звено, которое представляет собой привод подач с ФМП, и определить показатели качества процесса управления.
Литература:
- Виноградов М.В. Управление приводом подачи токарного станка в режиме стружкодробления // Автоматизация и управление в машино- и приборостроении: сб. науч. тр. Саратов: СГТУ, 2014. С. 18-26.
- Лавров Н.К. Завивание и дробление стружки в процессе резания. М.: Машиностроение, 1971. 239 с.







