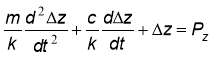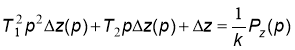)
Для создания системы управления процессом резания и анализа её работы необходимо построить математические модели всех её элементов. Сам процесс резания - наиболее сложный элемент системы. Он состоит из множества взаимодействующих друг с другом составляющих, и его моделирование связано с существенными трудностями. Одним из возможных способов построения модели является анализ физических процессов при резании [1].
В процессе резания возникают следующие силы: сила резания, вызывающая деформацию инструмента и заготовки, сила упругости, возникающая в результате взаимодействия атомов твёрдого тела при их выходе из положения равновесия, силы трения стружки о резец и резца о заготовку и др. [2].
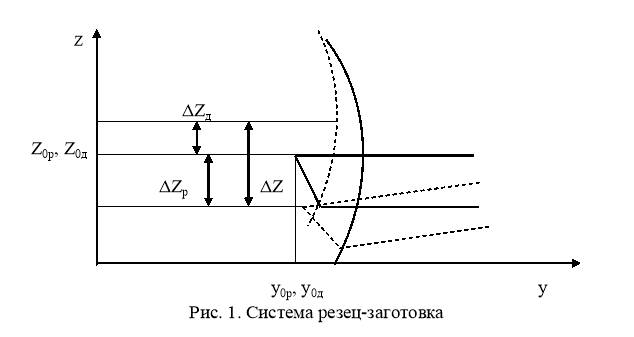
Рассмотрим систему резец-заготовка в системе координат (y, z), связанной с точкой пространства, на которую работа станка не может оказывать влияние (Рис. 1). Обозначим положение резца и заготовки до врезания координатами (yр0, zр0) и (yд0, zд0) соответственно. В процессе резания резец и заготовка деформируются и принимают положения, обозначенные координатами (yр0+Δyр, zр0-Δzр) и (yд0-Δyд, zд0+Δzд).
Рассмотрим движения системы резец-заготовка вдоль оси z [1]. Согласно второму закону Ньютона, дифференциальное уравнение движения тела представляет собой произведения массы тела на его ускорение:
|
|
( 1) |
,
где F – равнодействующая сил, действующих на тело, m - масса тела, а – ускорение тела.
Для случая упругих колебаний, возникающих в процессе резания, уравнение движения вдоль оси z в первом приближении можно записать так:
|
|
( 2) |
,
где Pz – тангенциальная сила резания, 
– сила трения резца о заготовку, препятствующая колебаниям, с - коэффициент демпфирования, kΔz - сила упругости, k - коэффициент упругости.
Перепишем (2) в виде:
|
|
(3) |
,
Разделим обе части уравнения на k, чтобы привести коэффициент при Δz к единице:
|
|
(4) |
имеет размерность квадрата времени, так что 
имеет размерность времени, так что
В преобразованиях Лапласа:
|
|
(5) |
Для представления модели в стандартном виде удобно заменить коэффициент жёсткости k на коэффициент податливости 
|
|
(6) |
Таким образом, передаточная функция будет равна:
|
|
(7) |
В процессе резания колеблются системы резца и заготовки. Для каждого из этих элементов упругой системы справедливы вышеприведённые рассуждения. Тангенциальная сила резания действует на заготовку со стороны резца. Согласно третьему закону Ньютона, заготовка будет действовать на резец с силой, равной по модулю и противоположной по направлению. Считая каждую из двух тангенциальных сил резания положительной в обоих моделях, можно определить относительное смещение резца и заготовки как Δzp+Δzд. Несмотря на то, что заготовка и резец колеблются в разных фазах, эта запись с учётом знаков будет сохранять справедливость в любой момент времени. Тогда модель рассматриваемой упругой системы будет иметь вид, показанный на рисунке 2.
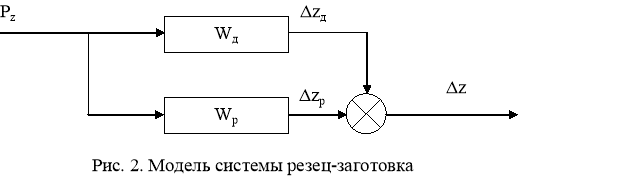где 
- математическая модель упругой системы резца,
Kp - коэффициент податливости резца, 
- математическая модель упругой системы заготовки, Kд - коэффициент податливости заготовки.
В физике при разложении равнодействующей силы на составляющие, каждая составляющая считается независимой, и ни одна из сил не может оказывать непосредственного влияния на другую. Pz – сила, возникающая в результате сопротивления твёрдого тела - заготовки внедрению другого твёрдого тела - резца - и снятию с неё стружки. Эта сила зависит только от смещения Δz и от таких параметров, как твёрдость материала резца и заготовки, углов резания, колебания припуска и т.д., которые мы на данном этапе не рассматриваем. При внедрении резца в заготовку, атомы заготовки смещаются с положения равновесия и в заготовке возникает напряжённое состояние, проявляющееся в возникновении силы. Чем больше глубина резания, тем больше атомов вовлечены в процесс и тем больше возникающая сила сопротивления. Объём срезаемой стружки не будет связан с величиной Δz линейной зависимостью. Однако, пределы, в которых изменяется Δz, очень малы. Геометрически можно определить связь Δzc изменением глубины резания Δt. Диапазон её изменения так же будет мал. Считая зависимость тангенциальной силы резания Pz от глубины резания t линейной в данном диапазоне, можно представить передаточную функцию, связывающую Δz с изменением тангенциальной силы резания ΔPz в виде безынерционного звена W=e, где e - коэффициент, равный 
. Тогда модель замкнутой упругой системы будет выглядеть следующим образом - рисунок 3.
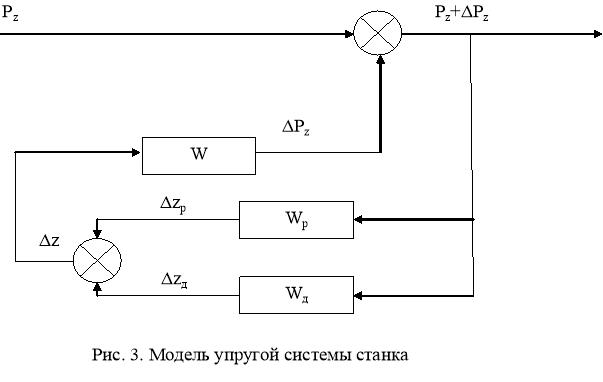
В работе была получена математическая модель деформации системы деталь-заготовка, учитывающая относительное перемещение резца и заготовки и их влияние на силу резания. Как видно из схемы, колебания резца и заготовки влияют на выходное значение силы резания. По модели, аналитически, можно установить, что колебания резца и заготовки будут влиять на геометрические параметры детали.
Литература:
1. Кудинов В. А. Динамика станков // М., Машиностроение, 1967.
2. Ящерицын П. И. Основы резания материалов и режущий инструмент. – 1981.
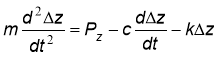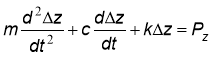