Построение математической модели упругой системы станка

 

В данной работе ставится задача идентификации математической модели, которая описывает колебания сил резания при точении [2]. На рис.1 представлен график изменения силы резания в процессе точения.

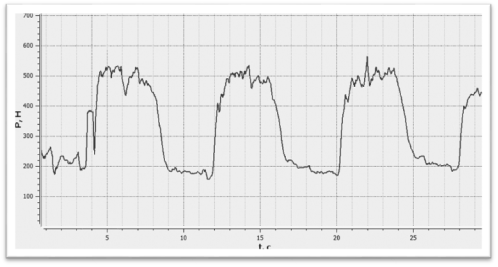
Рис.1. Изменение силы резания при точении

На графике видно, что кривая изменения силы резания имеет экспоненциальный вид с наложенной переменной составляющей силы резания. Наличие этой составляющей обусловлено упругостью системы. Для исследования природы переменной составляющей (в работе [1]) была получена аналитическая модель упругой системы станка, учитывающая относительное перемещение резца и заготовки в процессе резания. Данная модель представлена на рис.2.

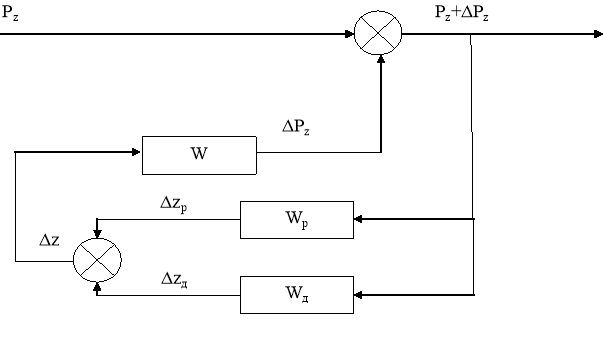
Рис.2. Модель системы резец-заготовка

Модель упругой системы станка имеет следующую передаточную функцию:

(1)

Идентификацию модели проведем на основе данных, полученных в результате эксперимента. Данный эксперимент заключался в ударном воздействии на заготовку и исследовании отклика с помощью акселерометра. При этом заготовка была поджата обратной стороной резца (для исключения поломки режущей пластины) с силой, соответствующей номинальной силе резания при заданных режимах резания.

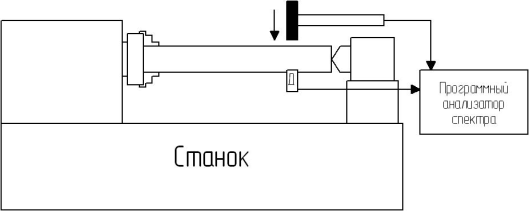
Рис.3. Схема эксперимента по снятию частотных характеристик

В ходе эксперимента были получены следующие амплитудно-частотные характеристики упругой системы станка:

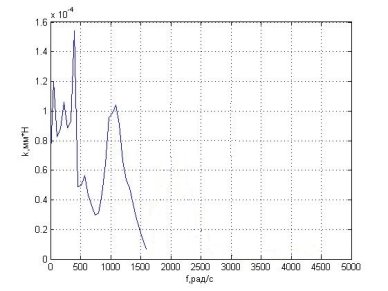
Рис.4. АЧХ экспериментальной модели

Модель, полученная аналитическим путем, должна иметь аналогичные частотные характеристики.

Для нахождения характеристик была составлена программа поиска оптимальных коэффициентов математической модели упругой системы станка в Matlab, текст которой приведен ниже:

loaddata20A5.mat% загрузка данных

X=[ 1 1 1 1 1 1]%задание начальных значений коэффициентов

options=optimset('display','iter');%задание опций для функции поиска коэффициентов

X=fminsearch('koleb',X,options,A,f);% задание функции подбора оптимальных коэффициентов

functionf=koleb(X,A,f); % создание файла функции

K=X(1); % ввод начальных коэффициентов

T2=X(2);

T1=X(3);

K2=X(4);

T22=X(5);

T21=X(6);

Wk=10; % ввод моделей звеньев системы

W1=tf([K],[T2 T1 1]);

W2=tf([K2],[T22 T21 1]);

W6=feedback(W1,Wk); % соединение элементов обратной связью

W5=feedback(W2,Wk);

W=W5+W6;

[mag, phase] = bode(W,f); % расчет векторов амплитуд и фаз частотной характеристики

mag=(mag(1,:))'; % построениеАЧХ

figure(2)

plot(f,mag,'r',f,A)

f=(sum(abs(A-mag)); % критерий подбора коэффициентов

 

В результате были получены передаточные функции звеньев исследуемой модели:

(2)

На рис.4 изображены частотные характеристики обоих моделей.

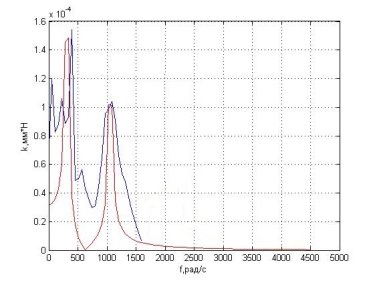
Рис.4. АЧХ экспериментальной и аналитической моделей

Модель, полученная аналитическим путем, с достаточной точностью описывает экспериментально снятую АЧХ упругой системы станка. Это обосновывает дальнейшее изучение данной модели для использования ее при построении систем управления процессом резания.

 

Литература:

1. Кудинов В. А. Динамика станков // М., Машиностроение, 1967.