В работе представлены результаты математического моделирования теплопереноса в полуограниченном теле с целью определения конструктивных и режимных характеристик измерительного устройства (измерительного зонда — ИЗ), предназначенного для реализации метода теплового неразрушающего контроля (НК) структурных переходов в полимерных материалах (ПМ).
Математическое моделирование в настоящее время получило широкое распространение для оптимизации сложных процессов и различных измерительных систем. Это связано с тем, что для определения искомых параметров необходимо проводить долгие и дорогостоящие эксперименты. Математическое моделирование позволяет снизить затраты на проведение экспериментов и исключить ошибки проектирования сложных систем [1–3].
Известны методы и реализующие их измерительные системы, позволяющие осуществлять НК теплофизических свойств и температурных характеристик структурных переходов в полимерных материалах [4–7].

Рис. 1. Измерительная схема метода: 1 — подложка ИЗ; 2 — нагреватель Н1; 3 — нагреватель Н2; 4, 5, 6 — ТП1, ТП2, ТП3; 7 — исследуемое изделие
В данной работе рассматривается тепловой метод НК, измерительная схема которого представлена на рис.1. Тепловое воздействие на исследуемое полимерное тело, имеющее равномерное начальное температурное распределение, осуществляется с помощью двух линейных нагревателей постоянной мощности, встроенных в подложку ИЗ. Начальное температурное распределение контролируется одновременно тремя термоэлектрическими преобразователями (ТП1 — ТП3), расположенными на поверхности подложки ИЗ. ТП1 расположен на центральной оси контактной поверхности подложки ИЗ. ТП2 и ТП3 находятся на расстояниях х´ по обе стороны от оси (на центральных линиях нагревателей). В ходе эксперимента фиксируются зависимости избыточной температуры ТТП1, ТТП2, ТТП3 от времени, а также значения разностей значений температуры на нагревателях и в точке, расположенной на центральной оси контактной поверхности подложки ИЗ.
Тепловая схема метода представлена на рис. 2. В начальный момент времени температура тела во всех точках пространства одинакова и равна нулю. В момент времени τ = 0 на поверхности тела начинают действовать два источника постоянной мощности с линейной мощностью q0 каждый, обладающие удельной теплоемкостью сн. При температуре T = Tп материал 1 имеет фазовый переход (ФП), сопровождающийся тепловым эффектом ![]() .
.
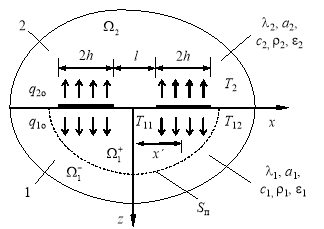
Рис. 2. Тепловая схема: 1 — исследуемое изделие; 2 — подложка ИЗ
Введем обозначения: ![]() ,
, ![]() – распределения температуры в исследуемом изделии в первой и второй фазах, соответственно;
– распределения температуры в исследуемом изделии в первой и второй фазах, соответственно; ![]() описывает температурное поле в пределах области
описывает температурное поле в пределах области ![]() , а
, а ![]() — температурное поле в пределах области
— температурное поле в пределах области ![]() , где
, где ![]() температура фазового перехода, который происходит на границе раздела двух фаз
температура фазового перехода, который происходит на границе раздела двух фаз ![]() (разделяет расчетную область
(разделяет расчетную область ![]() на две подобласти:
на две подобласти: ![]() и
и ![]() , в первой из которых температура превышает температуру ФП, а во второй — не превышает; T1, T2, a1, a2, 1, 2, ε1, ε2, ρ1, ρ2 — значения избыточной температуры, ˚С; температуропроводности, м2/с; теплопроводности, Вт/(м∙˚С); тепловой активности, Вт∙с0,5/(м2∙˚С); плотности материалов, кг/м3, исследуемого изделия и подложки ИЗ, соответственно.
, в первой из которых температура превышает температуру ФП, а во второй — не превышает; T1, T2, a1, a2, 1, 2, ε1, ε2, ρ1, ρ2 — значения избыточной температуры, ˚С; температуропроводности, м2/с; теплопроводности, Вт/(м∙˚С); тепловой активности, Вт∙с0,5/(м2∙˚С); плотности материалов, кг/м3, исследуемого изделия и подложки ИЗ, соответственно.
Математическая форма задачи:
![]() ,
, ![]() ;(1)
;(1)
![]() ,
, ![]() ;(2)
;(2)
![]() ,
, ![]() ;(3)
;(3)
![]() ;(4)
;(4)
![]() ;(5)
;(5)
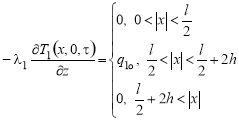 ;(6)
;(6)
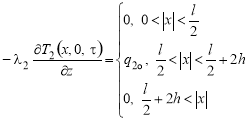 ;(7)
;(7)
![]() ;(8)
;(8)
![]() ,
, ![]() ;(9)
;(9)
![]() ,
, ![]() ;(10)
;(10)
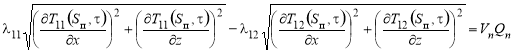 ;(11)
;(11)
![]() ;(12)
;(12)
![]() ,
, ![]() .(13)
.(13)
где 11, 12 — теплопроводность исследуемого изделия до ФП и после соответственно, Вт/(м∙˚С); 2h — ширина нагревателя, м; l — расстояние между нагревателями, м; ![]() — скорость движения границы ФП, ˚С/мин;
— скорость движения границы ФП, ˚С/мин; ![]() — теплота, поглощенная (выделившаяся) при ФП, Вт;
— теплота, поглощенная (выделившаяся) при ФП, Вт; ![]() — мощность, выделяющаяся на единицу длины нагревателя, Вт/м;
— мощность, выделяющаяся на единицу длины нагревателя, Вт/м; ![]() ,
, ![]() ,
, ![]() — части мощности, идущие на нагрев исследуемого изделия, материала подложки ИЗ и разогрев нагревателя соответственно, Вт/м.
— части мощности, идущие на нагрев исследуемого изделия, материала подложки ИЗ и разогрев нагревателя соответственно, Вт/м.
Решение задачи (1) — (13) получено с учетом ряда допущений, подробно представленных в работе [8].
Распространение тепла в исследуемом полуограниченном теле, в предположении отсутствия ФП, получено по принципу суперпозиции на основании известных ранее решений [8]:
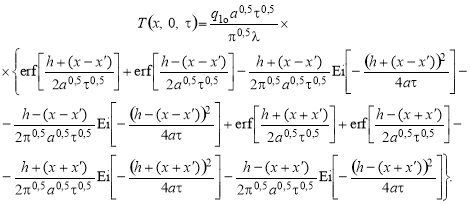 (14)
(14)
где τ — время, с; х — координата, м; х´ — расстояние от центра измерительного зонда до середины нагревателя, м; λ — теплопроводность, Вт/м∙ºС; а — температуропроводность, м2/с.
После ряда преобразований получено выражение для температуры поверхности z = 0 в точке с координатой x для больших значений [2, 3]:
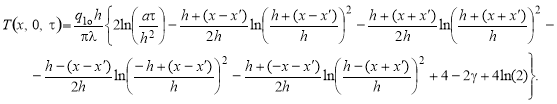 (15)
(15)
где γ — число Эйлера.
Решения (14) и (15) использованы для оптимизации конструктивных и режимных характеристик ИЗ, предназначенного для реализации теплового метода НК структурных переходов в ПМ.
Выражение для определения перепада значений температуры ∆Т,между точками контроля расположенными на центральной оси контактной поверхности подложки ИЗ и на центральных линиях нагревателей (при х = 0), имеет вид:
![]() (16)
(16)
где ![]() — температура на нагревателе, °С;
— температура на нагревателе, °С; ![]() — температура на центральной оси между нагревателями, °С.
— температура на центральной оси между нагревателями, °С.
Проведя ряд преобразований с использованием (15) и (16) получено выражение позволяющее определить величину теплового потока, который подает в материал каждый нагреватель.
![]() ,(17)
,(17)
где p — переменная, отражающая конструктивные особенности ИЗ
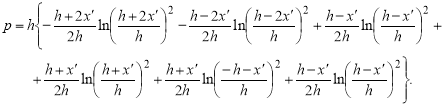 (18)
(18)
Выполнив аналогичные преобразования с (14) и (15) получено выражение позволяющее определить действительный ∆Т между центральной осью контактной поверхности подложки ИЗ и центральной линией нагревателей:
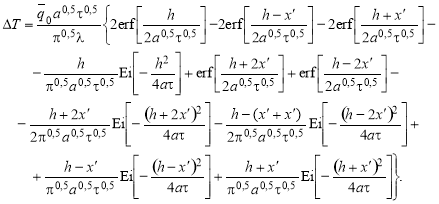 (19)
(19)
Из конструктивных соображений ширина каждого нагревателя равняется 2,2 мм. Введем условие, что перепад значений температуры ΔТ между центральной осью контактной поверхности подложки ИЗ и центральной линией нагревателей, будет изменяться в пределах 3... 10 ºС.
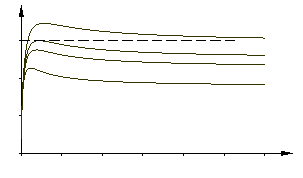
На рис. 3 построены зависимости перепада значений температуры от времени при различных расположениях нагревателей от центральной оси контактной поверхности подложки ИЗ. Из представленного следует, что оптимальным расстоянием от центральной оси контактной поверхности подложки ИЗ до середины нагревателя x' = 2,7 мм.
|
|
|
|
а) |
б) |
Рис. 3. Зависимости перепада значений температуры от времени при различных расположениях нагревателей. Изделие из ПММА: а) ∆Т = 3 ºС; б) ∆Т = 10 ºС. 1) x'=2,0 мм; 2) x'=2,5 мм; 3) x'=2,7 мм; 4) x'=3,0 мм.
Величину теплового потока, воздействующего на полуограниченное тело, следует назначать в зависимости от значения теплопроводности, перегрева исследуемого изделия и принятого перепада значений температуры. Причем, во-первых, для наименьшего перегрева исследуемого изделия величину ΔT следует назначать равной 3 °С, а для наиболее теплопроводных материалов величину перегрева следует назначать 10 °С. Величина переменной, отражающей конструктивные особенности ИЗ, р = 0,00254.
Таким образом, для системы, состоящей из двух нагревателей шириной 2,2 мм каждый, оси которых расположены на расстоянии 5,4 мм друг от друга, для достижения заданного ∆Т = 3... 10 °С, в зависимости от перегрева исследуемого изделия и значения теплопроводности ПМ, величину теплового потока воздействующего на полуограниченное тело, следует назначать в интервале значений 742... 9890 Вт/м2.
Литература:
- Жуков, Н. П. Моделирование процесса теплопереноса от импульсного линейного источника тепла при теплофизических измерениях / Н. П. Жуков // Инженерно-физический журнал. — 2005. — Т.78, № 3. — С.86–95.
- Жуков, Н. П. Моделирование оттоков тепла в зонд при теплофизическом контроле / Н. П. Жуков // Инженерно-физический журнал. — 2005. — Т.78, № 4. — С.108–116.
- Математическое моделирование теплопереноса от двух нагревателей в полуограниченном теле / Н. П. Жуков, Н. Ф. Майникова, И. В. Рогов, О. Н. Попов // Вестник Тамбовского государственного технического университета. — 2012. — Т. 18, № 2. — С. 327–332.
- Жуков, Н. П. Измерительно-вычислительная система неразрушающего теплофизического контроля / Н. П. Жуков, Н. Ф. Майникова // Приборы и техника эксперимента. — 2005. — № 2. — С. 153–154.
- Жуков, Н. П. Измерительно-вычислительная система неразрушающего контроля теплофизических свойств / Н. П. Жуков, Н. Ф. Майникова // Приборы и техника эксперимента. — 2005. — № 4. — С. 164–166.
- Майникова, Н. Ф. Измерительная система и метод неразрушающего контроля структурных превращений в полимерных материалах / Н. Ф. Майникова // Приборы и системы. Управление, контроль, диагностика. — 2006. — № 1. — С. 56–61.
- Майникова, Н. Ф. Измерительная система неразрушающего контроля структурных превращений в полимерных материалах / Н. Ф. Майникова // Приборы и системы. Управление, контроль, диагностика. — 2006. — № 9. — С. 45–48.
- Многомодельные методы в микропроцессорных системах неразрушающего контроля теплофизических характеристик материалов: учебное пособие / С. В. Мищенко, Ю. Л. Муромцев, Н. П. Жуков, Н. Ф. Майникова, И. В. Рогов, О. Н. Попов; под ред. С. В. Мищенко. — Тамбов: изд-во ФГБОУ ВПО «ТГТУ», 2012. — 112 с.