Широтно-импульсная модуляция — процесс управления мощностью, подводимой к нагрузке, путём изменения скважности импульсов, при постоянной частоте.
Напряжение переменного тока зависит от двух параметров: амплитуды и частоты. Важно контролировать эти два параметра. Наиболее эффективно контролировать эти параметры с помощью методов широтно-импульсной модуляции.
Метод пространственно-векторной широтно-импульсной модуляции один из самых популярных методов в последнее время (SVPWM) [2], [3]. Этот метод в результате дает более высокую величину выходного опорного напряжения по сравнению с синусоидальной ШИМ. Однако, метод пространственно-векторной широтно-импульсной модуляции использующийся в трехуровневых преобразователях более сложный из-за большого количества переключения состояний инвертера.
Пространственно-векторная широтно-импульсная модуляция
В пространственно-векторной широтно-импульсной модуляции выходное напряжение аппроксимируется с помощью трех выходных векторов, исходящих из углов треугольника, содержащего опорный вектор в пространственно-векторной диаграмме инвертора. Когда опорный вектор переходит из одной области в другую, он может вызвать резкое изменение выходного вектора. Кроме того, мы должны рассчитать переключающую последовательность и время переключения состояний при каждом изменении направления опорного напряжения.
Основным преимуществом этого метода является то, что он будет генерировать меньше гармонических искажений в выходных напряжении и токе [1].
Основной принцип предлагаемого метода SVPWM
В работе представлен простой и быстрый метод, который делит пространственно-векторную диаграмму пятиуровневого инвертора в две стадии на несколько небольших шестиугольников, каждый шестиугольник — это пространственно-векторная диаграмма двухуровневого инвертора.
Мы должны сделать два упрощения: во-первых, пространственно-векторная диаграмма пятиуровневого преобразователя состоит из шести пространственно-векторных диаграмм трехуровневого инверторы. Во-вторых, каждая из этих диаграмм для трехуровневого инвертора делится на шесть пространственно-векторных диаграмм инвертора второго уровня [1].
Первая коррекция вектора опорного напряжения
Зная местоположение заданного опорного вектора напряжения, выбираем один шестиугольник из шести небольших, которые содержат пространственно-векторную диаграмму пятого уровня на рис. 1. Там существуют некоторые области, которые перекрываются двумя соседними маленькими шестиугольниками. Эти области будут разделены поровну между двумя шестиугольниками, как показано на рис. 2. Каждый шестиугольник идентифицируется по количеству определенных S, как приведено в табл. 1
После выбора одного шестиугольника, мы делаем перемещение опорного вектора ![]() в сторону центра этого шестиугольника, как это показано на рис. 3. Это перемещение сделано путем вычитания центрального вектора выбранного шестиугольника от первоначального опорного вектора.
в сторону центра этого шестиугольника, как это показано на рис. 3. Это перемещение сделано путем вычитания центрального вектора выбранного шестиугольника от первоначального опорного вектора.
В таблице 3 даны компоненты D и Q опорного напряжения ![]() после перемещения для всех шести шестиугольников. Индекс (3) или (5) выше компоненты указывает на трех- или пятиуровневый случаи соответственно.
после перемещения для всех шести шестиугольников. Индекс (3) или (5) выше компоненты указывает на трех- или пятиуровневый случаи соответственно.
Таблица 1
Выбор шестиугольников в зависимости от угла
|
Шестиугольник «S» |
Расположение опорного напряжения вектором фазового угла « |
|
1 |
|
|
2 |
|
|
3 |
|
|
4 |
|
|
5 |
|
|
6 |
|
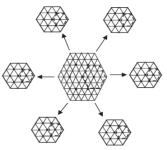
Рис. 1. Декомпозиция пространственно-векторной диаграммы пятиуровневого инвертора
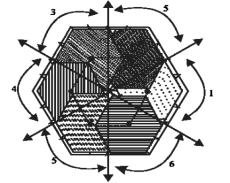
Рис. 2. Разделение пересекающихся областей
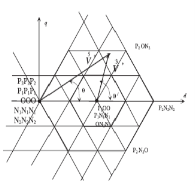
Рис. 3. Первый перенос вектора опорного напряжения
Вторая коррекция вектора опорного напряжения
Имеется выбранная схема инвертора третьего уровня, знаем расположение перемещенного вектора, выбран один шестиугольник среди шести небольших, которые содержат эту трехуровневую схему (рис. 4). Здесь также перекрывающиеся области поровну разделены между двумя шестиугольниками. После выбора одного шестиугольника, мы делаем перемещение опорного вектора ![]() по направлению к центру этого шестиугольника, как показано на рисунке 5.
по направлению к центру этого шестиугольника, как показано на рисунке 5.
Этот перевод сделан путем вычитания центрального вектора шестиугольника из исходного опорного вектора. В таблице 4 даны компоненты D и Q опорного напряжения ![]() после переноса для всех шести шестиугольников. Индекс (2) или (3) над компонентом указывает на двух- или трехуровневый случаи соответственно.
после переноса для всех шести шестиугольников. Индекс (2) или (3) над компонентом указывает на двух- или трехуровневый случаи соответственно.
Таблица 2
Первая коррекция вектора опорного напряжения
|
S |
|
|
|
1 |
|
|
|
2 |
|
|
|
3 |
|
|
|
4 |
|
|
|
5 |
|
|
|
6 |
|
|
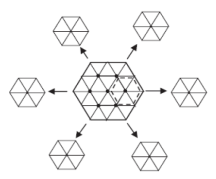
Рис. 4. Декомпозиция пространственно-векторной диаграммы трехуровневого инвертора на 6 шестиугольников
Таблица 3
Первая коррекция вектора опорного напряжения
|
S |
|
|
|
1 |
|
|
|
2 |
|
|
|
3 |
|
|
|
4 |
|
|
|
5 |
|
|
|
6 |
|
|
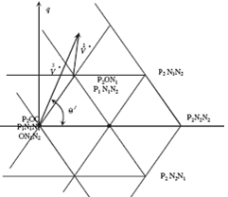
Рис. 5. Второй перенос вектора опорного напряжения
Определение времени задержки
После скорректированного опорного напряжения ![]() и определения соответствующего шестиугольника, мы можем применить обычный двухуровневый метод пространственно векторной ШИМ для расчета времени задержки; единственное различие между двухуровневой SVPWM и пятиуровневой SVPWM — в первых двух уравнениях появляется коэффициент 4, как показано в формулах (1–3). Оставшаяся процедура осуществляется как для обычного метода SVPWM для двухуровневого инвертора, и получаются два импульса одинакового уровня.
и определения соответствующего шестиугольника, мы можем применить обычный двухуровневый метод пространственно векторной ШИМ для расчета времени задержки; единственное различие между двухуровневой SVPWM и пятиуровневой SVPWM — в первых двух уравнениях появляется коэффициент 4, как показано в формулах (1–3). Оставшаяся процедура осуществляется как для обычного метода SVPWM для двухуровневого инвертора, и получаются два импульса одинакового уровня.
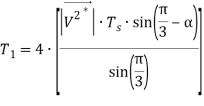 (1)
(1)
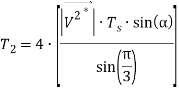 (2)
(2)
![]() (3)
(3)
Литература:
- Y. Liu, X. Wu, L. Huang, Implementation of three level inverter using a novel Space vector modulation 342 The European Physical Journal Applied Physics algorithm, Proc. IEEE Conf. on Power System Technology, Power Con 2002, 13–17 Oct. 2002, Vol.1, pp. 606–610.
- S. Wei, B. Wu, A General space vector PWM control algorithm for multilevel inverters, Eighteenth Annual IEEE on Applied Power Electronics Conference and Exposition, APEC’03, 9–13 Feb. 2003, Vol. 1, pp. 562–568
- G. S. Perantzakis, F. H. Xepapas, S. N. Manias, Efficient predictive current control technique for multilevel voltage source inverters, Proc. 11th EPE European Conference on Power Electronics and Applications, Dresden, 2005







