Не мыслям надобно учить, а мыслить.
И. Кант.
Современный ребёнок – это житель 21 века, на которого оказывают влияние все признаки настоящего времени. Он многим интересуется и о многом рассуждает, успевает освоить мобильный телефон и компьютер, телевизор и магнитофон. В то же время ребёнок по-прежнему сориентирован на самоценные, детские виды деятельности. Он любит играть, сочинять, фантазировать, радоваться и рассуждать.
Мои педагогические наблюдения позволили мне сделать вывод о том, что использование такого дидактического средства как логические блоки Дьенеша дает детям возможность верно улавливать причинно – следственные связи, находить параметры, связывающие различные на первый взгляд события и предметы, навык мыслить системно – это важнейшие условия успеха в профессиональной и личностной сфере, а значит развитие логического математического мышления – залог будущей успешности наших детей. Эта технология способствует развитию интеллекта, мыслительных операций, ведь подготовка к школе – это не только огромный запас знаний, который дает педагог, родитель, но и умение логически мыслить, анализировать, обобщать, классифицировать и самостоятельно приходить к нужным решениям.
Автор этой технологии Золтан Дьенеш – это венгерский профессор, создатель авторской методики обучения детей «Новая математика», согласно которой дети через игры осваивают сложные логические и математические концепции и системы. Использование данной технологии позволяет решить следующие задачи:
- Познакомить с формой, цветом, размером, толщиной объектов, понятием величины.
- Формировать представления о математических понятиях (алгоритм, кодирование и декодирование информации).
- Способствовать развитию у детей логического мышления, комбинаторики, аналитических способностей, формирует начальные навыки, необходимые детям в дальнейшем для умения решать логические задачи.
- Развивать представление о множестве, операции над множеством, пространственные представления.
- Развивать умения выявлять свойства в объектах, называть их, адекватно обозначать их отсутствие, обобщать объекты по их свойствам.
- Развивать познавательные процессы, мыслительные операции, творческие способности, воображение, фантазию, способности к моделированию и конструированию, развивать психические функции, связанные с речевой деятельностью.
- Воспитывать самостоятельность, инициативность, настойчивость в достижении цели, преодоление трудностей.
Что же представляет собой логические блоки Дьенеша? Это комплект из 48 геометрических фигур: четырех форм (круг, квадрат, треугольник, прямоугольник), трех цветов, двух размеров, двух видов толщины.
Комплект логических блоков дает возможность вести детей в их развитии от оперирования одним свойством предмета к оперированию двумя, тремя и четырьмя свойствами. В процессе разнообразных действий с блоками дети сначала осваивают умения выявлять и абстрагировать в предметах одно свойство, сравнивать, классифицировать и обобщать предметы по одному из этих свойств. Затем они овладевают умениями анализировать, сравнивать, классифицировать и обобщать предметы сразу по двум признакам, несколько позже – по трем и по четырем свойствам. При этом в одном и том же упражнении всегда можно варьировать правила выполнения задания с учетом возможностей детей. С логическими блоками ребенок выполняет различные действия: выкладывает, меняет местами, убирает, прячет, ищет, делит, а по ходу дела рассуждает.
Поскольку логические блоки представляют собой эталоны форм – геометрических форм, они могут использоваться при ознакомлении детей, начиная с раннего возраста, с формами предметов и геометрическими фигурами
Для проверки того, насколько хорошо дети освоили свойства геометрических фигур, вводится специальный код, графически изображающий данные свойства. Это позволяет развивать способность к моделированию и замещению свойств, умение кодировать и декодировать информацию. Эти способности и умения развиваются в процессе выполнения разнообразных предметно – игровых действий. Так, подбирая карточки, которые «рассказывают» о цвете, форме, размере и толщине блоков, дети упражняются в замещении и кодировании свойств, в процессе поиска блоков со свойствами, указанными на карточках, дети овладевают умением декодировать информацию и них, выкладывая карточки, которые «рассказывают» о всех свойствах блока, создают его своеобразную модель.
Карточки – свойства помогают детям перейти от наглядно – образного мышления к наглядно – схематическому, а карточки с отрицанием свойств – крохотный мостик к словесно – логическому мышлению. Логические блоки помогают ребенку овладеть мыслительными операциями и действиями, важными как в плане предматематической подготовки, так и с точки зрения общего интеллектуального развития. К таким действиям относятся: выявление свойств, их абстрагирование, сравнение, классификация, обобщение, кодирование и декодирование информации, а также логические операции «не», «и», «или». Более того, используя логические блоки, можно закладывать в сознание малышей начала элементарной алгоритмической культуры мышления, развивать у них способность действовать в уме, осваивать представления о числах и геометрических фигурах, пространственную ориентировку.
Целесообразно начать систематическую работу с использованием логических блоков со второй младшей группы. Прежде чем начать работу с детьми нужно установить, на какой ступеньке интеллектуальной лестницы находится каждый малыш. Сделать это несложно. Примерно ориентируясь на уровне развития ребенка предложить ему одну – две игры. Если он не справляется, предлагаем предыдущие по сложности игры. Самостоятельное и успешное решение задачи является той ступенькой, от которой начинается движение вперед. Проверив, таким образом, каждого ребенка, можно получить достаточно ясную картину уровня мыслительных умений детей. И это дает возможность организовать занятия с учетом уровня развития каждого ребенка. Если ребенок легко и безошибочно справляется с заданием определенной ступени – это сигнал к тому, что ему следует предложить игру следующей группы. Переводить ребенка к последующим играм можно только тогда, когда он «вырос» из предыдущих игр. Если же передержать детей на определенной ступени или преждевременно давать более сложные игры, то интерес к заданиям исчезает. Дети тянутся к мыслительным заданиям тогда, когда они для них трудноваты, но выполнимы.
Логические блоки Дьенеша можно использовать в различных видах деятельности:
- на занятиях, как комплексных, так и интегрированных, так как они хорошо обеспечивают наглядность, системность, смену деятельности;
- в аппликации, рисовании, помогают ориентироваться на плоскости;
- в конструировании, помогают ориентироваться в пространстве и закономерностях;
В методических пособиях предложено большое количество дидактических игр и каждую игру можно использовать в любой возрастной группе, тем самым предоставляется огромное поле деятельности для творчества педагога.
Дидактические игры с использованием логических блоков Дьенеша
|
Дидактическая игра |
Возрастная группа |
Задачи. |
Игровые действия |
|
1. «Бабочки»
|
2 младшая
|
Закреплять знания о геометрических фигуры, цветах. |
Дети работают на схеме, приемом наложения на схему. |
|
Средняя
|
Развивать логическое мышление, конструктивные способности. |
Дети работают по схеме, составляя изображение на горизонтальной поверхности. |
|
|
Старшая
|
Развивать умение раскодировать блоки с помощью знаков – символов, учить сравнивать и обобщать. |
Дети работают по схеме, разгадывая знаки – символы по 3 признакам.
|
|
|
Подготовительная
|
Развивать умение раскодировать блоки с помощью знаков – символов, включая знак отрицания некоторого свойства. |
Дети работают по схеме, разгадывая знаки – символы по 4 признакам, включая знак отрицания. |
|
|
2.«Разложи фрукты»
|
2 младшая
|
Закреплять знания о геометрических фигуры, цветах. |
Дети раскладывают «волшебные фрукты» (логические блоки) по обручам: раскладывают фигуры по цвету и форме; |
|
Средняя
|
Развивать логическое мышление, упражнять в классификации блоков по цвету и форме,
|
Дети находят область пересечения двух обручей и раскладывают фигуры по двум признакам (цвету и форме) |
|
|
Старшая
|
Учить выделять пересекающиеся подмножества, выделять общую часть множества, упражнять в классификации блоков по двум признакам, учитывая область пересечения. |
Дети находят область пересечения трёх обручей и раскладывают фигуры по трем признакам (цвету и форме, размеру), учитывая область пересечения
|
|
|
Подготовительная
|
Учить выделять пересекающиеся подмножества трех множеств, выделять их общие части, упражнять в классификации блоков по трем признакам, учитывая область пересечения |
Дети находят область пересечения трёх обручей и раскладывают фигуры по трем признакам (цвету и форме, размеру), учитывая область пересечения. |
|
|
3.«Дворец принцессы»
|
2 младшая
|
Закреплять геометрические фигуры, цвета. |
Злой волшебник заколдовал дворец принцессы и чтобы ей помочь надо схеме построить дворец: дети работают на схеме, приемом наложения на схему. |
|
Средняя
|
Развивать логическое мышление, конструктивные способности. |
дети работают по схеме, составляя дворец на горизонтальной поверхности; |
|
|
Старшая
|
Развивать умение раскодировать блоки с помощью знаков – символов по трем признакам, учить сравнивать и обобщать. |
дети работают по схеме, разгадывая знаки – символы по 3 признакам;
|
|
|
Подготовительная
|
Развивать умение раскодировать блоки с помощью знаков – символов по 4 признакам, включая знак отрицания некоторого свойства |
дети работают по схеме, разгадывая знаки – символы по 4 признакам, включая знак отрицания.
|
|
|
4.«Рассели жильцов»
|
2 младшая
|
Закреплять геометрические фигуры, цвета. |
Дети работают на схеме, приемом наложения на схему. |
|
Средняя
|
Развивать логическое мышление, упражнять в классификации.
|
Дети работают на схеме, выполняя словесное указание воспитателя (на первом этаже красные треугольники, на втором - синие квадраты, на третьем – желтые круги). |
|
|
Старшая
|
Упражнять в классификации и обобщении геометрических фигур по трем признакам. |
Дети работают по схеме, разгадывая знаки – символы по 3 признакам.
|
|
|
Подготовительная
|
Упражнять в счете. Развивать ориентировку в пространстве, внимание, логическое внимание. Упражнять в классификации и обобщении геометрических фигур по четырем признакам. |
Дети работают по схеме, разгадывая знаки – символы по 4 признакам, включая знак отрицания.
|
|
|
5.«Магазин»
|
2 младшая
|
Закреплять знания о геометрических фигурах, цветах. |
Дети, получая блок «деньги», ищут товар, на котором есть «ценник» с такой же фигурой по двум признакам. |
|
Средняя
|
Развивать логическое мышление, умение кодировать блоки с помощью знаков – символов по трем признакам. |
Дети, получая блок, ищут товар, на котором есть «ценник» с такой же фигурой (включается третий признак – размер). |
|
|
Старшая
|
Учить сравнивать и обобщать. Развивать логическое мышление, умение кодировать блоки с помощью знаков – символов, по четырем признакам. |
Дети, получая блок- «деньги», ищут товар, на котором есть «ценник» с его кодовым обозначением (включается четвертый признак – толщина). |
|
|
Подготовительная
|
Учить сравнивать и обобщать. Развивать логическое мышление, умение кодировать блоки с помощью знаков – символов включая знак «не». |
Дети, получая блок «деньги» ищут товар, на котором есть «ценник» с его кодовым обозначением со знаком «не» |
Логические блоки можно использовать при организации сюжетно-ролевых игр. Например, в игре «Магазин» деньги обозначаются блоками, цены на товар обозначаются кодовыми карточками; в игре «Почта» адрес на письме обозначается блоками, адрес на домике кодовыми карточками; в играх «Путешествие», «Цирк», «Театр» билеты обозначаются блоками, места кодовыми карточками.
Таким образом, анализируя результаты, можно сделать вывод: использование логических блоков Дьенеша в работе с детьми играет большую роль для развития их мышления и мыслительных операций.

Конспект НОД по познавательному развитию
«Путешествие в сказку «Снежная королева»
Задачи: Учить выделять пересекающиеся подмножества, выделять общую часть множества. Формировать умение работать с алгоритмами при выполнении практических действий, читать кодовое обозначение, раскодировать блоки, классифицировать геометрические фигуры по одному признаку, объединять блоки по двум признакам.
Развивать память, внимание, мышление, наблюдательность, свободное общение со взрослыми и сверстниками, все компоненты устной речи, расширять словарь, упражнять в подборе подходящих, близких по смыслу прилагательных, развивать пантомимические навыки детей.
Воспитывать доброжелательность, сплочённость детского коллектива, интерес к художественной литературе.
Материал: интерактивная доска, блоки Дьенеша на каждого ребёнка, два обруча: синий, красный; схемы: «Дворец», «Цветок» на каждого ребёнка; игрушка «сердце», две корзины, музыкальные проихведения.
Предварительная работа. Чтение сказки «Снежная королева».
Ход
Воспитатель. Ребята, я очень рада вас видеть, давайте посмотрим друг на друг и улыбнёмся, подарим радость друг другу.
Вы любите сказки? Я хочу пригласить вас совершить путешествие в сказку. Но в какую сказку вы узнаете, когда отгадаете загадку.
На санях, как ветер мчится,
К ней опасно прислониться
Лишь дотронься – заморозит,
В царство снежное увозит.
Злые чары в ход пускает –
Сердце в льдинку превращает.
Кто это? /Снежная королева/.
Воспитатель. Ребята, вы знаете сказку о Снежной королеве? /Ответы детей/. О чём рассказывается в этой сказке? /Ответы детей/. В сказке рассказывается о том, как осколок зеркала Снежной королевы попал в сердце Кая, и оно заледенело, мальчик стал злым. Снежная королева унесла его в свой дворец. А Герда отправилась на поиски своего друга, потому что очень любила его.
Воспитатель. В какое время года появилась Снежная королева? / Зимой /. Почему именно зимой, а не в другое время года? /Ответы детей/. А какое время года сейчас? /Зима/. Почему вы решили, что сейчас зима? /Ответы детей/. Потому метёт метель, холодно, снежно, морозно, день короткий, ночь длинная. А как вы думаете, Снежная Королева может сейчас за нами наблюдать. /Ответы детей/.
Воспитатель. Ребята, вы хотите помочь Герде найти Кая. /Ответы детей/. Давайте закроем глаза и представим, что мы вместе с Гердой отправились на поиски Кая. /Дети закрывают глаза/.
Воспитатель. Вот мы шли, шли и дошли до дворца, где живут Принц и Принцесса. И кого мы встретили у дворца? /Ответы детей/. Придворного ворона.
Придворный ворон сказал, что Принц и есть Кай и обещал представить Герду Принцу в том случае, если мы выполним задание с волшебными блоками. Слушайте задание: «Нужно расставить волшебные блоки по двум разноцветным обручам». Посмотрите на обручи и скажите, какого они цвета и как они расположены? /Ответы детей/. Обручи красного и синего цвета, расположены рядом друг с другом. Посмотрите на блоки, какие они? /Ответы детей/. Разные. А чем они отличаются? /Ответы детей/. По признаку цвета и по признаку формы.
Воспитатель. В красный обруч нужно положить красные блоки, в синий обруч - круглые. /Дети делятся на две подгруппы и выполняют задание/. По какому признаку объединены блоки в красном обруче, а в синем? /Ответы детей/. В красном обруче по признаку цвета, а в синем по признаку формы. Молодцы, ребята. А теперь соберем блоки в корзинки. /Дети собирают блоки в две корзины: в одну - красные блоки, в другую – круглые и садятся на стульчики/.
Воспитатель. Ребята, посмотрите на обручи и скажите, какой они формы. /Круглой/. Как вы думаете, можно ли из двух фигур одинаковой формы получить новую фигуру? /Ответы детей/. Я вам покажу, как из двух фигур круглой формы получить новую фигуру.
Воспитатель. Посмотрите на экран. Что вы видите? /Ответы детей/. Две окружности, которые расположены рядом друг с другом.
Я перемещаю один круг и располагаю его поверх другого. Что у нас получилось? /Ответы детей/. Два круга пересеклись («встретились»), и образовалась новая фигура.
Ребята, часть, где круги пересеклись, («встретились»), называется «область пересечения». Какая фигура образовалась в результате пересечения двух окружностей? /Овал/. Где расположен овал? /Посередине/.
Воспитатель. Ребята, я предлагаю вам взять обручи, показать на них область пересечения. /Дети выполняют задание/. Покажите, где расположена область пересечения. /Дети показывают область пересечения/. В области пересечения мы размещаем блоки, которые объединяют признаки тех блоков, которые расположены в красном и синем обруче.
Давайте вспомним, какие блоки мы располагали в красном и синем обруче, по какому признаку их объединяли. /Ответы детей/. В красный обруч располагали красные блоки, в синий обруч – круглые. В красном обруче объединены блоки по признаку цвета, а в синем по признаку формы. /Дети рассматривают блоки в корзинках, в одной - красные блоки, в другой – круглые/
Воспитатель. Как вы думаете, какие блоки мы можем разместить в области пересечения, если в красном обруче расположены красные блоки, а в синем обруче – круглые. /Ответы детей/. В области пересечения расположим блоки, объединённые по двум признакам: цвет и форма. Это – красные блоки круглой формы. / Дети выполняют задание/.
Молодцы, ребята, мы справились с заданием, которое нам задал Придворный ворон. Но Принц оказался не Каем. И Герда отправилась дальше.
Воспитатель. На своем трудном пути Герда попала к разбойникам. Какие были разбойники? /Злые/. Среди разбойников была девочка – дочка атаманши. Какой была дочка атаманши? /Ответы детей/. Она казалась злой, но на самом деле она была добрая. У девочки жили звери, и она за ними ухаживала. Какие звери жили у девочки? /Северный олень, лиса, зайцы/. Давайте изобразим зверей, которые жили у дочки атаманши.
Физкультминутка «Изобрази животное». Звучат музыкальные произведения, характеризующие животных. Дети идут по кругу и движениями, жестами, мимикой изображают важного северного оленя, хитрую лису и трусливых зайцев.
Воспитатель. Наконец-то мы с Гердой добрались до дворца Снежной королевы, но из-за сильной вьюги мы не можем его увидеть. У меня есть изображение дворца, но оно закодировано знаками, чтобы раскодировать его, нам нужно расшифровать все знаки. Вы знаете, как раскодировать знаки? /Дети объясняют, какими знаками закодирован дворец/.
Теперь мы знаем, из каких блоков состоит дворец Снежной королевы, и можем построить его. Предлагаю построить дворец из блоков по схеме. /Дети выполняют задание/.
/После того, как дети выполнили задание, на экране появляется изображение дворца Снежной королевы. Дети рассматривают дворец.
Воспитатель. Наконец Герда уставшая, изможденная добралась до дворца, каким она увидела дворец? /Ответы детей/. Холодный, мрачный, неприступный, злой. Мы нашли Кая, но он злой, у него холодный взгляд. Почему он такой злой? /Ответы детей/. Кай злой, потому что у него ледяное сердце.
Ребята, представьте, что у вас в руках льдинка. Что вы чувствуете? /Холод/. А как вы думаете, что нужно сделать, чтобы льдинка растаяла? /Ответы детей/. Нужно льдинку зажать в тёплых ладонях и она растает. Но у Кая не просто льдинка, а ледяное сердце. А как можно растопить ледяное сердце? /Ответы детей/. Тёплыми, ласковыми, нежными словами.
Ребят скажем Каю теплые, нежные, ласковые слова и его сердце растает. /Дети передают по кругу игрушку «сердце» и называют тёплые, ласковые, нежные слова/. Сердце Кая растаяло от ваших тёплых слов, и он стал добрым мальчиком. Кай и Герда обнялись друг с другом, давайте мы тоже обнимемся друг с другом. Они вернулись домой.
Воспитатель. Ребята, вам понравилось путешествие? Что понравилось больше всего? Что было сложным для вас? /Ответы детей/. Вместе мы справились со всеми трудностями. Молодцы! Я сейчас раздам вам схемы, на которых закодированы цветы. Когда вы раскодируете схемы, вы увидите, какие красивые цветы росли у Кая и Герды. До свиданья!
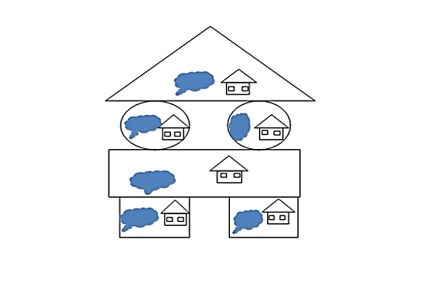
Схема «Дворец Снежной королевы»
Литература:
- Е. Н. Панова «Дидактические игры – занятия в ДОУ» Практическое пособие для воспитателей и методистов ДОУ. Воронеж: ЧП Лакоценин С. С., 2007.
- З. А. Михайлова, Е. А. Носова, А. А. Столяр, М. Н. Полякова «Теории и технологии математического развития детей дошкольного возраста» Изд. «Детство – Пресс», 2008.
- Е. В. Михеева «Новые подходы к организации логико-математического развития детей дошкольного возраста» журнал «Детский сад: теория и практика» № 1, 2012.
- М. Ю. Стожарова, Михалева С. Г. «Формы организации математической деятельности детей старшего дошкольного возраста» журнал «Детский сад: теория и практика» № 1, 2012.
- З. А. Михайлова, Е. А. Носова «Логико – математическое развитие дошкольников» Изд. «Детство – Пресс», 2013.
- Г. А. Репина «Математическое развитие дошкольников» современные направления. – М.: ТЦ Сфера, 2008.
- Е. А. Носова, Р. Л. Непомнящая «Логика и математика для дошкольников» методическое пособие. – СПб: «Акцидент», 1997.







