Идентификация критериального уравнения теплоотдачи экспериментальным данным при охлаждении алюминиевых слитков

 

В настоящее время изделия из алюминиевых сплавов находят всё большее применение. Одним из способов производства таких изделий является обработка давлением. Полуфабрикатами служат цилиндрические алюминиевые слитки, получаемые непрерывным литьём в охлаждаемый кристаллизатор. Как известно, при литье в водоохлаждаемый кристаллизатор ускоренное охлаждение слитков ведёт к появлению неравновесной структуры, ухудшающей качество слитка.

Для устранения дефектов слитка проводят термическую обработку, одним из видов которой является гомогенизационный отжиг. Важное влияние на структуру сплава оказывает скорость охлаждения после отжига. Охлаждение слитков после гомогенизации в промышленности реализуется несколькими способами, одним из которых является использование специальной камеры охлаждения.

Математическая модель теплообмена в камере охлаждения

Термическая обработка является одной из самых энергозатратных в тепловых технологиях. Задача снижения энергетических затрат является одной из приоритетных в современной энергетике. На величину энергетических затрат в процессе термической обработки оказывают влияние многие режимные и конструктивные факторы. Для оценки влияния данных факторов на конвективный теплообмен в камере охлаждения алюминиевых слитков авторами предложена математическая модель конвективного теплообмена в системе охлаждающий воздух — алюминиевые слитки [1]:

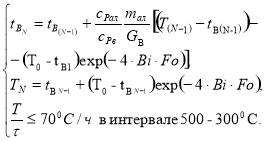
где  — температура охлаждающего воздуха при омывании слитка, ;  — температура охлаждающего воздуха при омывании предыдущего слитка, ;  — коэффициент теплоемкости алюминия, ;  — масса слитка, ;  — коэффициент теплоемкости воздуха, ;  — расход воздуха, ; T0 — начальная температура охлаждения слитка, ; ТN — температура слитка, ; Т(N-1) — температура предыдущегослитка, ; - критерий Био; - критерий Фурье; - скорость охлаждения слитка, .

В данной системе первое уравнение описывает изменение температуры охлаждающего воздуха, второе — изменение температуры слитка, третье — ограничение на максимальную скорость охлаждения слитков.

Решение данной математической модели предполагает определение коэффициента теплоотдачи . Движение воздуха происходит по каналам, ограниченным цилиндрическими слитками. Уравнения для расчета коэффициента теплоотдачи при турбулентном режиме движения при омывании волновой поверхности описана в работах [2, 3]. В работе Гомелаури В. И. [4] предложено критериальное уравнение теплоотдачи при омывании волновой поверхности:

(1)

где  — среднее значение критерия Нуссельта по длине канала;  — коэффициент теплопроводности, ;  — эквивалентный диаметр канала, ;  — среднее значение критерия Рейнольдса по длине канала;  — скорость охлаждающего воздуха, ;  — коэффициент кинематической вязкости, ;  — среднее значение критерия Прандтля по длине канала;  — среднее значение критерия Прандтля, определённое при температуре алюминиевых слитков;  — коэффициент, учитывающий увеличение теплоотдачи вследствие искусственной шероховатости

,

где  — шаг волн,  — расстояние между соседними волнами, ;  — высота волновой поверхности, .

Данное критериальное уравнение обобщает опытные данные по исследованию теплоотдачи внутри каналов круглого сечения, что является недостаточным для задачи конвективного теплообмена в системе «охлаждающий воздух — алюминиевые слитки», т. к. в этой системе поверхность теплообмена представляет собой канал, ограниченный горизонтальными рядами слитков. Поэтому для приведения данного уравнения к виду, где в качестве характерного размера используется высота канала , необходимо провести экспериментальные исследования.

Описание эксперимента:

Экспериментальное исследование теплообмена при охлаждении слитков проводилось на смонтированной камере охлаждения. Камера охлаждения представляет собой конструкцию, состоящую из рабочего пространства, в котором располагается садка; раздающего и собирающего газоходов. Для подачи охлаждающего воздуха на раздающем газоходе установлены четыре осевых вентилятора. При проведении эксперимента определялись зависимость температуры слитков в течение времени охлаждения, скорости охлаждающего воздуха. Температура слитков замерялась термопарами градуировки ХА, зачеканенными в слитки. Вторичным прибором служил измеритель — регулятор температуры 2ТРМ1. Скорость охлаждающего воздуха определялась путём пересчёта динамического давления, измеренного напорной трубкой. При проведении экспериментальных исследований погрешность измерений температуры слитков составляла , скорости охлаждающего воздуха .

Результаты экспериментальных значений температуры слитка представлены на рис. 1.

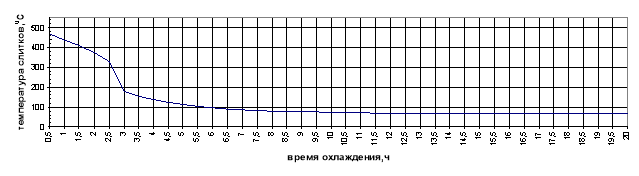
Рис. 1. Изменение температуры слитка в течение времени охлаждения

 

На графике показано изменение температуры слитка в одной точке измерения. Результаты экспериментальных значений скорости охлаждающего воздуха представлены на рис. 2.

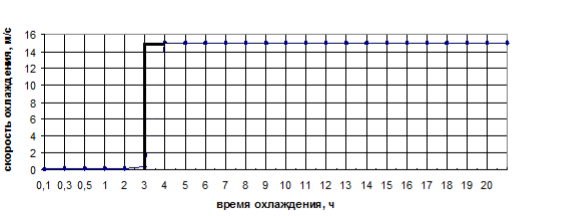
Рис. 2. Изменение скорости охлаждающего воздуха в течение времени охлаждения

 

Проведённое экспериментальное исследований теплообмена в камере охлаждения позволяет, используя полученные данные и метод наименьших квадратов, получить критериальное уравнение, где в качестве характерного размера используется высота канала .

Для аппроксимации экспериментальных данных степени соответствия между данными эксперимента и результатами определения коэффициента теплоотдачи по формуле (1) воспользуемся методом наименьших квадратов [5].

Экспериментальные данные аппроксимируем к уравнению, выражающему зависимость между критериями Нуссельта , Рейнольдса и Прандтля :

,

где  — постоянные числа. Для упрощения расчётов опустим значение критерия Прандтля , так как в интервале температур его значение почти не меняется.

Функция, подлежащая минимизации для определения оценок параметров методом наименьших квадратов, имеет вид [6]:

, (2)

где  — значение зависимой переменной в -ом эксперименте,  — значение независимой переменной,  — неизвестные коэффициенты, подлежащие определению.

Для определения неизвестных коэффициентов в (2) вычислим частные производные по и и приравняем их к нулю:

,

.

После проведения математических преобразований данных уравнений окончательно получим систему двух уравнений с двумя неизвестными:

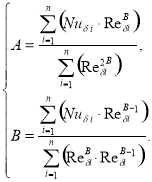(3)

Решая уравнение (3) методом подстановки, получим значения коэффициентов: и . Подставим данные коэффициенты в уравнение

.

С учётом критерия Прандтля окончательно получим

(4)

Выражение (4) представляет собой критериальное уравнение для определения коэффициента теплоотдачи в канале, ограниченном поверхностью алюминиевых слитков.

В результате экспериментального исследования были получены данные по характеру изменения температуры слитков и скорости охлаждающего воздуха. С использованием полученных данных проведена процедура идентификации критериального уравнения теплоотдачи. Это позволило получить критериальное уравнение, где в качестве характерного размера используется высота канала между горизонтальными рядами слитков. Данное уравнение можно использовать при инженерных расчётах.

 

Литература:

 

1. Горшенин, А.С., Кривошеев, В. Е. Исследование тепловых процессов при охлаждении алюминиевых слитков после их термической обработки / А. С. Горшенин, В. Е. Кривошеев // Энергетика и энергоэффективные технологии: Тр. V междунар.научно-практич. конф.- Липецк: 2012. — С. 60–62
2. Кружилин, Г. Н. Теория теплопередачи круглого цилиндра в поперечном потоке жидкости / Г. Н. Кружилин // ЖТФ, 1936. — т. 6, вып. 5. — с. 858–865.
3. Eckert, E. R. G. Die Berechnung des Warmeudergangen in der laminaren Grenzschicht umstromter Korper / E. R. G. Eckert // VDI — Forschungsh, 1942. — S. 1–26.
4. Гомелаури, В. И. Влияние искусственной шероховатости на конвективный теплообмен / В. И. Гомелаури // Труды института физики АН ГССР. — Тбилиси, 1963. — т. 9. — С. 111–145.
5. Горский, В.Г., Адлер, Ю.П., Талалай, А. М. Планирование промышленных экспериментов. — М.: Металлургия, 1978. — 279 с.
6. Соколов, А. К. Коэффициенты, упрощающие расчет теплопередачи через обмуровки печей. — Иваново: Ивановский государственный университет. 1980. — 11 с.