В статье рассматриваются некоторые задачи экономики, при решении которых используется нахождение площади плоской фигуры.
Ключевые слова: определенный интеграл, первообразная, кривая Лоренца, коэффициент Джини, добавочная выгода производителя и потребителя, математическая модель.
Данная статья принадлежит циклу статей с условным названием «Экономические приложения классических задач математического анализа» (см. [1], [2]) и является непосредственным продолжением темы «Приложения определенного интеграла к решению экономических задач», начатой в [2]. Здесь мы остановимся на использовании при решении экономических задач геометрического приложения определенного интеграла — вычисление площади плоской фигуры.
Вычисление добавочной выгоды (излишек) производителя и добавочной выгоды (излишек) потребителя
Потребительский излишек (добавочная выгода потребителя) ‒ это превышение общей стоимости, которую потребитель готов уплатить за все единицы товара, над его реальными расходами на их приобретение.
Рассмотрим кривую спроса ([4], с.33–34) некоторого товара, заданную как функцию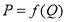 
, где 
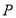‒ цена единицы товара, а 
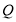‒ количество купленного товара. Очевидно, чем выше цена, тем меньше товаров будет куплено и наоборот.
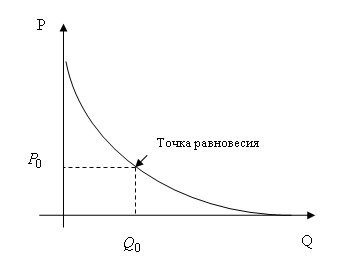
Рис. 1 Кривая спроса
Точка графика с координатами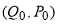 
(см. рис.1) соответствует ситуации, когда весь произведенный товар находит своего покупателя и все желающие могут купить данный товар. Такая точка называется точкой равновесия, при этом величина 
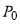‒ называется равновесная цена, а 
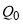- реализуемое по этой цене количество товара. Забегая вперед, отметим, что точка равновесия находится как точка пересечения кривой спроса и предложения, о которой речь пойдет ниже.
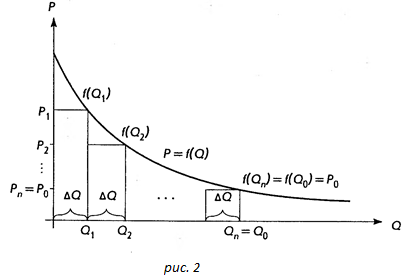
Предположим теперь, что товар в количестве 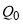не сразу весь попадает на рынок, а выбрасывается небольшими партиями равными 
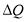. Это одна из распространенных тактик реализации товара. Цель продавца: поддержать цену на товар выше равновесной. Графически эта ситуация представлена на рис. 2.
Тогда общие затраты потребителей на все количество товара 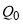согласно рис.2 будут следующими:
.
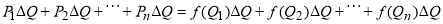Из рисунка 2 так же хорошо видно, что геометрически общие затраты потребителей равны сумме площадей прямоугольников, а она в свою очередь при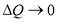 
стремится к площади криволинейной трапеции: 
.
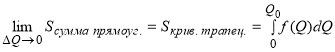Таким образом, суммарные затраты потребителей при продаже товара партиями 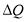, когда эти партии становятся сколько угодно малыми, будут равны: 
.
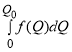По определению принимается, что излишек потребителя — это разность между предполагаемыми затратами потребителей и реальными затратами в условиях рынка, равными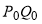 
. Если обозначить добавочную выгоду для потребителя через 
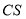, получим:
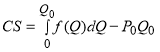. (1)
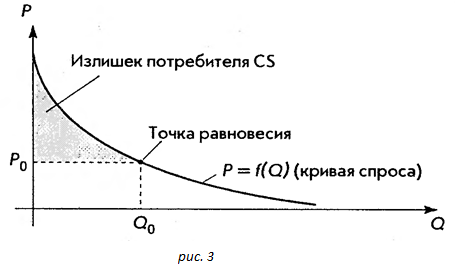
Графически 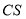‒ площадь фигуры, изображенной на рис.3.
Рассмотрим еще одно понятие рыночной экономики — добавочную выгоду, или излишек производителя. Излишек производства (добавочная выгода производства) ‒ разность между той денежной суммой, за которую он был готов продать товар и реальными доходами за реализованный товар. Для этого возьмем кривую предложения ([4], с. 44) некоторого товара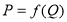 
.
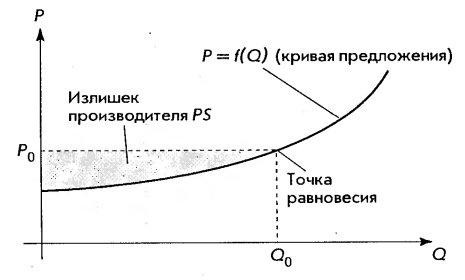
Рис. 4. Кривая предложения
Точно так же, как некоторые потребители, благодаря действию рыночных сил, получают возможность приобрести товар по цене ниже той, которую они были готовы заплатить, так и производители иногда получают возможность поставить товар на рынок по более высокой цене, чем ту на которую они были согласны. Действительно, кривая предложения дает различные цены, по которым производители готовы поставлять соответствующее количество товаров. Так, по цене 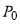будет поставлено количество товара 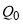. Предполагая, что весь товар 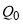будет реализован по цене 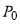, легко найти доход: 
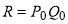. С другой стороны, количество товара, меньше чем 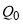, производители поставляли бы, согласно кривой предложения, по более низкой, чем 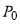, цене. Указанная на рисунке 4 закрашенная область, представляет добавочную выгоду производителя, обозначаемую 
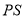. Площадь этой области, очевидно, вычисляется по формуле:
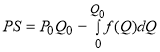. (2)
Задача № 1. Пусть кривая предложения имеет вид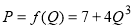 
, а точка равновесия достигается при количестве товара 
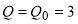. Требуется определить добавочную выгоду производителя .
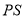Решение. Прежде из кривой предложения находим равновесную цену :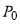 
.
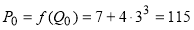Подставляя полученное значение в формулу (2) для добавочной выгоды производителя, получим:
.
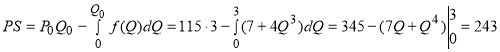Задача № 2. Известны законы спроса и предложения: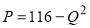 
, 
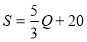. Найти выигрыш потребителей и выигрыш поставщиков, если было установлено рыночное равновесие.
Решение. Найдем точку рыночного равновесия из равенств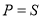а 
: 
. Откуда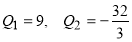 
. Так как по условию задачи 
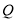‒ количество товара, то 
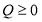. Следовательно, 
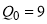. При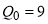 
равновесная цена составит 
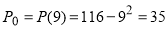, тогда доход на весь товар составит 
.
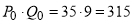Зная формулу выгоды потребителя (1) и формулу выгоды производителя (2), получим
; 
.
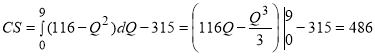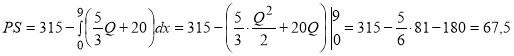Кривая Лоренца. Вычисление коэффициента Джини
Неравенство доходов в конце XIX — начале XX века стало объектом изучения многих экономистов США и Западной Европы. Центральной проблемой изучения является оценка справедливости и эффективности сложившегося в рыночной экономике распределения доходов и богатства. В 1905 году американский статистик Макс Лоренц разработал метод, названный его именем, оценки распределения доходов.
Кривая Лоренца([5], c.412)‒ это график, демонстрирующий степень неравенства в распределении дохода в обществе, отрасли, а также степени неравенства в распределении богатства. На оси абсцисс откладывается доля населения, а на оси ординат ‒ доля доходов в обществе в процентном отношении (см. рис.5).
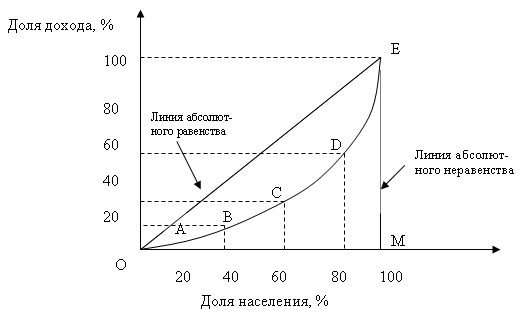
Рис. 5. Кривая Лоренца
Как видно из графика, в обществе всегда имеет место быть неравенство в распределении доходов, что отражает кривая OABCDE — кривая Лоренца. Например, первые 20 % населения могут получать 5 % доходов, 40 % населения — 15 % доходов, 60 % населения — 35 % доходов, 80 % населения — 60 % доходов, ну и естественно 100 % населения — 100 % доходов. Если бы в обществе было бы равное распределение дохода, то кривая Лоренца приняла бы вид прямой (биссектриса на графике), называемая линией абсолютного равенства, и, наконец, если бы в обществе весь доход получали только 1 % населения, то на графике это выразилось бы вертикальной прямой линией, называемойлинией абсолютного неравенства.
Кривая Лоренца позволяет судить о степени неравенства доходов в экономике по ее изгибу. Для количественного измерения степени неравенства дохода существует специальный коэффициент — коэффициент Джини, который равен отношению площади фигуры, ограниченной прямой абсолютного равенства и кривой Лоренца, к площади всего треугольника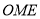 
:
.
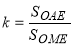Чем выше неравенство в распределении доходов, тем больше коэффициент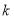 
приближается
к единице (абсолютное неравенство). И чем выше равенство в распределении доходов, тем меньше данный коэффициент. При абсолютном равенстве он достигает нуля.
Задача № 3. По данным исследования распределения доходов, в одной из стран кривая Лоренца, может быть описана уравнением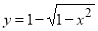 
, где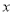 
- доля населения, 
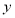— доля доходов населения. Найти коэффициент Джини.
Решение: Изобразим заданную кривую (см. рис.6).
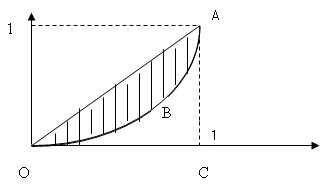
Рис. 6.
Это четверть окружности с центром в точке (0; 1), радиуса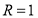 
, удовлетворяющая условиям 
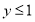(область изменения функции) и 
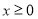(по смыслу задачи). Проведем также и биссектрису 
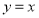. Тогда коэффициент Джини вычисляется по формуле: 
.
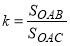Вычислим отдельно,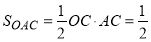 
;
.
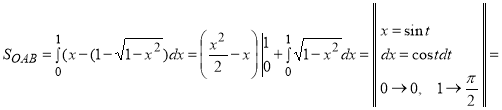
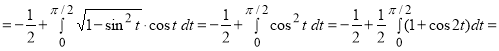
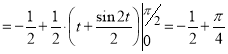Тогда коэффициент Джини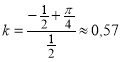 
.
Высокое значение коэффициента показывает существенное неравномерное распределение доходов среди населения в данной стране.
Литература:
- Ляликова Е. Р. Экономические приложения теории экстремумов функций двух переменных // Проблемы современной науки и образования. № 10(40), М., 2015. С.5–10.
- Ляликова Е. Р. Приложения определенного интеграла к решению задач экономики // Молодой ученый. № 19. 2015. с. 11–17.
- Красс М. С., Чупрынов Б. П. Основы математики и ее приложения в экономическом образовании. 4-е изд., испр. — М.: Дело, 2003. 688 с.
- Основы экономической теории. Курс лекций. Под редакцией Баскина А. С., Боткина О. И., Ишмановой М. С. Ижевск: Издательский дом «Удмуртский университет», 2000.
- Нуреев Р. М. Курс микроэкономики: Учебник для вузов.- 2-е изд., изм.-М.: Норма, 2005. 576 с.
- Солодовников А. С., Бабайцев В. А., Браилов А. В., Шандра И. Г. Математика в экономике: учебник: ч.2. М.: Финансы и статистика. 2007.- 560 с.
