В настоящей работе рассматривается обобщенная модель Фридрихса 
, действующих в прямом сумме 0 — и 1 — частичных подпространств Фоковского пространства.
Найден явный вид определителя возмущения. Обобщенная модель Фридрихса введена в работе [1], где были изучены ее собственные значения и «резонансы» (особенности аналитического продолжения резольвенты). Такие модели рассмотрены также в ряде других работ, из которых мы упомянем статью [2] — в ней результаты, полученные для обобщенной модели Фридрихса, применяются к проблемам случайного блуждания частицы в случайной среде, работу [3], в которой исследованы так называемые связанные состояния для определенного семейства обобщенных моделей Фридрихса, а также работу [4], где полностью исследован спектр модели и структура ее собственных векторов (как обычных, так и обобщенных) при малых значениях параметра взаимодействия. А в работе [5] оно рассматривается как двухканальная молекулярно-резонансная модель.
Пусть 
- трехмерный тор, т. е. куб 
— с соответствующим отождествлением противоположных граней. Всюду в работе рассматривается как абелева группа, в которой операции сложения и умножения на вещественное число введены как операции сложения и умножения на вещественное число в 
по модулю 
, где 
и 
- множество вещественных и целых чисел, соответственно. Например, если
,
то
.
Пусть 
— одномерное комплексное пространство и 
— гильбертово пространство квадратично-интегрируемых (комплекснозначных) функций, определенных на . Символом 
обозначается прямая сумма пространств 
и 
, т. е. 
. Пространства 
и 
называются нольчастичным и одночастичным подпространствами фоковского пространства 
по 
, соответственно, где
.
Элементы пространтсва 
представляются как векторы 
, где 
, 
. Для двух элементов ,
их скалярное произведение
в 
естественно определяется через скалярные произведения
.
Рассмотрим обобщенной модели Фридрихса 
, действующее в гильбертовом пространстве 
и задающихся как блочно–операторная матрица
,
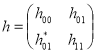где матричные элементы 
, 
, 
определяются равенствами
,
.
При этом 
— фиксированное вещественное число, 
и 
вещественнозначные непрерывные функции на 
, а 
сопряженное оператор к 
и
.
Здесь и в дальнейшем интеграл без указания пределов всюду означает интегрирование по всей области изменения переменных интегрирования.
Легко можно проверить, что оператор
, действующий в гильбертовом пространстве 
, является ограниченным и самосопряженным.
В математической физике оператор 
называется оператором уничтожения, а оператор 
называется оператором рождения. Оператор уничтожения снижает количество частиц в заданном состоянии на единицу, а оператор рождения увеличивает число частиц в данном состоянии на единицу, и является сопряженным к оператору уничтожения. Такие операторы имеют широкое применение в квантовой механике, в частности, в изучении квантовых гармонических осцилляторов и систем многих частиц [6].
Обозначим через 
, 
и 
, соответственно, спектр, существенный спектр и дискретный спектр ограниченного самосопряженного оператора.
Пусть оператор 
, действует в 
как
.
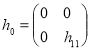Оператор возмущения 
оператора 
является самосопряженным оператором ранга 2. Следовательно, из известной теоремы Г. Вейля [7] о сохранении существенного спектра при возмущениях конечнего ранга вытекает, что существенный спектр оператора 
совпадает с существенным спектром оператора 
. Известно, что
,
где числа 
и 
определяются следующим образом:
.
Из последних фактов следует, что 
.
Определим регулярную в 
функцию (детерминант Фредгольма, ассоциированный с оператором 
)
.
Следующая лемма установит связь между собственными значениями оператора 
и нулями функции 
.
Лемма 1. Число 
является собственным значением оператора 
тогда и только тогда, когда 
.
Доказательство. Пусть число — есть собственное значение оператора 
и пусть 
— соответствующая собственная вектор-функция. Тогда эта вектор-функция удовлетворяет уравнению 
или системе уравнений
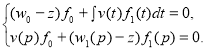(1)
Так как 
, из второго уравнения системы (1) для 
имеем
. (2)
Подставляя выражение (2) для 
в первое уравнение системы (1) заключаем, что система уравнений (1) имеет ненулевое решение тогда и только тогда, когда 
. Лемма 1 доказана.
Следующая теорема является основным результатом настоящей работы.
Теорема 1.Определитель возмущения 
оператора 
относительно оператора 
имеет вид
.
Доказательство. Так как
является оператором ранга 2, определитель возмущения хорошо определена по формуле (см. например [8])
,
где 
– единичный оператор в 
. Очевидно, что
.
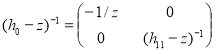Не нарушая общности предположим, что 
. Выбираем ортонормальный базис 
следующим образом:
и 
для любых 
.
Положим
.
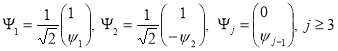По построению система 
является ортонормальной. Пусть
.
Здесь через 
обозначен множества натуральных чисел.
С помощью простых вычислений получим
;
;
;
;
в остальных случаях.
Здесь 
символ Кроникера. Следовательно,
.
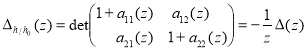Теорема 1 доказана.
Литература:
- С. Н. Лакаев. Некоторые спектральные свойства модели Фридрихса. Труды семинара им. И. Г. Петровского, 11 (1986), 210–223.
- К. Болдригини, Р. А. Минлос, А. Пеллегринотти. Случайные блуждания в случайной (флуктуирующей) среде. Успехи матем. наук, 62:4 (2007), 27–76.
- Е. Л. Лакштанов, Р. А. Минлос. Спектр двухчастичных связанных состояний трансфер-матриц гиббсовских полей (уединенное связанное состояние). Функц. анализ и его прил., 38:3 (2004), 52–69.
- Э. Р. Акчурин. О спектральных свойствах обобщенной модели Фридрихса. Теор. и матем. физика, 163:1 (2010), 17–33.
- A. K. Motovilov, W. Sandhas, Y. B. Belyaev. Perturbation of a lattice spectral band by a nearby resonance. J. Math. Phys., 42 (2001), 2490–2506.
- R. P. Feynman. Statistical mechanics: a set of lectures (2nd ed.). Reading, Massachusetts: Addison-Wesley, 1998, p. 151.
- М. Рид, Б. Саймон. Методысовременнойматематическойфизики. Т.4. Анализ операторов. М.: Мир, 1982.
- И. Ц. Гохберг, М. Г. Крейн. Введение в теорию линейных несамосопряженных операторов. М.: Наука, 1965.
