Блочно-операторная матрица — это матрица, элементы которой являются линейными операторами в банаховом или гильбертовом пространствах [1]. Одним из специальных классов блочно-операторных матриц являются Гамильтонианы системы с несохраняющимся числом квантовых частиц на целочисленной решетке. Их количество может быть неограниченным, как в случае моделей спин-бозонов [2,3] или ограниченным, как в случае урезанных моделей спин-бозонов [4,5]. Отметим, что такие системы обычно возникают в задачах физики твердого тела [6], квантовой теории поля [7], статистической физики [8], магнитогидродинамики [9] и квантовой механики [10].
В настоящей работе рассматривается блочно-операторная матрица 
(обобщенная модель Фридрихса), ассоциированная с системой не более, чем двух, квантовых частиц на 
–мерной решетке. Описывается его существенный и дискретный спектры. Найдены условия существования собственных значений.
Пусть 
– 
–мерный тор, т. е. куб 
— с соответствующим отождествлением противоположных граней. Всюду в работе 
рассматривается как абелева группа, в которой операции сложения и умножения на вещественное число введены как операции сложения и умножения на вещественное число в 
по модулю 
, где 
и 
- множество вещественных и целых чисел, соответственно. Например, если 
и
,
то
.
Пусть 
— одномерное комплексное пространство и 
— гильбертово пространство квадратично-интегрируемых (комплекснозначных) функций, определенных на 
. Символом 
обозначается прямая сумма пространств 
и 
, т. е. 
. Пространства 
и 
называются нольчастичным и одночастичным подпространствами фоковского пространства, соответственно.
Хорошо известно, что любой линейный ограниченный оператор 
, действующий в гильбертовом пространстве 
, всегда представляется как блочно-операторная матрица 
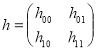,(1)
где матричные элементы
, 
являются линейными ограниченными операторами. Очевидно, что оператор 
тогда и только тогда, когда
.
В настоящей работе рассмотрим случай, когда операторы 
в формуле (1), определяются равенствами:
,
.
При этом 
— фиксированное вещественное число, 
и 
вещественнозначные непрерывные функции на 
, а 
сопряженное оператор к 
и
.
Полученный оператор обычно называется обобщенная модель Фридрихса и является ограниченным и самосопряженным.
Здесь и в дальнейшем интеграл без указания пределов всюду означает интегрирование по всей области изменения переменных интегрирования.
В математической физике оператор 
называется оператором уничтожения, а оператор 
называется оператором рождения.
Обозначим через 
, 
и 
, соответственно, спектр, существенный спектр и дискретный спектр ограниченного самосопряженного оператора.
Пусть оператор
, действует в 
как
.
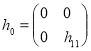Оператор возмущения 
оператора 
является самосопряженным оператором ранга 2. Следовательно, из известной теоремы Г. Вейля о сохранении существенного спектра при возмущениях конечного ранга вытекает, что существенный спектр оператора 
совпадает с существенным спектром оператора 
. Известно, что
,
где числа 
и 
определяются следующим образом:
.
Из последних фактов следует, что 
.
Определим регулярную в 
функцию (детерминант Фредгольма, ассоциированный с оператором 
)
.
Следующая лемма установит связь между собственными значениями оператора 
и нулями функции 
.
Лемма 1. Число 
является собственным значением оператора 
тогда и только тогда, когда 
.
Доказательство. Пусть число
— есть собственное значение оператора 
и пусть 
— соответствующая собственная вектор-функция. Тогда эта вектор-функция удовлетворяет уравнению 
или системе уравнений
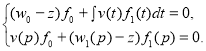(2)
Так как 
, из второго уравнения системы (1) для 
имеем
. (3)
Подставляя выражение (3) для 
в первое уравнение системы (2) заключаем, что система уравнений (2) имеет ненулевое решение тогда и только тогда, когда 
. Лемма 1 доказана.
Из леммы 1 вытекает, что
.
Таким образом
.
Так как функция 
является строго убывающей на полуосях 
и 
, то отсюда и из теоремы о предельном переходе под знаком интеграла Лебега следует, что существуют пределы (конечное или бесконечное)
;
.
По определению 
и 
.
Лемма 2.Оператор 
имеет единственное собственное значение, лежащее на 
, 
тогда и только тогда, когда 
.
Доказательство. Пусть 
, –собственное значение оператора 
. В силу леммы 1 это означает, что 
. Так как для любого 
имеет место соотношение
,
функция 
монотонно убывает на полуосях 
и 
. Следовательно, 
.
Обратно. Пусть для некоторого 
выполняется неравенство 
. Так как и функция монотонна и непрерывна в полуоси 
, то существует единственное число 
такое, что 
. По лемме 1 число 
– является собственным значением оператора 
. Лемма 2 доказана.
Следующая лемма доказывается аналогично.
Лемма 3.Оператор 
имеет единственное собственное значение, лежащее на 
, 
тогда и только тогда, когда 
.
Таким образом имеет место следующая теорема.
Теорема 1.
а) Если
, то оператор 
не имеет собственных значений на ;
б) Если 
, то оператор 
имеет единственное собственное значение на ;
в) Если 
, то оператор 
не имеет собственных значений на ;
г) Если 
, то оператор 
имеет единственное собственное значение на .
Доказательства теоремы 1 вытекает из леммы 2 и 3.
Следствие. Если 
и 
, то оператор 
имеет два собственных значений 
, причем 
и 
.
Литература:
- C. Tretter. Spectral Theory of Block Operator Matrices and Applications. Imperial College Press, 2008.
- H. Spohn. Ground states of the spin-boson Hamiltonian. Comm. Math. Phys., 123 (1989), 277–304.
- M. Huebner, H. Spohn. Spectral properties of the spin-boson Hamiltonian. Ann. Inst. Henri Poincare, 62:3 (1995), 289–323.
- Ю. В. Жуков, Р. А. Минлос. Спектр и рассеяние в модели «спин-бозон» с не более чем тремя фотонами. Теор. и матем. физика, 103:1 (1995), 63–81.
- R. A. Minlos, H. Spohn. The three-body problem in radioactive decay: the case of one atom and at most two photons. Topics in Statistical and Theoretical Physics, American Mathematical Society Translations–Series 2, 177 (1996), 159–193.
- A. I. Mogilner. Hamiltonians in solid state physics as multiparticle discrete Schroedinger operators: problems and results. AdvancesinSov. Math. 5 (1991), 139–194.
- К. О. Фридрихс. Возмущения спектра операторов в гильбертовом пространстве. М.: Мир, 1972.
- V. A. Malishev, R. A. Minlos. Linear infinite-particle operators. Translations of Mathematical Monographs. 143, AMS, Providence, RI, 1995.
- A. E. Lifschitz. Magnetohydrodynamic and spectral theory. Vol. 4 of Developments in Electromagnetic Theory and Applications. Kluwer Academic Publishers Group, Dordrecht, 1989.
- B. Thaller. The Dirac equation. Texts and Monographs in Physics. Springer, Berlin, 1992.
