Инволюция, уравнение Зильберштейна, обыкновенные дифференциальные уравнения с инволюцией, неоднородные дифференциальные уравнения с инволюцией.
In this paper is considered the problem to solve the second order no ordinary differential equation with involution.
Definition: If do reflected![]() , equality
, equality![]() . This reflect is involution.
. This reflect is involution.
Such functions ![]() arrange an involution.
arrange an involution.
The properties of involution is take possession a lot of problem full give at the [1] article.
Following
![]() (1)
(1)
Looking the equation.
Theorem: If be ![]() that is involution
that is involution ![]() at the equation (1), then equation (1) limit step after the problem be solved is form second order the equation differential.
at the equation (1), then equation (1) limit step after the problem be solved is form second order the equation differential.
Prove: The equality (1) for be solved, this the is equality the aspect writing
![]()
its differentiated, as a result is form equality
![]()
![]() (2)
(2)
Looking the involution is take notice at the equality (1), exchange the ![]() this
this![]() ,
,
following form equality
![]() (3)
(3)
in accordance the equality (3) and (2)
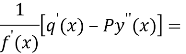
The second order, vulgar differential equation integration problem is form
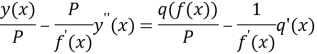 (4)
(4)
exchanged elementary as a result is property of the involution that equation (1) is solution of problem at the this equation. ![]()
Example:
![]()
Accordance (4) equality solution
![]() (5)
(5)
Mean
![]()
![]()
![]()
-
If be (1) equality being
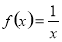
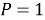
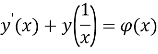 (6)
(6)
(4) equality as being
![]() (7)
(7)
![]() or
or
![]()
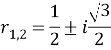
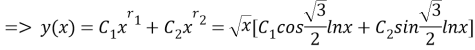
Also,
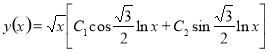 (8)
(8)
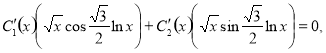
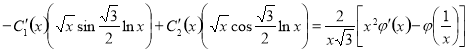
Thisequality
![]()
![]()
![]() ,
,
![]()
![]()
![]()
Reference:
- Винер И. Я. Дифференциальные уравнения с инволюциями. // Дифференциальные уравнения. Том 5, 1969.
- Хромов А. П. Смешанная задача для дифференциального уравнения с инволюцией и потенциалом специального вида. // Известия Саратовского Университета, Нов.сер. Математика, Механика, Информатика. 2010,,т.10. вып № 4,с.17–22.
- Курдюмов В. П., Хромов А. П. О базисах Рисса из собственных и присоединенных функций функционально-дифференциального оператора переменной структуры. //Изв. Сарат.унта. Нов.сер.Математика. Механика. Информатика.2007.Т.7, вып.2, С. 20–25.







