Обобщенная модель Фридрихса и ее собственное пороговое значение

 

В настоящей работе рассматривается обобщенная модель Фридрихса , действующих в прямом сумме 0 — и 1 — частичных подпространств фоковского пространства.

Обсуждается случай, когда параметр функция этого оператора имеет специальный вид. Показывается, что эта функция имеет невырожденный минимум в нескольких различных точках трехмерного тора . Найдены необходимые и достаточные условия для того, чтобы, число являлось собственным значением оператора , в зависимости от точки минимума функции . При этом нуль является нижней гранью существенного спектра оператора .

Пусть - трехмерный тор, т. е. куб  — с соответствующим отождествлением противоположных граней,  — одномерное комплексное пространство и  — гильбертово пространство квадратично-интегрируемых (комплекснозначных) функций, определенных на . Символом обозначается прямая сумма пространств и , т. е. . Пространства и называются нольчастичным и одночастичным подпространствами фоковского пространства, соответственно.

Рассмотрим обобщенной модели Фридрихса , действующее в гильбертовом пространстве и задающихся как блочно–операторная матрица

,

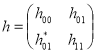где матричные элементы , , определяются равенствами

,

.

При этом  — фиксированное вещественное число, -вещественнозначная четная дважды непрерывно дифференцируемая функция на , а функция определена по формуле

.

А оператор сопряженное оператор к и .

Здесь и в дальнейшем интеграл без указания пределов всюду означает интегрирование по всей области изменения переменных интегрирования.

Легко можно проверить, что оператор , действующий в гильбертовом пространстве , является ограниченным и самосопряженным.

Пороговые явления для двухчастичного дискретного оператора Шредингера изучены в работах [1–3], a для семейства модели Фридрихса с одномерным возмущением, которые ассоциированы с системой двух частиц на решетке изучены в работах [4,5]. Как известно, некоторые актуальные задачи, в частности, задачи квантовой механики, статистической механики и гидродинамики сводятся к исследованию спектральных свойств обобщенной модели Фридрихса [6–8]. Поэтому изучение пороговое собственное значение для обобщенной модели Фридрихса играет важную роль в современной математической физике.

Обозначим через , и , соответственно, спектр, существенный спектр и дискретный спектр ограниченного самосопряженного оператора.

Пусть оператор , действует в как

.

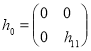Оператор возмущения оператора является самосопряженным оператором ранга 2. Следовательно, из известной теоремы Г. Вейля [9] о сохранении существенного спектра при возмущениях конечнего ранга вытекает, что существенный спектр оператора совпадает с существенным спектром оператора . Известно, что .

Из последних фактов следует, что .

Определим регулярную в функцию (детерминант Фредгольма, ассоциированный с оператором )

.

Рассмотрим точки из , для которых ,

причем при . Ясно, что число таких точек равно 27.

Легко проверяется, что функция имеет невырожденный минимум в точках , . Функция является непрерывной на , поэтому существует конечный интеграл

.

Из теоремы о предельном переходе под знаком интеграла Лебега следует, что .

Следующая теорема о необходимых и достаточных условиях для того чтобы, число являлось собственным значением оператора .

Теорема 1. Оператор имеет нулевое собственное значение тогда и только тогда, когда и .

Доказательство.Необходимость. Пусть оператор имеет нулевое собственное значение и  — соответствующая собственная вектор–функция. Тогда и удовлетворяют уравнению или системе уравнений

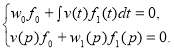(1)

Из второго уравнения системы (1) для имеем

. (2)

Подставляя выражение (2) для в первое уравнение системы (1) заключаем, что . Теперь докажем, что тогда и только тогда, когда , . Действительно, если при некотором верно , то из четности дважды непрерывна дифференцируемой функции следует, что существуют числа и , такие, что

, (3)

где .

Кроме того из определения функции для некоторых и получим, что

, (4)

.(5)

Имеет место равенство

. (6)

Учитывая неравенства (3)-(5) имеем, что –ая () слагаемая в правой части (6) конечна тогда и только тогда, когда . В случае , имеем

.

Таким образом тогда и только тогда, когда , .

Достаточность. Пусть и . Тогда легко можно проверить, что вектор–функция , где , а определен по формуле (2), удовлетворяет уравнению . Выше доказали, что если , то . Теоремы 1 доказано.

В ходе доказательства теоремы 1 показали, что если оператор имеет нулевое собственное значение, вектор–функция , где , а определен по формуле (2), удовлетворяет уравнению и .

Отметим, что теорема 1 играет важную роль при изучении конечности или бесконечности дискретного спектра соответствующего трехчастичного модельного оператора в зависимости от точки минимума функции .

 

Литература:

 

1.      Albeverio S., Lakaev S. N., Makarov K. A., Muminov Z. I. The threshold effects for the two-particle Hamiltonians in lattice. Comm. Math. Phys. 262 (2006), P. 91–115.
2.      Albeverio S., Lakaev S. N., Muminov Z. I. Schroedinger operators on lattices. The Efimov effect and discrete spectrum asymptotics. Ann. Henri Poincare. 5 (2004), P. 743–772.
3.      Абдуллаев Ж. И., Лакаев С. Н. Асимптотика дискретного спектра разностного трехчастичного оператора Шредингера на решетке. Теор. и мат. физ., 136:2 (2003), С. 231–245.
4.      Albeverio S., Lakaev S. N., Muminov Z. I. The threshold effects for a family of Friedrichs models under rank one perturbation. J. Math. Anal. Appl. 330 (2007), P. 1152–1168.
5.      Albeverio S., Lakaev S. N., Djumanova R. Kh. The Essential and Discrete Spectrum of a Model Operator Associated to a System of Three Identical Quantum Particles. Rep. Math. Phys. 63:3 (2009), P. 359–380.
6.      Фаддеев Л. Д. О модели Фридрихса в теории возмущений непрерывного спектра. Труды Мат. Инс-та АН СССР, 73 (1964), С. 292–313.
7.      Минлос Р. А., Синай Я. Г. Исследование спектров стохастических операторов, возникающих в решетчатых моделях газа. Теор. и матем. физ. 2:2 (1979), С. 230–243.
8.      Дынкин Е. М., Набако С. Н., Яковлев С. И. Граница конечности сингулярного спектра в самосопряженной модели Фридрихса. Алгебра и анализ. 3:2 (1991), С. 77–90.
9.      Рид М., Саймон Б. Методы современной математической физики. Т. 4, Анализ операторов. — М., Мир, 1982.