В настоящее время матричное исчисление широко применяется в различных областях математики, механики, теоретической физики, теоретической электротехники и т. д.
Пусть ![]() — матрицы
— матрицы ![]() с комплексными элементами. В данной работе дадим 5 разные доказательство следующего утверждения.
с комплексными элементами. В данной работе дадим 5 разные доказательство следующего утверждения.
Теорема 1.Матрицы ![]() и
и ![]() имеют одинаковые собственные значение.
имеют одинаковые собственные значение.
Сначала приводим некоторые общеизвестные факты [1–4].
Пусть ![]() – след матрицы
– след матрицы ![]() , а
, а ![]() детерминант матрицы
детерминант матрицы ![]() . Тогда имеют место следующие соотношение:
. Тогда имеют место следующие соотношение:
![]() ;(1)
;(1)
![]() ;(2)
;(2)
и они хорошо известны в курсе линейной алгебры.
Под следом матрицы ![]() понимают сумму диагональных элементов этой матрицы:
понимают сумму диагональных элементов этой матрицы:
Нетрудно видеть, что
![]() ,
,
если ![]() – характеристические числа матрицы
– характеристические числа матрицы ![]() .
.
Доказательство равенство (1) очевидно. Докажем соотношение (2).
Пуст
![]()
характеристический многочлен матрицы ![]() ,
, ![]() –его корни с учетом кратности. Они являются характеристическими числами матрицы
–его корни с учетом кратности. Они являются характеристическими числами матрицы ![]() . Известно, что
. Известно, что ![]() является
является ![]() –ый элементарный многочлен этих чисел. Следовательно,
–ый элементарный многочлен этих чисел. Следовательно,
![]() ;
;
![]() ;
;
![]()
Чтобы доказать теоремы 1 надо показать, что
![]() (3)
(3)
для всех ![]() .
.
Мы знаем, что этот факт верны в случаях ![]() и
и ![]() . Докажем, что оно верна при остальных значениях
. Докажем, что оно верна при остальных значениях ![]() .
.
Доказательство 1. Достаточно показать равенство
![]() (4)
(4)
при всех ![]() . Подчеркнем, что характеристические числа матрицы
. Подчеркнем, что характеристические числа матрицы ![]() является
является ![]() –ый степень характеристических чисел матрицы
–ый степень характеристических чисел матрицы ![]() . Таким образом,
. Таким образом,
![]() .
.
Поэтому соотношение (4) эквивалентно следующему
![]() .
.
С другой стороны из (1) вытекает, что
![]() .
.
Это и завершает доказательство теоремы 1.
Доказательство 2. Соотношение (3) можно доказать непосредственно. Коэффициент ![]() является суммой всех принципиальных миноров порядка
является суммой всех принципиальных миноров порядка ![]() матрицы
матрицы ![]() . Прямые вычисления (с помощью формулы Бине–Коши) приводят соотношению (3). Более софистская версия этого аргумента включается анти–симметрической тензорной произведений
. Прямые вычисления (с помощью формулы Бине–Коши) приводят соотношению (3). Более софистская версия этого аргумента включается анти–симметрической тензорной произведений ![]() . Оно является матрицей порядка
. Оно является матрицей порядка ![]() , элементы который будут миноры порядка
, элементы который будут миноры порядка ![]() матрицы
матрицы ![]() . Тогда
. Тогда
![]() .
.
Один из важных свойств ![]() является следующая:
является следующая:
![]() .
.
Следовательно,
![]() .
.
Это и завершает доказательство теоремы 1.
Доказательство 3. Это доказательство вводит аргумент непрерывности, который полезный во многих контекстах. Предположим, что ![]() обратимая (не сингулярная) матрица. Тогда
обратимая (не сингулярная) матрица. Тогда
Поэтому ![]() и
и ![]() являются подобными, и следовательно, имеют одинаковые собственные значение. Таким образом, соотношение (3) верно в случае, когда
являются подобными, и следовательно, имеют одинаковые собственные значение. Таким образом, соотношение (3) верно в случае, когда ![]() обратимо. Чтобы доказать в общем случае мы нуждаемся два факта: а) Если
обратимо. Чтобы доказать в общем случае мы нуждаемся два факта: а) Если ![]() не сингулярная, мы можем выбрать последовательность не сингулярных матриц
не сингулярная, мы можем выбрать последовательность не сингулярных матриц ![]() такое, что
такое, что ![]() . б) Функция
. б) Функция ![]() есть многочлен элементов матрицы
есть многочлен элементов матрицы ![]() , и следовательно, они непрерывны. Таким образом, если
, и следовательно, они непрерывны. Таким образом, если ![]() сингулярная, то мы можем выбрать последовательность не сингулярных матриц
сингулярная, то мы можем выбрать последовательность не сингулярных матриц ![]() такое, что
такое, что ![]() и заметим, что
и заметим, что
![]() .
.
Это и завершает доказательство теоремы 1.
Доказательство 4. В этом доказательстве используется блочные матрицы ![]() . Рассмотрим матрицы
. Рассмотрим матрицы ![]() вида
вида
![]() ,
,
элементы, которых являются матрицы ![]() , а
, а ![]() есть нулевая матрица. Характеристические число этой матрицы есть
есть нулевая матрица. Характеристические число этой матрицы есть ![]() характеристические числа матриц
характеристические числа матриц ![]() и
и ![]() . Детерминант этой матрицы равно
. Детерминант этой матрицы равно
![]() .
.
Для любой матрицы ![]() порядка
порядка ![]() , матрица
, матрица
![]()
порядка ![]() является обратимым, и его обратное имеет вид
является обратимым, и его обратное имеет вид
Учитывая этот факт получим, что
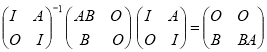 .
.
Следовательно, матрицы
![]()
и
![]()
подобны, и поэтому имеют одинаковые характеристические числа. Таким образом, матрицы ![]() и
и ![]() имеют одинаковые характеристические числа. Это и завершает доказательство теоремы 1.
имеют одинаковые характеристические числа. Это и завершает доказательство теоремы 1.
Доказательство 5. Пусть ![]() идемпотентная матрица, т. е.
идемпотентная матрица, т. е. ![]() . Тогда
. Тогда ![]() является оператором проектирования (не обязательно ортогональной). В этом случае, некотором базисе (не обязательно ортонормальной) матрица
является оператором проектирования (не обязательно ортогональной). В этом случае, некотором базисе (не обязательно ортонормальной) матрица ![]() записывается как
записывается как
![]() .
.
В этом базисе пусть
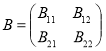 .
.
Тогда
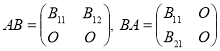 .
.
Поэтому ![]() и
и ![]() имеют одинаковые собственные числа. Пусть теперь
имеют одинаковые собственные числа. Пусть теперь ![]() произвольная матрица. Тогда существует обратимая матрица
произвольная матрица. Тогда существует обратимая матрица ![]() такое, что
такое, что
![]() .
.
Заметим, что ![]() есть идемпотентная матрица и применяем специальный случай подставляя вместо
есть идемпотентная матрица и применяем специальный случай подставляя вместо ![]() матрицы
матрицы ![]() , а вместо
, а вместо ![]() матрицы
матрицы ![]() . Это показывает, что
. Это показывает, что ![]() и
и ![]() имеют одинаковые характеристические числа. С другими словами,
имеют одинаковые характеристические числа. С другими словами, ![]() и
и ![]() имеют одинаковые характеристические числа. Это и завершает доказательство теоремы 1.
имеют одинаковые характеристические числа. Это и завершает доказательство теоремы 1.
Пусть ![]() и
и ![]() две линейные ограниченные операторы в гильбертовом пространстве
две линейные ограниченные операторы в гильбертовом пространстве ![]() . Тогда ненулевые элементы спектров операторов
. Тогда ненулевые элементы спектров операторов ![]() и
и ![]() совпадают.
совпадают.
Пусть ![]() и
и ![]() две прямоугольные матрицы. Если обе произведение
две прямоугольные матрицы. Если обе произведение ![]() и
и ![]() имеют смысл, то ненулевые характеристические числа
имеют смысл, то ненулевые характеристические числа ![]() и
и ![]() совпадают.
совпадают.
Литература:
- Ф. Р. Ганхмахер. Теория матриц. — 4-е изд. –М.: Наука, 1988.
- R. Bhatia. Matrix analysis. Springer-Verlag, New York, 1997.
- R. Bhatia. Positive definite matrices. In: Princeton Series in Applied Mathematics. Princeton University Press, 1997
- F. Nielsen, R. Bhatia. Matrix Information Geometry. Springer, XII, 2013, 454.







