Эйлеровы методы моделирования потоков со свободной поверхностью

Ключевые слова: эйлеровы методы, лагранжевы методы, численные методы, расчетная сетка, свободная поверхность, VOF, МАС, алгоритм реконструкции.

В работе представлен анализ и классификация существующих методов расчета потоков со свободной поверхностью, основанных на подходе Эйлера к описанию потоков движущихся жидкостей. Течения со свободной поверхностью играют важную роль во многих сферах науки и техники. Определение положения поверхности раздела сред необходимо при решении задач технической гидравлики. Вычисление точного положения поверхностей раздела фаз при решении сложных задач, в настоящее время, возможно только при создании сложных математических моделей, основанных на численных методах, или путем проведения лабораторных экспериментов.

Свободная поверхность потока — граница между жидкостью и находящимся над ней газом. В большинстве из решаемых задач инженерной гидравлики, плотность жидкости во много раз больше плотности газа, что позволяет пренебрегать влиянием воздуха на движущуюся жидкость.

Для решении многих задач гидротехники, мелиорации и водоснабжения необходимо определять форму и положение границы раздела потока движущейся жидкости. Характерными случаями такого типа являются такие нестационарные задачи как: набеганние морских волн на препятствие, обрушение резервуаров, плотин, подпорных стен. В качестве стационарных задач могут рассматриваться: истечение жидкости через затворы плотин водохранилищ, обтекание водосливов и вертикальных опор мостов, движение жидкостей в мелиоративных каналах.

Существует большое количество методов расчета потоков, в которых используются различные способы определения положения свободной поверхности потока жидкости. По способу преобразования уравнений движения среды, различные численные алгоритмы решения гидравлических задач о движении жидкостей с открытой поверхностью можно разделить на 2 вида: на лагранжевы и эйлеровы.

В методах, основанных на подходе Лагранжа, положение свободной поверхности определяется либо узлами подвижной расчетной сетки, либо частицами, переносящими материальные и динамические свойства среды. В методах, основанных на подходе Эйлера, для определения положения свободной поверхности вводятся различные маркеры, которые движутся вместе со средой и не влияют на ее динамику. Роль маркеров могут выполнять точечные частицы, помещаемые вдоль свободной поверхности или в весь объем жидкости, так и пространственные маркер-функции [1].

Эйлеровы методы основаны на подходе Эйлера к записи уравнений движения потока. Эйлеров подход в описании движения заключается в определении характеристик потока сплошной среды в выбранной геометрической точке рассматриваемого пространства. Таким образом в пространстве выбирают точку А, координаты которой имеют значения x, y, z. Движение потока в фиксированном месте, с точки зрения Эйлера, считается известным, если известны функции [2]:

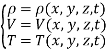(1)

Уравнение массы при использовании подхода Эйлера имеет вид [3]:

(2)

Уравнение импульса в подходе Эйлера примет вид [3]:

(3)

Исходя из сравнения подходов Эйлера и Лагранжа [4] можно сделать вывод, что с точки зрения Лагранжа, рассматриваются законы изменения гидродинамических характеристик для выбранной точки сплошной среды, а с точки зрения Эйлера — законы изменения характеристик в выбранном месте потока жидкости.

В эйлеровых алгоритмах для дискретизации уравнений движения среды используется, как правило, неподвижная расчетная сетка (в ряде случаев сетка может быть деформируемой в определенных пределах, например, для учета перемещения твердых границ). При этом межфазная граница перемещается по сетке, и для определения ее положения нужны специальные методики. В качестве основных методик используют методы MAC, VOF и метод поверхностных маркеров.

Метод MAC относится к классу методов, расчеты которого проводятся на неподвижной сетке. Для определения наполненности жидкостью ячеек расчетной области используются точечные частицы-маркеры, распределённые по объему жидкости и движущиеся вместе с ней. Вводимые в поток частицы-маркеры не занимают объема и не влияют на характер течения. В этом методе ячейка сетки будет содержать жидкость, если имеет внутри себя хотя бы один маркер, если нет, то ячейка пуста.

Достоинством такого метода является возможность расчета сложных течений с объединением и разделением объемов жидкости. Это достоинство обусловлено тем, что маркеры отслеживают движение единичных объемов жидкости, а не точек положения свободной поверхности. Таким образом свободная поверхность определена как граница объема, занятого жидкостью, посредством этого, поверхности потоков могут свободно объединяться и распадаться.

Недостатками MAC являются: низкая экономичность (расчет достаточно большого количества маркеров), при недостатке частиц снижется точность и появляется возможность образования нефизичных пустот в потоке.

Практическое применение метода МАС ограничивалось преимущественно двумерными задачами; на сегодняшний день данный метод почти не используется [1]. Методы, использующие функцию маркер, имеют возможность моделировать наиболее сложные течения. Схема определения свободной поверхности представлена на рис. 1.

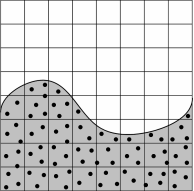
Рис. 1. Определение положения свободной поверхности по положению дискретных маркеров при использовании метода МАС [1]

Суть метода поверхностных маркеров заключается в том, что точечные частицы-маркеры расположены не в объеме жидкости, а только на поверхности раздела. Данный метод является более экономичным по сравнению с методом MAC, а также позволяет более точно описывать контактную границу и поверхностное натяжение. Недостатком же является то, что в данном методе при поверхностном распределении маркеров расчет течений со слиянием или разделением объемов жидкости становится проблематичным. Также сохранена проблема потери точности расчетов, за счет уменьшения концентрации маркеров при сильной деформации свободных поверхностей, присутствовшая и в методе MAC. Метод поверхностных маркеров является наиболее эффективным при решении двумерных задач, однако данная методика с трудом обобщается на трехмерный случай. В связи с этим практическое применение метода поверхностных маркеров не вышло за рамки двумерных задач [1]. Схема определения свободной поверхности представлена на рис. 2.

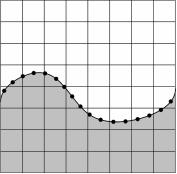
Рис. 2. Определение положения свободной поверхности по положению дискретных маркеров при использовании метода поверхностных маркеров [1]

Метод VOF (Volume-of-Fluidmethod) является в настоящее время наиболее популярным и используется в известных программах вычислительной гидродинамики, таких как ANSYS Fluent, Star-CD и CFX, Flow-3D.

В методе вместо функции маркера используют специальную функцию объемной доли жидкости в ячейке расчетной сетки — С. Если в элементе сетки доля жидкости С=1 — ячейка заполнена жидкостью, если С=0 — то ячейка пуста. Границе раздела сред соответствует значение величины 0<С<1. В отличие от MAC, в методе VOF необходимо хранить в ячейке только одну переменную, что делает метод намного более экономичным в отношении вычислительной мощности.

Важной частью метода является алгоритм реконструкции свободной поверхности на основе значений С. Существует несколько основных подходов [5]:

1.                SLIC — Simple Line Interface Calculation. В SLIC методе граница раздела фаз представлена вертикальной или горизонтальной линией и определяется из величины функции С в соседних ячейках;
2.                b) P&Y — Parker and Young’s method. В данном методе свободная поверхность жидкости в ячейке представляется в виде прямой, угол наклона 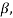которой определятся из выражения ;
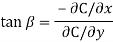3.                Least squares volume-of-fluid reconstruction algorithm (LVIRA).Свободная поверхность жидкости в ячейке представляется в виде наклонной прямой,угол наклона которой определяется из условия минимизации функции:

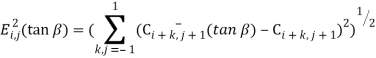(4)

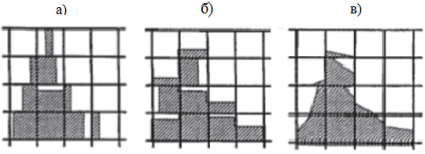
Рис. 3. Схематическое представление результатов реконструкции свободной поверхности в методе VOF: а, б — алгоритм SLIC, в — алгоритм P&Y[5]

На основе представленных данных о методах расчета потоков со свободной поверхностью основанных на Эйлеровом подходе к изучению движения жидкости можно сделать следующие выводы:

1.                Эйлеровы методы являются наиболее эффективными в практическом плане, за счет возможности пользовательского изменения структуры и размеров расчетной сетки в зависимости от рассматриваемой задачи;
2.                Метод MAC, основанный на добавлении маркеров в поток жидкости, является пригодным для решения сложных задач, но является наиболее ресурсозатратным;
3.                Метод поверхностных маркеров не пригоден для решения сложных задач, но является менее требовательным к вычислительной мощности;
4.                Наиболее распространённым и доступным является метод VOF, основанный на нахождении объёмной доли жидкости в ячейках. Данный метод является оптимальным по спектру решаемых задач и экономии ресурсов, требуемых для решения задачи.

Литература:

1.                  Храбрый Александр Иосифович. Численное моделирование нестационарных турбулентных течений жидкости со свободной поверхностью: диссертация... кандидата физико-математических наук: 01.02.05 / Храбрый Александр Иосифович; [Место защиты: Санкт-Петербургский государственный политехнический университет].- Санкт-Петербург, 2014.- 154 с.

2.                  Валландер С. В. Лекции по гидроаэромеханике. Учеб. пособие. Л., Изд-во Ленингр. ун-та, 1978. — 296с.

3.                  Поттер, Д. Вычислительные методы в физике / Д. Поттер. — М.: Мир, 1975.

4.                  Седов Л. И. Механика сплошной среды. Том 1. М.: Наука, 1970г. — 492с.