Ключевые слова: лагранжевы методы, эйлеровы методы, численные методы, свободная поверхность, сеточный метод, бессеточный метод, LINC, SPH, PFEM.
В работе представлено описание и сравнение существующих методов расчета потоков со свободной поверхностью, основанных на подходе Лагранжа к описанию движущихся жидкостей. Течения со свободной поверхностью играют огромную роль во многих сферах науки и техники. Определение положения поверхности раздела сред необходимо при решении многих задач инженерной гидравлики. Точное вычисление положения поверхностей такого рода, при решении сложных задач, возможно только при использовании численных методов или экспериментальным путем.
Свободная поверхность потока — граница между жидкостью и находящимся над ней газом. При решении большинства задач гидравлики открытых потоков необходимо определять форму и положение границы раздела потока движущейся жидкости. Характерными случаями такого типа являются такие нестационарные задачи как: набеганние потока жидкости на препятствие, обрушение резервуаров, плотин, подпорных стен. В качестве стационарных задач рассматриваются: истечение жидкости через затворы плотин водохранилищ, обтекание поверхностей водосливов и опор мостов, движение жидкостей в каналах с постоянным расходом.
Существует множество методов расчета течений, в которых используются разные способы определения положения свободной поверхности потока жидкости. По способу преобразования уравнений движения среды, различные численные алгоритмы решения гидравлических задач о движении жидкостей с открытой поверхностью можно разделить на 2 вида: на лагранжевы и эйлеровы. Лагранжевы методы основаны на подходе Лагранжа к записи уравнений движения потока, эйлеровы же методы основаны на подходе Эйлера.
В лагранжевых методах положение свободной поверхности определяется либо узлами подвижной расчетной сетки, либо частицами, переносящими материальные и динамические свойства среды. В эйлеровых методах, для определения положения свободной поверхности вводятся различные маркеры, которые движутся вместе со средой и не влияют на ее динамику. В качестве маркеров, могут выступать как точечные частицы, помещаемые вдоль свободной поверхности или в весь объем жидкости, так и пространственные маркер-функции [1].
Подход Лагранжа в описании движения относится к типу отсчётных. В некоторый выбранный начальный момент времени каждая из жидких частиц маркируется путём присвоения ей определенных значений координат в выбранный момент времени. В дальнейшем прослеживается движение каждой частицы индивидуально. При использовании такого подхода положение частицы в каждый момент времени будет зависеть от параметров a, b, c и t, которые называются переменными Лагранжа. Координаты частиц при лагранжевом подходе имеют вид [2]:
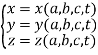 (1)
(1)
Гидродинамические величины потока являются функциями a, b, c, t [2]:
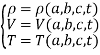 (2)
(2)
Переменные a, b, c носят название переменных Лагранжа.
Уравнение массы при использовании подхода Лагранжа имеет вид [3]:
![]() (3)
(3)
Уравнение ускорения в подходе Лагранжа примет вид [3]:
![]() (4)
(4)
Исходя из сравнения подходов Эйлера и Лагранжа [4] можно сделать вывод, что с точки зрения Лагранжа, рассматриваются законы изменения гидродинамических характеристик для выбранной точки сплошной среды, а с точки зрения Эйлера — законы изменения характеристик в выбранном месте потока жидкости.
В лагранжевых методах для получения дискретных аналогов уравнений гидродинамики используется набор узловых точек, перемещающихся вместе со средой. В качестве точек могут быть использованы узлы расчетной сетки или просто точечные частицы, не связанные друг с другом сеточными линиями. При решении задач, данные узловые точки перемещаются вместе со средой и автоматически отслеживают положение границы раздела сред.
Если используемый метод основан на движении узлов расчетной сетки, то такой метод называется сеточным, если же он основан на движении точечных несвязанных частиц, то бессеточным.
Отличительной особенностью и главным достоинством сеточных лагранжевых методов является отслеживание границы раздела узлами расчетной сетки, которая может претерпевать деформацию вместе с изменением формы потока жидкости. Данная характеристика позволяет максимально точно описывать положение поверхности раздела сред и проводить учет сложных граничных условий, например, сил поверхностного натяжения. Большинство случаев практического применения лагранжевых методов, как правило, ограничено относительно простыми течениями с небольшой деформацией свободной поверхности. Для расчета сложных, сильно деформированных течений, в которых граница раздела разрушается (потоки с образованием воздушных включений, заполнение резервуаров и свободное движение струй жидкости), использование методов деформируемых сеток сопряжено со значительными сложностями или не представляется возможным. Пример использования сеточного лагранжева метода представлен на рисунке 1.
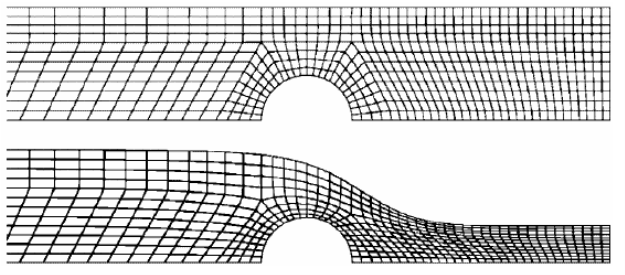
Рис. 1. Деформация сетки при расчете перетекания потока через полуцилиндр [1]
Сеточные лагранжевы методы решения задач гидравлики используют следующий алгоритм [5]:
- Формирование множества частиц в каждой подобласти;
- Идентификация границ подобласти (вследствие её возможной деформации);
- Построение новой сетки в каждой подобласти;
- Осуществление решения основных уравнений гидравлики;
- Перемещение частиц;
- Переход к следующему временному шагу и возврат к пункту 1.
Наиболее простым лагранжевым методом отслеживания положения границы раздела является метод LINC — Lagrangian Method for Incompressible Flow. Метод основан на использовании сетки, узлы которой движутся вместе с жидкостью, так что граница раздела автоматически отслеживается узлами расчетной сетки [1]. Метод LINC применим только для узкого класса задач, для которых относительная деформация элементов сетки достаточно мала, примером потока такого видя, является плавно изменяющееся движение воды перед водосливом и на его гребне.
Одним из сеточных методов, использующий сеточное лагранжево описание среды, является PFEM — метод конечных элементов с частицами. Преимуществами метода PFEM являются возможности моделирования течения жидкости со свободной поверхностью, процессов образования брызг, и потоков с высокой степенью деформации свободной поверхности. Главным недостатком такого метода является постоянное перестроение сетки на каждом шаге по времени.
В основе бессеточных лагранжевых методов лежит замена исследуемой среды набором точечных частиц, которые несут ее физические характеристики. В качестве характеристик могут выступать скорость, плотность и давление. Частицы моделируемого потока жидкости не связаны между собой линиями сетки и не ограничены в перемещении по заданному пространству. По значениям физических величин частиц, размещенных в некой области, могут быть аппроксимированы поля характеристик потока в этой области. Используя такие восстановленные поля величин, уравнения движения потока жидкости преобразовываются в уравнения, связывающие движения соседних частиц.
Наиболее распространенным методом является SPH — Smoothed Particle Hydrodynamics или «Метод сглаженных частиц». В основе метода SPH лежит дискретизация расчетной области набором лагранжевых частиц, которые можно представлять, как элементарные объёмы потока жидкости. Пространственное расстояние между частицами именуется «длиной сглаживания». Основные достоинства метода SPH — высокая точность описания конвекции и сложных течений с сильной деформацией свободной поверхности.
Метод SPH имеет следующие достоинства и недостатки [1]:
Метод позволяет легко варьировать степень точности решения и, соответственно, вычислительные затраты для различных подобластей расчетной области путем задания различной длины сглаживания;
Возможность учета сил поверхностного натяжения может быть встроена в метод;
При расчетах могут возникать проблемы, такие как: возникновение скоплений частиц и образование нефизичных пустот внутри потока жидкости;
Метод не предназначен для расчета стационарных течений;
В методе нет возможности обеспечения требуемой густоты расчетных частиц в каких-либо выбранных участках расчетной области, вследствие непрерывного движения частиц в среде жидкости. По этой причине могут возникать дополнительные сложности с точным определением пограничного слоя жидкости при контакте с твердой поверхностью, что зачастую необходимо при расчете потоков в каналах с высокой шероховатостью, с участками отрыва потока и образованием циркуляционных зон.
На основе выше представленных сведений о методах расчета потоков со свободной поверхностью, основанных на подходе Лагранжа к изучению движения жидкости можно сделать следующие выводы:
- Лагранжевы методы являются эффективными при расчете потоков со слабодеформируемой поверхностью;
- При расчете сильно деформируемых потоков лагранжевы методы становятся неэффективными;
- В отличие от эйлеровых методов, лагранжевы не позволяют выполнить сгущение расчетной сетки или числа частиц в выбранных областях, что зачастую необходимо для повышения точности расчетов.
Литература:
- Храбрый Александр Иосифович. Численное моделирование нестационарных турбулентных течений жидкости со свободной поверхностью: диссертация... кандидата физико-математических наук: 01.02.05 / Храбрый Александр Иосифович; [Место защиты: Санкт-Петербургский государственный политехнический университет].- Санкт-Петербург, 2014.- 154 с.
- Валландер С. В. Лекции по гидроаэромеханике. Учеб. пособие. Л., Изд-во Ленингр. ун-та, 1978. — 296с.
- Поттер, Д. Вычислительные методы в физике / Д. Поттер. — М.: Мир, 1975.
- Седов Л. И. Механика сплошной среды. Том 1. М.: Наука, 1970г. — 492с.
- Давыдова Е. В., Корчагова В. Н., Марчевский И. К. Использование метода конечных элементов с частицами для решения задач гидродинамики // Наука и Образование. МГТУ им. Н. Э. Баумана. Электрон. журн. 2015. № 6. С. 329–345.







