В статье рассматривается природа света, исходя из эмпирических законов его распространения, и используется представление о распространяющихся независимо друг от друга световых лучах, преломляющихся и отражающихся на границе сред с разными оптическими свойствами и прямолинейных в оптически однородных средах. Наиболее важное значение геометрическая оптика имеет для расчета и конструирования оптических приборов [2].
Геометрическая оптика описывает распространение света, используя понятие лучей или пучков, отвлекаясь от его волновой природы. Она представляет собой предельный случай волновой оптики при λ → 0. В действительности достаточно, чтобы длина волн была много меньше характерных для данной задачи линейных размеров. Она также изучает поведение световых лучей (пучков) в оптических инструментах, которые состоят из различных отражающих и преломляющих поверхностей. Лежащие в основе геометрической оптики законы отражения и преломления могут быть выведены на основе уравнений Максвелла в предельном случае λ → 0. Геометрическая оптика хотя и является приближением, она представляет огромный интерес с технической и исторической точек зрения [1].
В геометрической оптике основным понятием является луч — геометрическая линия, вдоль которой распространяется световая энергия. Основные свойства лучей: они независимы друг от друга, т. е. не взаимодействуют друг с другом, и в однородной среде распространяются прямолинейно (если ничто им не препятствует). Поверхность нормальная к лучам называется волновой поверхностью [2].
Если перед точечным источником света поместить экран с отверстием, то отверстие выделит в пространстве за экраном некоторый объем, внутри которого распространяется световая энергия, называемый — световым пучком. Он имеет вид конуса с углом раствора α, который определяется расстоянием от источника до экрана и размером отверстия (апертурная диафрагма). При α = 0 говорят о параллельном световом пучке. Представления о параллельном пучке используются широко, но следует помнить, что в действительности такие пучки не существуют — это полезная идеализация. Наблюдать можно лишь световые пучки, но не лучи, потому что световые лучи — это тоже идеализация, удобная для различных геометрических построений и расчетов. С понятием луча (пучка) связывают как энергетические характеристики, например, световой поток, так и частоту, длину волны, поляризацию и другие [1].
С точки зрения лучевой оптики каждая светящаяся точка рассматривается как вершина расходящегося пучка лучей, который называют гомоцентрическим, т. е. имеющим общий центр. Если после отражения и преломления этот пучок превращается в пучок, сходящийся в одну точку, то последний также является гомоцентрическим, а его центр есть изображение светящейся точки. При сохранении гомоцентричности каждая точка источника дает только одну точку изображения. Такие изображения называются точечными или стигматическими. Волновая поверхность гомоцентрического пучка в однородной и изотропной среде является сферической поверхностью [2].
Если в результате отражения и преломления пучка гомоцентричность нарушается, то волновая поверхность перестает быть сферой. При этом стигматичность теряется и изображение точка уже не является точкой. Это явление называют астигмаизмом.
Основные законы геометрической оптики: закон зеркального отражения и закон преломления Снеллиуса [3].
Зеркальное отражение. Зеркальное отражение возникает всякий раз, когда плоская волна падает на гладкую плоскую поверхность, например, зеркало: свет не проходит через зеркало, а уходит от него по прямой линии. Отражение удовлетворяет следующими условиями:
а) отраженный луч лежит в плоскости падения, образованной падающим лучом и нормалью к поверхности;
б) угол отражения θ0 равен углу падения θ1 (θ0 = θ1 на Рис.1, оба угла измеряются от нормали).
Преломление, закон Снеллиуса. Пучок света определенного цвета преломляется, т. е. отклоняется от прямолинейного распространения всякий раз, когда на его пути встречается поверхность раздела двух сред с разными показателями преломления n. Величина отклонения зависит от отношения коэффициентов преломления n2/n1 (n1 — показатель преломления среды 1, из которой пучок выходит, n2- показатель преломления среды 2, в которую он входит) и от угла падения — угол между преломленным пучком и нормалью к поверхности θ2, на которую падает пучок (Рис.1). [3]
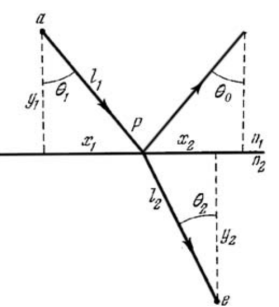
Рис. 1. Преломление и отражение света на плоской поверхности
Ниже мы покажем, что
![]() или
или ![]() (1)
(1)
где n — относительный показатель преломления. Соотношение (1) называется законом преломления Снеллиуса [1].
При явлениях преломления и отражения имеет место закон взаимности или обратимости световых лучей, который означает, что при преломлении и отражении на границе двух сред лучи остаются взаимными, т. е. при изменении направления лучей на обратное их взаимное расположение не меняется.
Литература:
- Ландсберг Г. С. Оптика. — М.: Наука, 1976. — 360 с.
- Ахманов С. Г. Физическая оптика. — М.: Наука, 2004. — 213 с.
- Бурсиан Э. В. Задачи по физике для компьютера. М.:Наука, 1991. -225 с.







