В статье рассматриваются основные аспекты вероятности безотказной работы при эксплуатации узлов контрольно-измерительных приборов (КИП) гидроэнергетических станций. Показана взаимосвязь механической и метрологической надежности, которая тесно связана со способом нормирования и законом распределения погрешностей.
Ключевые слова:гидротехника, вероятность безотказной работы, датчики и преобразователи, механическая надежность,метрологическая надежность КИП.
Автоматизация и контроль в таких важных отраслях народного хозяйства Республики Узбекистан, как гидромелиорация, гидротехника, гидроэлектрические станции, системы водного хозяйства и водоресурсосбережение требуют применения современных, высоконадёжных датчиков и преобразователей, что позволит сэкономить большое количество оросительной воды, улучшить условия труда, повысить безопасность гидротехнических сооружений, рационально использовать водные, энергетические и материальные ресурсы.
Вероятность безотказной работы Р (t) есть вероятность того, что при эксплуатации узлов контрольно-измерительных приборов (КИП) гидроэнергетических станций (ГЭС), за определенный заданный промежуток времени не произойдет ни одного отказа. Функция Р (t) является убывающей функцией. При t = 0 Р (0) = 1, а при t = ∞ Р (∞) = 0. Таким образом, Р(t) изменяется в пределах 0 ≤ P ≤ 1.
Вероятность безотказной работы определяется по приближенной формуле [1]:
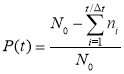
где N0 — число узлов КИП в ГЭС на начало эксплуатации; ni — число объектов, вышедших из строя; ∆t — интервал времени, в который вышли из строя объекты; t -время, для которого определяется вероятность безотказной работы.
Противоположностью вероятности безотказной работы является вероятность отказов:
По заданному Р(t)зад определяется технический ресурс. При практических расчетах вероятность безотказной работы определяется по формуле:
![]()
где n(t) — число объектов (узлов), отказавших в течение времени t. Точные формулы вероятности безотказной работы, имеют вид:
для нормального распределения
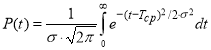 ;
;
для экспоненциального распределения
![]() ;
;
для распределения Вейбулла
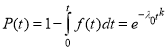 ,
,
где σ — среднее квадратичное отклонение; Тср — среднее время (математическое ожидание) наработки на отказ; λ — интенсивность отказов; k — коэффициент асимметрии распределения.
Интенсивность отказов определяется отношением
![]() ,
,
числа отказавших узлов ∆n(t) за единицу времени в интервале ∆t от t — ∆t/2 до t + ∆t/2 к среднему числу изделий продолжающих исправно работать.
![]() ,
,
здесь Ni-1и Ni — число исправно работающих объектов в конце и в начале интервала времени ∆ti. Обычно зависимость имеет три характерных участка кривой: — приработочный (до двух лет нормальной эксплуатации); — резкого износа; — старения узлов объекта.
Характер кривой интенсивности отказов зависит от эксплуатационных режимов работы объектов. Интенсивность отказов объекта выражена в виде зависимости:
![]() ,
,
где λн — интенсивность отказов для оптимальной (расчетной) нагрузки; а1 -коэффициент, учитывающий среднюю степень нагрузки объекта; зависит от отношения Кнсредней допустимой нагрузки объекта Рср за рассматриваемый период к оптимальной; а2 — коэффициент, учитывающий частоту переходных режимов (цикл/ч) за рассматриваемый период эксплуатации узла КИП в ГЭС; а3 — коэффициент, учитывающий уровень v загрузки узлов КИП в ГЭС при установившихся режимах.
Точные формулы для интенсивности отказов имеют вид:
для нормального распределения
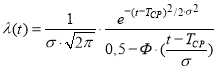 ;
;
для экспоненциального распределения
![]() ;
;
для распределения Вейбулла
![]() ,
,
где
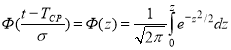
функция Гаусса или интеграл вероятностей определяется по z. Средняя наработка на отказ — среднее арифметическое время безотказной работы узла между соседними отказами:
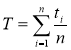
где ti — время безотказной работы между i- 1 и i отказами; n — число отказов за время эксплуатации.
Средняя наработка на отказ характеризует повторяемость отказов i узлов КИП в ГЭС при условии, что объект восстанавливается (ремонтируется). Поэтому первоначальное число узлов объекта![]() остается постоянным.
остается постоянным.
Среднее время безотказной работы
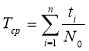
где N0 — число узлов объекта до первого отказа для заданной партии. Точная формула времени безотказной работы объектов, и имеет вид:
для нормального распределения
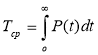 ;
;
для экспоненциального распределения
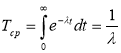 ;
;
для распределения Вейбулла
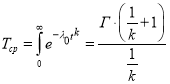 ,
,
где Г — гамма-функция.
Дисперсия случайной величины выражается:
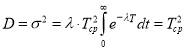 .
.
Следовательно, при экспоненциальном законе распределения среднее квадратичное отклонение σ совпадает со средним временем безотказной работы.
Частота отказов представляет собой:
![]()
т. е. отношение числа ∆nотказавших узлов объекта в интервале времени ∆t от ![]() до
до ![]() к первоначальному числу эксплуатирующихся узлов объекта N0 при условии, что отказавшие узлы не заменяются и не восстанавливаются. Частота отказов характеризует надежность насосов до их первого отказа.
к первоначальному числу эксплуатирующихся узлов объекта N0 при условии, что отказавшие узлы не заменяются и не восстанавливаются. Частота отказов характеризует надежность насосов до их первого отказа.
Точные формулы частоты отказов узлов КИП в ГЭС, имеют вид:
для нормального распределения ![]() ;
;
для экспоненциального распределения ![]() ;
;
для распределения Вейбулла ![]()
При суперпозиции нескольких законов распределения значения показателей надежности узлов КИП в ГЭС определяются по формулам:
вероятность безотказной работы ![]() ;
;
частота отказов ![]() ;
;
интенсивность отказов
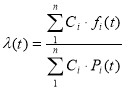 ;
;
среднее время безотказной работы ![]() ,
,
где ![]() .
.
При расчетах вероятности безотказной работы при последовательном соединении элементов, узлов КИП в ГЭС теория надежности предусматривает применение теоремы умножения вероятностей. В этом случае отказ любого из элементов вызывает отказ всей системы объекта.
![]()
При расчетах вероятности безотказной работы узлов КИП в ГЭС необходимо также учитывать, что имеется и параллельное соединение узлов, при котором отказ одного из элементов не приводит к отказу остальных элементов. Так, обозначив вероятность безотказной работы каждого узла КИП в ГЭС через РГЭС, а вероятность появления отказов через QГЭС(t), будем иметь:
![]() ;
; ![]() .
.
Очевидно, ГЭС в целом откажет в работе в том случае, если откажут все узлы, объекты КИП. Так как, вероятности безотказной работы узлов КИП являются несовместимыми событиями, то можно записать при равнонадежности объектов QГЭС = Qn, откуда:
![]()
Надежность КИП, целесообразно рассматривать в двух аспектах: механическом и метрологическом.
Механическая надежность определяется вероятностью неразрушения конструкции элементов всего преобразователя в течение заданного времени. А метрологическая надежность определяется вероятностью непревышения реальными погрешностями нормированных значений в течение заданного времени.
Расчет механической надежности ТРВ на стадии проектирования выполняется на основе структурно-функциональной схемы преобразователя. Исходными данными для расчета служат:
перечень элементов, из которых состоит преобразователь;
режимы работы элементов;
показатели надежности элементов.
Расчетные формулы для определения механической надежности хорошо известны и известны также (в основном) сведения о показателях надежности элементов преобразователей.
Характеристику механической надежности можно принять при проектировании КИП за основу, если внезапные отказы преобладают в общем количестве отказов. Однако, при эксплуатации КИП существенное значение имеют постепенные отказы и поэтому важную роль играет метрологическая надежность КИП, которое тесно связана со способом нормирования и законом распределения погрешностей, КИП как правило, работают в условиях воздействия большого числа влияющих факторов и закон распределения результирующей среднеквадратической погрешности можно считать нормальным. Согласно для заданного допустимого значения погрешности γдоп считая закон распределения реальной погрешности нормальным, можно найти вероятность непревышения погрешностями заданного значения [2]
Рн = Фл (γдоп /![]() ),
),
где, Фл — функция Лапласа.
Кроме рассмотренных составляющих надежности КИП Рмех и Рмет, можно ввести составляющую Рд, определяющую вероятность отсутствия внезапных отказов различных дополнительных элементов (соединительных контактов, пайки, провода и т. п.), тогда общая надежность ТРВ (при независимости этих составляющих) будет
Р∑ = Рмех · Рмет· Рд.
Оценка Р∑ дает следующее значение
Р∑ = 0,97.
Таким образом, приведенные данные свидетельствует о высокой надежности КИП, которая достаточна для работы в условиях гидроэнергетических систем.
Следовательно, параллельная и точная работа объектов КИП повышает надежность эксплуатации Таваксайской ГЭС в целом.
Литература:
- Мирцхулава Ц. Е. Надёжность гидромелиоративных сооружений. — М.: Колос, 1974. — 277 с.
- Ташматов Х. К. Расчет надежности теплового расходомера воды. Сборник материалов РНПК. Карши. КарГУ,2008.С.24–25.







