A qualities investigation of one group of two- dimensional systems of differential equation was realized in the study.
For this system stability conditions of singular point, disposed to the point of origin and distribution of other its singular points were achieved.
Рассмотрим систему дифференциальных уравнений
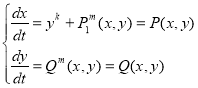 (1)
(1)
где ![]()
![]() - вещественное числа.
- вещественное числа.
Система (1) исследована в работе [2] при условии ![]() , а также в роботе [3] при
, а также в роботе [3] при ![]() .
.
Система (1) обладает следующими свойствами.
Свойство 1. Система (1) линейным невырожденным преобразованием приводится к виду
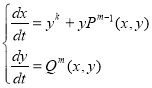 (2)
(2)
где ![]() форма степени
форма степени ![]() с вещественными коэффициентами.
с вещественными коэффициентами.
Свойство 2. При нечетном ![]() и
и ![]() система (1) инвариантна при замене
система (1) инвариантна при замене ![]() и
и ![]() на
на ![]() и
и ![]() .
.
Свойство 3. Особая точка ![]() системы (1) есть четырехсепаратрисное седло, если
системы (1) есть четырехсепаратрисное седло, если ![]() ; фокус или центр, если
; фокус или центр, если ![]()
Свойство 4. Если форма
![]() знакопостоянна, то у системы (1) в плоскости
знакопостоянна, то у системы (1) в плоскости ![]() нет замкнутых траекторий.
нет замкнутых траекторий.
Свойство 5. На каждом луче ![]() может лежать по две диаметрально противоположны особенны точек (кроме начала координат) системы (1), где
может лежать по две диаметрально противоположны особенны точек (кроме начала координат) системы (1), где ![]() - вещественный корень алгебраического уравнения
- вещественный корень алгебраического уравнения
![]()
Свойство 6. При ![]() -четное, если форма
-четное, если форма
![]()
знакопостоянна, то у системы (1) нет замкнутых траекторий в плоскости
1. Устойчивость нулевого решения
Теорема 1. Пусть ![]() нечетные числа и
нечетные числа и ![]() , или
, или ![]() , тогда нулевое решение системы (1) асимптотически устойчиво.
, тогда нулевое решение системы (1) асимптотически устойчиво.
Доказательство. Применим второй метод Ляпунова. Пусть функция Ляпунова имеет вид
![]() .
.
Тогда ![]() в силу системы (1) примет вид
в силу системы (1) примет вид
![]()
где ![]() многочлен. Знак функции
многочлен. Знак функции ![]() при малых значениях
при малых значениях ![]() определяется знаком выражения
определяется знаком выражения ![]() которое при
которое при ![]() является определенно отрицательной и нулевое решение асимптотически устойчиво.
является определенно отрицательной и нулевое решение асимптотически устойчиво.
Если ![]() или
или ![]() , то на основании теорема 5.2 [1] следует асимптотическая устойчивость нулевого решения.
, то на основании теорема 5.2 [1] следует асимптотическая устойчивость нулевого решения.
Если же ![]() , то нулевое решение неустойчиво в силу свойства 3, особая точка
, то нулевое решение неустойчиво в силу свойства 3, особая точка ![]() - неустойчивый фокус.
- неустойчивый фокус.
Неустойчивость будет также иметь место в силу теорема 6.3 [1] и в том случае, когда ![]() или
или ![]()
Пусть в системе (1)
![]() (3)
(3)
![]() является решением. Чтобы определить тип особой точки и её устойчивость, применим метод Фромера. Введем подстановку
является решением. Чтобы определить тип особой точки и её устойчивость, применим метод Фромера. Введем подстановку
![]() ,
, ![]() ,
,
Тогда имеем
![]() (4)
(4)
Обозначим степени ![]() числителя уравнения (4) через
числителя уравнения (4) через
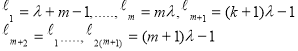
и построим на плоскости ![]() эти прямые, и находим
эти прямые, и находим ![]() .
.
При этом значении ![]() уравнение (6) примет вид
уравнение (6) примет вид
![]() (5)
(5)
где
![]() .
.
Особым точкам (0,0) и 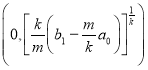 дифференциального уравнения (5) соответствуют исключительные направления
дифференциального уравнения (5) соответствуют исключительные направления ![]() (ось ох) и
(ось ох) и 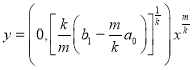 дифференциального уравнения (3). Сначала исследуем особой точки уравнения (5), определяемые из системы
дифференциального уравнения (3). Сначала исследуем особой точки уравнения (5), определяемые из системы
![]() .
.
![]() может быть узел и седло, причем здесь если
может быть узел и седло, причем здесь если ![]() ,то
,то ![]() -узел, а если
-узел, а если ![]() , то
, то![]() – седло.
– седло.
Аналогично, если ![]() , то
, то ![]() -узел, если
-узел, если ![]() , то
, то ![]() -узел, где
-узел, где 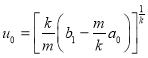 .
.
Возможны следующие неравенства
1). ![]() ,
,
2).![]() ,
,
3). ![]() ,
,
4). ![]() ,
,
5).
6). ![]() .
.
При выполнении 1), 2) исключительное направление ![]() будет 1-го, и исключительное направление
будет 1-го, и исключительное направление ![]() 2-го типа;
2-го типа;
при 3), 6) — наоборот: ![]() 2-го, а
2-го, а ![]() 1-го типа; при 4) и 5) оба исключительные направления 2-го типа.
1-го типа; при 4) и 5) оба исключительные направления 2-го типа.
Отсюда следует, что в случае ![]() начало координат для дифференциального уравнения (5) является узлом, в случае
начало координат для дифференциального уравнения (5) является узлом, в случае ![]() седлом, причем при
седлом, причем при ![]() узел устойчивый, а при
узел устойчивый, а при ![]() неустойчивый.
неустойчивый.
Т.о. имеет место:
Теорема 2. Пусть ![]() ,
, ![]() -нечетное число. Тогда нулевое решение
-нечетное число. Тогда нулевое решение ![]() системы (1) при
системы (1) при ![]() асимптотически устойчиво.
асимптотически устойчиво.
Пусть в системе (1) ![]() , и
, и ![]() -четное число, тогда дифференциальное уравнение (5) имеет три изолированы особы точек (0,0),
-четное число, тогда дифференциальное уравнение (5) имеет три изолированы особы точек (0,0), 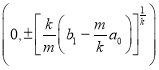 если
если ![]() , и только одну (0,0), если
, и только одну (0,0), если ![]() .
.
В силу свойства 2 особые точки ![]() будут одного типа. В данном случае, если:
будут одного типа. В данном случае, если:
1). ![]() , то (0,0) –узел,
, то (0,0) –узел, ![]() седло.
седло.
2).![]() ,то (0,0) –седло,
,то (0,0) –седло, ![]() при
при ![]() при. узлы, а при
при. узлы, а при ![]() -седла.
-седла.
3).
4). ![]() (0,0) — седло.
(0,0) — седло.
При переходе в плоскости ![]() следует отметить, что особым точкам
следует отметить, что особым точкам ![]() соответствуют исключительные направления состоящих из полупарабол, т. е. двум особым точкам
соответствуют исключительные направления состоящих из полупарабол, т. е. двум особым точкам ![]() соответствует одна парабола с осью симметрии
соответствует одна парабола с осью симметрии ![]() .
.
Т.о. имеет место:
Теорема 3. Пусть ![]() четное,
четное, ![]() , то особая точки (0,0) системы (1) является:
, то особая точки (0,0) системы (1) является:
1) при ![]() или при
или при ![]() закрытый седло-узел с одной эллиптической и одной гиперболической областью;
закрытый седло-узел с одной эллиптической и одной гиперболической областью;
2) при ![]() четырёхсепаратрисное седло;
четырёхсепаратрисное седло;
3) при ![]() закрытый узлом с двумя эллиптическими областями;
закрытый узлом с двумя эллиптическими областями;
4) При ![]() вырожденное седло.
вырожденное седло.
2. Распределение изолированных особых точек
Изучим распределение изолированных особых точек системы (1).
Форма
![]() ,
,
где ![]() корни уравнения
корни уравнения
![]() . (6)
. (6)
Отметим, что для того, чтобы все![]() различных корней уравнения (6) были вещественными необходимо и достаточно, чтобы её матрица
различных корней уравнения (6) были вещественными необходимо и достаточно, чтобы её матрица ![]() была иннорно — положительной [4]. Количество особых точек зависит от четности чисел
была иннорно — положительной [4]. Количество особых точек зависит от четности чисел ![]() и
и ![]() в системе (1).
в системе (1).
а) ![]() -четное:
-четное:
Каждая изоклина ![]() пересекается с изоклиной бесконечности
пересекается с изоклиной бесконечности
![]() (7)
(7)
в двух взаимно симметричных относительно начала точках и система может иметь ![]() изолированных особых точек.
изолированных особых точек.
б) ![]() - нечетное, то количество особых точек не более
- нечетное, то количество особых точек не более ![]() , так как каждая изоклина нуля
, так как каждая изоклина нуля ![]() пересекается с изоклиной бесконечности (7) только один раз.
пересекается с изоклиной бесконечности (7) только один раз.
Т.о. в силу свойств 1–6 имеет место:
Теорема 4. а). Пусть ![]() -нечетные числа, матрица
-нечетные числа, матрица ![]() иннорно положительна и
иннорно положительна и ![]() . Тогда система (1) имеет
. Тогда система (1) имеет ![]() изолированных особых точек, причем
изолированных особых точек, причем ![]() из них будут антиседлами, другие
из них будут антиседлами, другие ![]() -седлами и наоборот:
-седлами и наоборот: ![]() -седлами,
-седлами, ![]() -антиседлами.
-антиседлами.
Если ![]() -нечетное,
-нечетное,![]() - четное, имеет место
- четное, имеет место
в) Пусть ![]() - нечетное,
- нечетное, ![]() -четное, матрица
-четное, матрица ![]() иннорно положительна и
иннорно положительна и ![]() . Тогда система (1) имеет
. Тогда система (1) имеет ![]() -изолированных особых точек, причем возможны случаи
-изолированных особых точек, причем возможны случаи
1) ![]() -антиседел,
-антиседел, ![]() - седел.
- седел.
2) ![]() -антиседел,
-антиседел, ![]() -седло или наоборот особая точка
-седло или наоборот особая точка ![]() — вырожденное седло.
— вырожденное седло.
2.3. ![]() -четное,
-четное, ![]() нечетное. Имеет место
нечетное. Имеет место
с) Пусть ![]() -четное,
-четное, ![]() -нечетное, матрица
-нечетное, матрица ![]() иннорно-положительна и
иннорно-положительна и ![]() .Тогда система (1) имеет
.Тогда система (1) имеет ![]() изолированных особых точек, причем
изолированных особых точек, причем ![]() из них антиседел и
из них антиседел и ![]() других седел или наоборот.
других седел или наоборот. ![]() – вырожденное седло.
– вырожденное седло.
2.4. ![]() -четное. Имеет место
-четное. Имеет место
е) Пусть ![]() -четное, матрица
-четное, матрица ![]() иннорно положительна и
иннорно положительна и ![]() . Тогда система (1) имеет
. Тогда система (1) имеет ![]() изолированных особых точек, причём
изолированных особых точек, причём ![]() из них седла, а другие
из них седла, а другие ![]() -антиседла,
-антиседла, ![]() — вырожденное седло.
— вырожденное седло.
3. Распределение особых точек дифференциального уравнения (5).
Форма
![]() . (8)
. (8)
Здесь для того, чтобы все ![]() различные корни уравнения (8) были вещественными, необходимы и достаточно, чтобы её матрица
различные корни уравнения (8) были вещественными, необходимы и достаточно, чтобы её матрица ![]() была иннорно-положительной.
была иннорно-положительной.
Количество особых точек зависит от четности чисел ![]() и
и ![]() в уравнении (5).
в уравнении (5).
Исследуем дифференциальное уравнение (5) в условиях.
3.1. ![]() - нечетные. Имеет место:
- нечетные. Имеет место:
Теорема 5. Пусть матрица ![]() иннорно-положительна и
иннорно-положительна и ![]() ,тогда уравнение (5) имеет
,тогда уравнение (5) имеет ![]() изолированных особых точек, причем если
изолированных особых точек, причем если ![]()
![]() из них будут антиседлами, другие
из них будут антиседлами, другие ![]() сёдлами и наоборот
сёдлами и наоборот ![]() - седлами, другие
- седлами, другие ![]() -антиседлами, если
-антиседлами, если ![]() .
.
3.2. ![]() -нечетное,
-нечетное, ![]() -четное. Имеет место:
-четное. Имеет место:
Теорема 6. Пусть матрица ![]() иннорно — положительна и
иннорно — положительна и ![]() . Тогда дифференциальное уравнение (5) имеет
. Тогда дифференциальное уравнение (5) имеет ![]() -изолированных особых точек, причем возможны случаи:
-изолированных особых точек, причем возможны случаи:
1) ![]() -антиседла,
-антиседла, ![]() седла;
седла;
2) ![]() -антиседла,
-антиседла, ![]() седла;
седла;
3)
3.3.![]() -четное,
-четное, ![]() -нечетное. Имеет место:
-нечетное. Имеет место:
Теорема 7. Пусть матрица ![]() иннорно положительна и
иннорно положительна и ![]() . Тогда дифференциальное уравнение (5) имеет
. Тогда дифференциальное уравнение (5) имеет ![]() -изолированных особых точек, причем возможны случаи
-изолированных особых точек, причем возможны случаи ![]() -антиседла и
-антиседла и ![]() сёдел или наоборот.
сёдел или наоборот. ![]() – может быть закрытый седло узел, седло, закрытый узел. Вырожденное седло (см. Теорема 3).
– может быть закрытый седло узел, седло, закрытый узел. Вырожденное седло (см. Теорема 3).
3.4. ![]() -четные. Имеет место:
-четные. Имеет место:
Теорема 8. Пусть матрица ![]() иннорно положительна и
иннорно положительна и ![]() . Тогда дифференциальное уравнение (5) имеет
. Тогда дифференциальное уравнение (5) имеет ![]() изолированных особых точек, причем
изолированных особых точек, причем ![]() из них седла, а другие
из них седла, а другие ![]() -антиседла.
-антиседла. ![]() в силу теорема 3 может быть закрытый седло-узел, закрытый узел, седло или вырожденное седло.
в силу теорема 3 может быть закрытый седло-узел, закрытый узел, седло или вырожденное седло.
Система (1) и дифференциальное уравнение (5) исследованы при отсутствии замкнутых траекторий (см. свойство 4 и 6).
Пример. В качестве примера рассмотрим систему
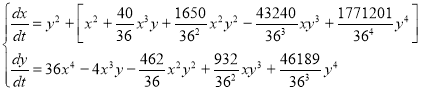
Применяя к системе преобразование ![]() , получим:
, получим:
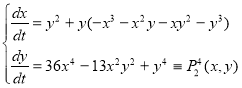
Матрица ![]() уравнения изоклины нуля
уравнения изоклины нуля ![]() иннорно положительно и функция
иннорно положительно и функция ![]() распадается на четыре линейных множителя. Кривая Шаля
распадается на четыре линейных множителя. Кривая Шаля
имеет одну действительную, два мнимых осимпты и три действительных точек перебега. Данная система имеет девять особых точек: ![]() -вырожденное седло, 4 –антиседла, 4-седла.
-вырожденное седло, 4 –антиседла, 4-седла.
Литература:
- Барбашин Е. А. Введение в теорию устойчивости. Москва. Наука. 1967 г.
- Мухтаров Я. Распределение особых точек двумерной системы специального вида. Вопросы теории дифференциальных уравнений и их приложений. Самарканд, 1989 г., ст. 22–25.
- Шарипов Ш. Р. Исследование характеристик в целом. Известия ВУЗов «Математика» № 1, 1965г.
- Джури Э. Инноры и устойчивость динамических систем. Москва, Наука, 1979г.







