Процессы формования волокнистых материалов на плоскоматричных грануляторах очень сложны и относительно мало изучены. В то же время процессы движения формуемого материала по каналу фильеры изучены достаточно подробно, но использование оборудования данного типа для формования материалов волокнистой структуры оставляет много вопросов, затрагивающих характер движения материала с учётом его физико-механических свойств, изменяющихся в процессе воздействия на них внешних сил.
При рассмотрении процессов формования большой интерес представляет определение таких показателей, как производительность машины и энергозатраты на процесс формования. При расчёте производительности плоскоматричного гранулятора большинство методов расчёта сводиться к определению пропускной способности пресс-матрицы в зависимости от плотности исходного сырья, скоростных режимов и геометрических параметров (число прессующих валков, коэффициента использования рабочей поверхности матрицы) машины.
Согласно исследованиям отечественных и зарубежных учёных основным показателем, характеризующим любой процесс уплотнения, является конечная плотность получаемых монолитов, которая повышается по мере увеличения приложенного давления [5, 6, 8]. На основании анализа полученных эмпирических зависимостей проф. Мельниковым С. В. было выведено основное уравнение (закон) прессования зернистых и волокнистых капиллярно-пористых материалов, определяющее однозначную зависимость нормального давления прессования от плотности получаемого монолита [5, 6]:
![]() ;(1)
;(1)
где С — постоянный параметр, С = b/a, (МПа);
а — параметр, характеризующий свойства материала, (м3/кг);
ρ — плотность получаемого монолита, (кг/м3);
ρ0 — плотность исходного сырья, (кг/м3).
Параметры а и С зависят от структурно-механических свойств материала (прочность, влажность, крупность частиц) и определяют собой сопротивляемость материала сжатию (определяются экспериментально).
Кучинскас З. М. в своей работе [5] определяет сопротивление прессовального канала пресса сплошного цилиндрического сечения и с конусной заходной частью как, соответственно:
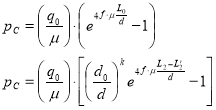 ;(2)
;(2)
где q0 —остаточное боковое давление, обусловленное упругим расширением спрессованного материала, (МПа);
μ — коэффициент бокового давления (бокового распора);
d0 — начальный диаметр заходной конической части фильеры, (м);
d — диаметр цилиндрического канала фильеры, (м);
k — коэффициент, k = 2μ·f·cosα / tgα;
f — коэффициент трения материала о стенки канала;
L2 — длина канала фильеры, (м);
L'2 — длина заходной (конической) части фильеры, (м).
Данные сопротивления каналов являются противодавлением, которое должно обеспечить максимальное давление рабочего органа для получения гранул заданной плотности.
В этой же работе определяется максимальная производительность гранулятора (т/ч) с активной плоской матрицей и коническими прессующими валками следующей зависимостью:
![]() ;(3)
;(3)
где R ‒ радиус пресс-матрицы, (м);
l — длина прессующего валка, (м);
h — подача материала на пресс-матрицу, (м);
ρ0 — начальная плотность материала, (кг/м3);
n — частота вращения пресс-матрицы, (мин -1);
z — число прессующих валков, (шт).
Ветюговым А. В. в результате исследований процесса формования тонкодисперсных порошков на грануляторе с плоской матрицей [2] было получено выражение для расчёта усилия прессования (в данном случае эта стадия предваряла стадию виброгранулирования), действующее со стороны уплотняющего катка (рис. 1), позволяющее связать между собой конструктивные, технологические параметры установки и физико-механические свойства уплотняемого материала:
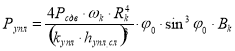 ;(4)
;(4)
где ωk — угловая скорость вращения катка, (с-1);
Pсдв — сопротивление сдвиговому деформированию слоя материала, (Н·с/м2);
Rk — радиус катка, (м);
hупл.сл — толщина слоя уплотнённого материала, (м);
kупл — коэффициент уплотнения материала;
a — расстояние от центра катка до крайней точки уплотняемого слоя, (м);
Bk — ширина катка, (м);
φ0 — угол захвата материала катком, (рад);
H0 упл — исходная толщина уплотняемого слоя, (м).
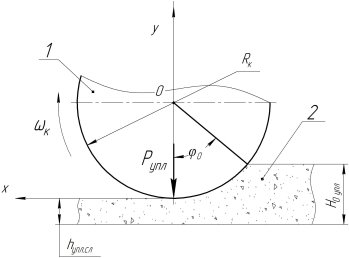
Рис. 1. Схема к расчёту процесса предуплотнения материала: 1 — каток, 2 — уплотняемый материал
В той же работе предложена формула максимальной производительности гранулятора, определяемая расходом материала через отверстия матрицы и плотностью готового продукта:
![]() ;(5)
;(5)
где ρВ — плотность продукта в зоне выдавливания в фильере матрицы, (кг/м3);
ПФ — расход материала через фильеры матрицы, (м3/с);
dотв — диаметр отверстия фильеры, (м2);
nт — частота вращения тарели, (об/мин);
z — число катков, (шт);
k — число отверстий тарели, (шт).
Необходимое условие продавливания материала через отверстия фильеры и начала процесса гранулирования является превышение вертикальных составляющих сил давления на предуплотнённый материал над силами трения:
![]() ;(6)
;(6)
где f1 — коэффициент трения между катком и материалом;
f2 — коэффициент трения между поверхностью отверстий фильеры и частицами материала;
ρ — плотность керамического порошка после предуплотнения, (кг/м3);
dотв — диаметр отверстия фильеры, (м2);
Rk — радиус прессующего катка, (м);
ωk — угловая скорость вращения катка, (с-1);
ξ — коэффициент бокового давления;
Pупл — нормальная сила (сила, действующая со стороны катка на слой материала, (Н);
h2 — высота цилиндрической части отверстия фильеры, (м);
mk — масса катка, (кг);
Fпр — нагрузка, создаваемая пружиной, (Н);
g — ускорение свободного падения, (м/с2);
Мощность, затрачиваемую на получение ранул, автор определил как:
![]() ;(7)
;(7)
где Nn.y. — мощность, затрачиваемая на равномерное распределение керамического порошка по ширине катков и его предварительное уплотнение, (Вт);
Np — мощность, затрачиваемая на прессование (продавливание через фильеру) материала, (Вт);
fк — коэффициент сопротивления качению;
Rk — радиус прессующего катка, (м).
В исследованиях Севостьянова М. В. [7] по формованию техногенных порошкообразных материалов давление, необходимое для обеспечения процесса экструдирования материала через фильеру переменного сечения (рис. 2), было определено как:
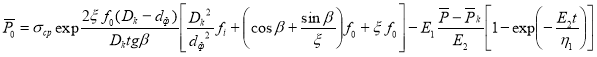 ;(8)
;(8)
где σср — среднее напряжение, действующее на элементарный слой деформируемого материала перед его истечением, (Н/м2);
ξ — коэффициент бокового давления формуемого материала;
Dк — диаметр входной конической части фильеры, (м);
dф — диаметр цилиндрической части фильеры, (м);
β — угол наклона стенок конической части фильеры к её оси, (град);
fi, f0 — коэффициенты внутреннего и внешнего трения материала;
Е1 — условно-мгновенный модуль упругости, (Н/м2);
Е2 — модуль эластичности, (Н/м2);
![]() — действующее напряжение, поддерживающее стационарный поток модулем эластичности, (Па);
— действующее напряжение, поддерживающее стационарный поток модулем эластичности, (Па);
η1 — пластическая вязкость, (Па·с);
t — единица времени, (с).
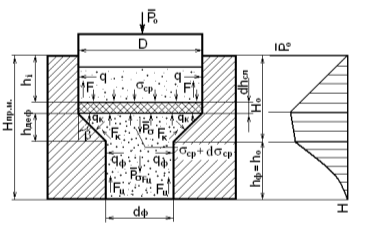
Рис. 2. Схема к расчёту давления экструдирования
Производительность агрегата и затрачиваемую, на экструдирование материала, мощность автор определил как:
![]() ;(9)
;(9)
![]() ;(10)
;(10)
где ![]() — площадь цилиндрической части фильеры, (м 2);
— площадь цилиндрической части фильеры, (м 2);
![]() — средняя скорость перемещения гранулы в фильере, (м/с);
— средняя скорость перемещения гранулы в фильере, (м/с);
ρгр — плотность сформованной гранулы, (кг/м 3);
zф — количество фильер в пресс-ватрице, (шт);
zв — количество прессующих валков, (шт);
k — коэффициент снижения производительности, (k = 0,14…0,15);
Рф — усилие, необходимое для формования гранулы в фильере, (Н);
kперем — коэффициент дополнительного сопротивления из-за наличия перемычек между фильерами, (kперем = 1,2).
В исследованиях Булатова И. А. по прессовому гранулированию мелкодисперсных сред на примере минеральных порошков и древесных отходов [1] было определено необходимое условие формования гранул, устанавливающее связь между геометрическими размерами канала матрицы и свойствами гранулируемой системы (рис. 3):
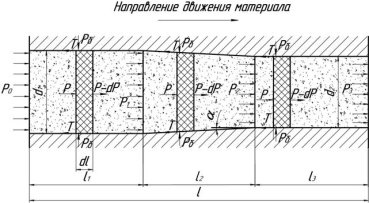
Рис. 3. Схема сил, действующих на материал в канале матрицы
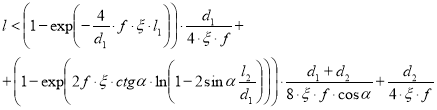 ;(11)
;(11)
где l — длина канала, (м);
l1, l2 — длина первого и второго участков канала, (м);
f — коэффициент внешнего трения;
ξ — коэффициент бокового давления;
d1, d2 — диаметры канала на первом и третьем участках, (м);
2α — угол при вершине конуса на втором участке канала, (град).
Максимальную часовую производительность гранулятора, автор работы определил исходя из скоростных режимов работы и геометрических параметров гранулятора:
![]() ;(12)
;(12)
где z — количество формующих роликов, (шт);
nmax — предельная скорость вращения вала, (об/мин);
ρнас — насыпная плотность материала, (кг/м3);
R — радиус формующего ролика, (м);
rн, rвн — радиусы поверхности матрицы, описываемые наружным и внутренним торцами ролика соответственно, (м);
αф — угол формования, (град);
СМ — константа, учитывающая реологическое состояние перерабатываемого вещества (определяется экспериментально).
В исследованиях формования древесных опилок, проводимыми Федоренчиком А. С. и Гайдукевичем Д. М. [8], для определения распределения давления по глубине х в самой фильере (рис. 4), рассматривалось равновесие элементарного слоя между двумя текущими сечениями х и х+dх, на которые действуют нормальные давления Р(х) и Р(х+dх), а равновесие достигается за счет сил трения, возникающего на боковой поверхности площадки ПDdx. В результате из уравнения баланса было получено распределение:
![]() ;(13)
;(13)
где P'ȉ δ — отношение предельного давления к атмосферному;
l — длина цилиндрической части фильеры, (м);
x — глубина распределения давления по фильере, (м);
f — коэффициент трения;
μ — модуль Пуассона для спрессованного материала;
D — диаметр цилиндрической части фильеры, (м).
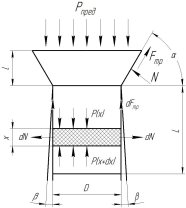
Рис. 4. Движение материала по каналу фильеры
Критерий отсутствия заклинивания, при выполнении которого спрессованный материал будет выдавливаться из фильеры, авторы выражают зависимостью:
![]() ;(14)
;(14)
где P'ȉ δ — отношение предельного давления к атмосферному;
f — коэффициент трения;
μ — модуль Пуассона для спрессованного материала.
Углы α и β (рис. 4) так же должны удовлетворять условию:
![]() ;(15)
;(15)
где P'ȉ δ — отношение предельного давления к атмосферному;
μ — модуль Пуассона для спрессованного материала;
Е — модуль Юнга для спрессованного материала.
Ковриков И. Т. и Кириленко А. С. в своих исследованиях [4] определяют производительность гранулятора зависимостью:
где ρВ — плотность продукта в зоне выдавливания из фильеры матрицы, (кг/м3);
q — число прессующих роликов, (шт);
Qф — расход материала через фильеры матрицы, (кг/м3).
При анализе приведённых выше уравнений и зависимостей можно сделать вывод о том, что при проектировании новых грануляторов экструзионного типа с плоской матрицей необходимо учитывать не только общие закономерности процесса экструдирования, но и конструктивные особенности проектируемого агрегата. Помимо этого особое внимание необходимо уделять физико-механическим и реологическим характеристикам исходных материалов и полученных из этих материалов шихт и паст.
Литература:
- Булатов, И. А. Разработка процесса прессового гранулирования мелкодисперсных сред на примере минеральных порошков и древесных отходов [Текст]: автореф. дис. канд. техн. наук / И. А. Булатов. — Москва, 2012–17с.;
- Ветюгов, А. В. Совершенствование процесса гранулирования тонкодисперсных керамических порошков [Текст]: автореф. дис. канд. техн. наук / А. В. Ветюгов. — Иваново: Изд-во ФГБОУ ВПО «ИГХТУ», 2013–16 с., с ил.;
- Глебов, Л. А. Технологическое оборудование предприятий отрасли (зерноперерабатывающие предприятия): Учебник [Текст] / Л. А. Глебов, А. Б. Демский, В. Ф. Веденьев, М. М. Темиров, Ю. М. Огурцов, 2006. — 817 с., с ил.;
- Ковриков, И. Т. Математическое моделирование рабочего процесса в вальцово-матричном пресс-грануляторе с торцевым ограничением клиновидного пространства [Текст] / И. Т. Ковриков, А. С. Кириленко // Политематический сетевой электронный научный журнал КубГАУ, № 75, 2012;
- Кучинскас, З. М. Оборудование для сушки, гранулирования и брикетировании кормов [Текст] / З. М. Кучинскас, В. И. Особов, Ю. Л. Фрегер. — М.: Агропромиздат, 1988. — 208 с., с ил.;
- Мельников, С. В. Механизация и автоматизация животноводческих ферм: Учеб. пособие высш. учебн. заведений [Текст]. / С. В. Мельников. — Л.: Колос. Ленингр. отд-ние, 1978. — 560 с., с ил.;
- Севостьянов, М. В. Пресс-валковый экструдер для формования техногенных порошкообразных материалов [Текст]: Канд. дисс. Белгород. 2006–250 с., с ил.;
- Федоренчик, А. С. Определение параметров оборудования для производства пеллет [Текст] / А. С. Федоренчик, Д. М. Гайдукевич // VIII Международный евразийский симпозиум «Деревообработка: технологии, оборудование, менеджмент XXI века». Екатеринбург. — 2013.







