При автоматизации и роботизации производства приходится определять возможность перемещения в пространстве предметов при наличии различных ограничений и решать проблему оптимальногоперемещении предметов.
Рука робота состоит из п отрезков прямых, т. е. звеньев произвольной конечной длины каждое, движущихся в евклидовой плоскости (рисунок 1).На рисунке 1 обозначено: 1 — плечо; 2 — шарнирные углы; 3 — кисть. По всей длине руки эти звенья соединены поворотными шарнирами. Один конец руки (плечо) зафиксирован, но может свободно вращаться. Другой конец руки (кисть) полностью свободен.
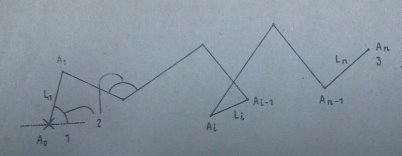
Рис. 1.
Все шарнирные связи, включая плечо и кисть, обозначены А0,А1,…,Аn. Звено между Аi-1 и Ai обозначается Li, а его длина li. Шарнирный угол между Аi, i>0 — это угол между звеньями Li и Li+1, а угол А0 — это угол звена L1 с горизонталью. Каждый шарнир все время должен находиться в пределах окружности С с центром О и радиусом r. Конфигурация руки задается положениями всех ее соединений. Переход от данной начальной конфигурации Г0 к конечной конфигурации Гf возможен в том случае, если траектория перемещения руки в Гf позволяет всем шарнирным углам изменяться с произвольными независимыми скоростями.
Рука имеет нормальную форму, если каждое соединение находится как можно ближе к С (рисунок 2). Часть руки от 
до 
называется “конечностью” шарнира Аi. Эта конечность имеет нормальную форму, если нормальную форму имеет часть руки Ai,…,Аn.Звено Liимеет левую или правую ориентацию, если центр окружности С лежит слева или справа от линии Ai — Ai-1.Если Li лежит на любом диаметре окружности, то звено Li имеет обе (левую и правую) ориентации. Переориентирование звена Li означает такое перемещение руки, при котором звено начинает менять свою существующую в данный момент ориентацию. Другими словами, переориентирование Li означает перемещение руги к такой конфигурации, при которой звено оказывается на диаметре окружности.
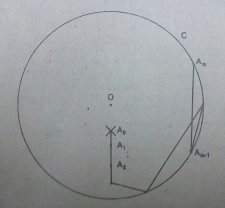
Рис. 2.
Величины сi и di означают минимальное и максимальное расстояние от С, на которых может находиться Аi.
Общий метод быстрой реконфигурации руки может позволить произвести групповое, а не индивидуальное переориентирование звеньев, у которых отличаются ориентации Г0 и Гf. Можно допустить, что А0 не лежит в центре О окружности, так как, если бы А0 находилось в центре, то реконфигурацию руки можно было бы начать с вращения относительно А0, пока А1 не займет своего предельного положения. Следовательно, конечность Аi может рассматриваться как рука робота с (n-1) звеном, изменяющая конфигурацию от плеча А1, не лежащего в центре.
Алгоритм перемещения руки в пределах окружности из конфигурации Г0 в достижимую конфигурацию Гf состоит из трех шагов.
Шаг 1. Привести руку Г0 к нормальному виду. Рассчитать последовательность перемещений, необходимых для достижения нормальной формы.
Шаг 2. Переместить руку Гn в Гn’.
Шаг 3. Используя обратную последовательность перемещений, необходимых для перехода из Гf в Гn, переместить руку в Гf.
Пусть ƶ={L1}, ориентация Liв Гn и Гn’ отличаются друг от друга. Один способ изменения Гn наГn’ заключается в перекосе каждого звена в ƶ на диаметр и в изменении ориентации обратной последовательности перемещений. Это может потребовать О(n) перемещений для каждого звена в ƶ, приводя в результате к О(n2) перемещениям. Этот результат был улучшен путем расчета подмножества ƶ так, что когда звенья этого подмножества переносятся к некоторым диаметрам, то каждый элемент из ƶ подходит к диаметру по крайней мере один раз, но не более двух раз.
Исследование переноса звена Liиз любого подмножества ƶ к диаметру окружности позволило установить, что для любого Li из ƶ существуют такие числа хi-1 и хi, при которых соблюдаются условия:
1) сi-1≤xi-1≤di-1, ci≤xi≤di;
2) 2r-xi-1-xi=liили |xi-1-xi|=li.
Всякий раз, когда шарниры Аi-1 и Aiнаходятся на расстоянии соответственно xi-1 и xi от центра окружности С, то Liдолжно лежать на диаметре.
Можно сказать, что каждый шарнир будет находиться от С на расстоянии между сi и di включительно. Когда шарниры оказываются на таких расстояниях от С, несколько шарниров, смежных с Li, будут находиться на диаметре (рисунок 3). Звенья с меньшим значением индекса называются передним покрытием (Fi), а с большим значением индекса — задним покрытием (Вi). К заднему покрытию для Li могут быть отнесены звенья, которые лежат на диаметре, когда конечность от Ai имеет нормальную форму.
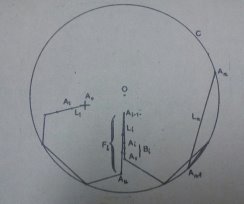
Рис. 3.
Перемещение руки к конфигурации Гd, соответствующей положению Аi-1 в xi-1 и Ai в xi,начинается от конфигурации Гn. Пусть Аu обозначает шарнир с наименьшим индексом в Fi, а Аv — шарнир с наибольшим индексом в Вi. Шарнир Аu может поворачиваться относительно фиксированного Аu-1, пока не окажется на расстоянии 
i(Au) от С, удерживая конечность от Аu все время в нормальной форме (рисунок 4). Следующее движение произойдет, когда шарнир отойдет от окружности С. Поскольку расстояние между Аu и С монотонно возрастает, то каждый шарнир отходит от С только один раз. Во время каждого движения одновременно перемещаются не более четырех звеньев. На рисунке 4, например, перемещаются только помеченные точки.
Затем аналогично, как для Аu, происходит поворот в шарнирах Аu+1,…, Аi. По окончании этой процедуры шарнир в заднем покрытии автоматически оказываются на требуемых расстояниях, так как конечность для Аi удерживалась в нормальной форме. Поскольку в требуемые позиции могут поворачиваться только | Fi|+1 шарниров и только | Fi|+| Вi|+2 шарниров отходят за все время движения от С, можно сделать вывод, что необходимо только О(| Fi|+| Вi|+1) движений и столько же этапов вычислений.
Рис. 4.
Вернем теперь руку к нормальной форме, в которой Li и звенья в покрытиях ориентированы как в Гn‘. Не имеет значения, что звенья в {Li}UFi Вi располагаются на диаметре: можно подобрать подходящую модификацию, которая обратна последовательности перемещений, использованных для приведения Li к диаметру.
Единственной проблемой для реверсирования является возможность нахождения Аi-1 или Аi в центре О для конфигурации Гd. Для упрощения предположим, что это Ai (рисунок 5) и li+1 ≤ r. Тогда необходимо Ai повернуть относительно Ai-1 в направлении, противоположном тому, из которого Ai пришло. Чтобы это осуществить, сначала Ai фиксируется в О, а затем конечность для Ai, сохраняя жесткость, поворачивается на 180°.
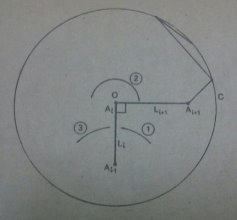
Рис. 5.
Предположим теперь, что во время О(n) вычисляется подмножество ƶ* множества ƶ так, что каждый элемент из ƶ принадлежит ƶ* либо находится в переднем или заднем покрытии элемента из ƶ*, но никогда не находится в двух передних или задних покрытиях. Используя описанную выше процедуру, каждый элемент из ƶ* приводится к диаметру и достигается конфигурация Гn’. Общее число перемещений и общее время вычислений равны ∑ik(| Fi|+| Вi|+1) каждое, де k — это некоторая константа, суммирование проводится по индексам элементов ƶ*. Эта сумма равна О(n).
Поскольку Шаги 1 и 3 также требуют О(n) перемещений и О(n) времени вычислений, на полную реконфигурацию руки потребуется только О(n) перемещений и О(n) времени вычислений.
Литература:
- Поезжаева Е. В. Промышленные роботы: учеб.пособие: в 3 ч. — Пермь: Изд-во Перм. гос. тех. ун-та,2009. — Ч. 2. — 185 с. 2.
- Козырев Ю. Г. Применение промышленных роботов. Изд-во М.: КноРус, 2011.
