При применении во многих прикладных областях робот должен оперировать различными объектами, положение и ориентация которых заранее неизвестны. В этих случаях захват объекта будет более или менее успешным в зависимости от расположения пальцев схвата на его поверхности. Поэтому важно располагать автоматическим методом оценки того, насколько удачным оказался захват объекта при данном расположении пальцев схвата.
Предлагаю метод оценки эффективности захвата, который использует модель взаимодействия схвата и объекта. Метод основан на вычислении критического значения коэффициента трения, который требуется для удержания объекта в схвате без проскальзывания при заданных внешних силах. При оценивании эффективности захвата используется тот факт, что чем меньше критический коэффициент трения, тем лучше организован захват объекта.
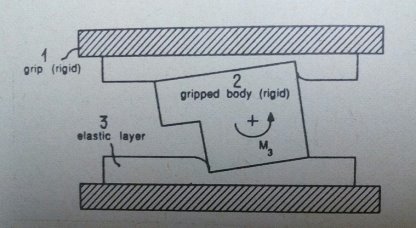
Рис. 1.
Рассматривается двупалый схват, изображенный на рисунке 1, где обозначено: 1 — схват (жесткий); 2 — объект захвата (жесткий); 3 — эластичный слой. Рабочая поверхность пальцев схвата покрыта слоем эластичного материала, например, резиной. Предполагается, что толщина этого слоя пропорциональна локальному давлению, возникающему при контакте пальца с объектом. Жесткость схвата и объекта существенно превышает жесткость эластичного слоя и может считаться абсолютной. В этих предположениях распределение давления по поверхности контакта определяется деформацией эластичного слоя. Если поверхности захватываемого объекта, приходящие в контакт с пальцами, параллельны друг другу, то давление на эластичный слой распределяется для обоих пальцев по линейным законам, в которых коэффициенты равны по абсолютной величине и противоположим по знаку. Пусть 
координаты плоскости, параллельной поверхности пальцев. Тогда давление для пальцев I и II выражается формулами
(1)
(2)
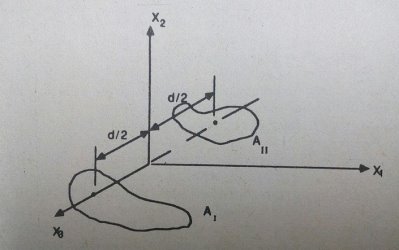
Рис. 2.
Если схват не удерживает объект в равновесии, то возникает проскальзывание объекта в схвате. Величина силы трения в каждой точке поверхности контакта равна 
или 
где 
коэффициент трения.
В начальный момент проскальзывания движение объекта относительно каждого пальца схвата представляет собой вращение вокруг оси, перпендикулярно поверхности контакта и пересекающей эту поверхность в точке с координатами
. Если бы координаты были известны, то было бы известно направление проскальзывания в каждой точке поверхности контакта. Таким образом, сила трения в каждой точке была бы определена и по направлению, так как она направлена противоположно проскальзыванию. Поэтому для определения критических условий, при которых схват удерживает объект без проскальзывания, необходимо определить семь параметров: 
Для определения перечисленных параметров следует составить семь независимых уравнений, в которые эти параметры входили бы как неизвестные.
Для составления таких уравнений вводится система координат 
как показано на рисунке 2. Здесь 
поверхности контакта, лежащие в плоскостях 
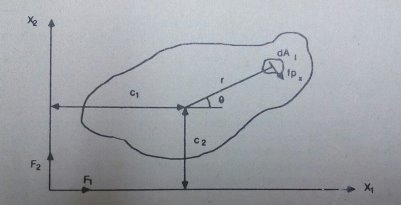
Рис. 3.
На рисунке 3 изображены внешние силы 
и момент 
действующие в плоскости контакта пальца I на объект, а также сила трения, действующая на элемент площади 
Предполагается, что в начальный момент времени вращение объекта относительно поверхности 
происходит против часовой стрелки. Суммирование сил по направлениям 
порождает равенства:
(3)
(4)
Сумма моментов относительно оси, параллельной оси 
и проходящей через 
, выражается формулой
(5)
При наличии внешних сил, не лежащих в плоскостях контакта, суммы моментов относительно осей выражаются в виде
(6)
(7)
где 
внешние моменты, действующие относительно осей 
Суммирование сил, действующих вдоль 
дает еще одно уравнение
(8)
где 
внешняя сила, действующая вдоль оси 
При отсутствии силы 
последние два слагаемых в (8) равны между собой. Они определяют силу 
которая является характеристикой схвата, так как выражает усилия, развиваемые схватом при фиксации им объекта. Для каждого схвата 
должна быть известной величиной. Отсюда возникает уравнение
(9)
После подстановки в (3–9) выражений (1,2) для 
возникает искомая система из семи уравнений от семи известных. Эти уравнения зависят от 
нелинейно и не могут быть решены алгебраическими методами. Предлагаю следующий способ решения уравнений (3–9). Формируется критерий отклонения, достигающий своего минимума при тех значениях переменных 
которые доставляют решение уравнениям (3–9). Применение методов поиска минимума к функции, выражающей критерий отклонения, позволяет получить решение уравнений (3–9) неявным образом.
Для построения критерия отклонения уравнения (3–9) приводятся к виду
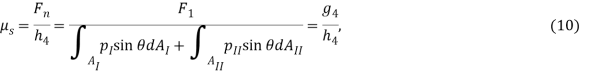
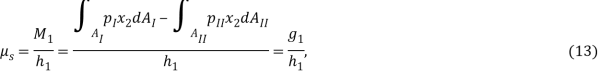
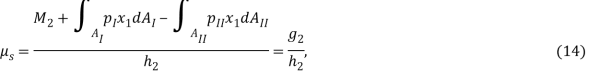
Из (10–16) можно сформировать следующий критерий отклонения
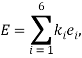(17)
Где 
весовые коэффициенты, а 
определяются формулами
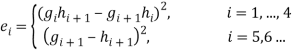(18)
Для отыскания значений переменных, доставляющих минимум критерию (17), использовал методов сопряженных направлений. Основанный на этом методе алгоритм решения уравнений (3–9) реализован на ЭВМ.
Эффективность захвата объекта обратно пропорциональна критическому коэффициенту трения 
который находится из решения уравнений (3–9). Однако при построении функции, дающей оценку эффективности захвата, следует учитывать также относительное положение и ориентацию схвата и объекта в момент фиксации объекта. Поэтому окончательно оценивать эффективность захвата предлагаю по формуле
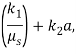
где 
параметр, характеризующий степень совпадения ориентации поверхностей пальцев и объекта.
Литература:
- Поезжаева Е. В. Промышленные роботы: учеб.пособие: в 3 ч. — Пермь: Изд-во Перм. гос. тех. ун-та,2009. — Ч. 2. — 185 с. 2.
- Поезжаева Е. В., Васенин А. С., Шумков А. Г. Роботизация фермерских хозяйств по обработке растений / Е. В. Поезжаева, А. С. Васенин, А. Г. Шумков // Научно-технический журнал «Вестник» ВСГУТУ. — 2014 — Вып. 3 — С. 59–62
- Козырев Ю. Г. Применение промышленных роботов. Изд-во: М.: КноРус, 2011.
