Параметризация процесса протекания жидкости через водослив с широким порогом

 

В предлагаемой статье рассматривается процесс параметризации процесса протекания жидкости через водосливы с широким порогом различных форм и конфигураций. Параметризация исследуемых задач в гидравлике проводится перед проведением натурных экспериментов на уменьшенных (или увеличенных) копиях сооружений. В представленной работе разработан алгоритм для поиска критериев подобия при составлении параметрического уравнения.

Ключевые слова: параметризация, поток, число Фруда, число Рейнольдса, классификация, водослив.

 

Под моделированием в широком значении этого слова понимается описание какого-то явления через его образ, эквивалентный исходному явлению (прототипу) в некотором смысле. Изучая образ реального объекта, можно получить характеристику исследуемого явления — по крайней мере в рамках принятых представлений об эквивалентности. Согласно теории подобия, основным условием, допускающим пересчет от одного процесса к другому, является равенство всех возможных взаимно независимых безразмерных комбинаций их характеристик. Комбинации этих характеристик получили название критериев подобия.

Для решения проблемы был использован полуэмпирический метод анализа размерностей, основанный на применении π-теоремы. π — теорема — основная теорема анализа размерностей. Теорема утверждает, что если имеется зависимость между n физическими величинами, не меняющая своего вида при изменении масштабов единиц в некотором классе систем единиц, то она эквивалентна зависимости между меньшим числом p=n-k безразмерных величин, где k — наибольшее число величин с независимыми размерностями среди исходных n величин. Π-теорема устанавливает общую структуру зависимости, вытекающую из требования инвариантности физической зависимости при изменении масштабов единиц, даже если конкретный вид зависимости между исходными величинами неизвестен.

На основе анализа размерностей из перечня существенных для процесса физических величин можно выделить критерии подобия, входящие в критериальное уравнение. Так называемая Пи-теорема утверждает, что число безразмерных комплексов равно числу физических величин, существенных для процесса, минус число первичных величин.

В число основных факторов, влияющих на поведение потока жидкости, были включены следующие: глубина потока жидкости в верхнем бьефе (H), ускорение свободного падения (g) и плотность рассматриваемой жидкости (ρ).

Ранее в работе А. Д. Альтшуля [1] была произведена параметризация, величины влияющие на процесс имели вид:

, (1)

где: H- глубина потока в верхнем бьефе,  — плотность жидкости, g — ускорение свободного падения,  — коэффициент динамической вязкости жидкости,  — коэффициент поверхностного натяжения, p — высота порога водослива, L — длина водослива.

Используемый А. Д. Альтшулем набор основных величин способен качественно описывать только случай свободного истечения через водослив, не учитывая условия подтопления и конструктивные особенности водослива. Исходя из данного вывода, был выполнен подбор величин, позволяющий максимально учитывать особенности каждого рассматриваемого случая. В нашем случае был добавлен параметр  — представляющий собой линейную характеристику присутствующую в рассматриваемой задаче, и  — характеризующий величину углов. Таким образом величины влияющие на процесс будут иметь вид:

(2)

Первый π -член включающий скорость подхода V будет равен:

. (3)

На основании уравнения размерностей:

. (4)

Приравнивая показатели степени при одноименных размерностях в правой и левой частях уравнения, получим систему из трех уравнений для определения показателей x,y,z:

для L: ;

для T: ;

для M: ;

Решение этой системы x=, y=0, z= позволяет получить Пи-член:

. (5)

Поступая аналогичным образом, получим остальные π-члены.

Сведя воедино все полученные критерии, подобия получим полное критериальное уравнение, характеризующее рассматриваемую задачу:

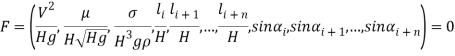(6)

Или аналогично [2]:

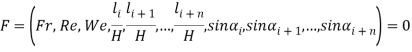(7)

где:  — число Фруда,  — число Рейнольдса,  — число Вебера.

Для определения конечного параметрического уравнения предлагается использовать следующий алгоритм подбора:

1.                Определение вида протекающей жидкости;
2.                Определение характера истечения жидкости (сводное истечение или затопленный водослив);
3.                Определение кинетических характеристик потока (скорость подхода жидкости);
4.                Определение геометрической формы водослива;
   1.            Основные характеристики (ширина, длина и высота порога);
   2.            Характеристики поперечного сечения водослива (прямоугольное, треугольное или круглое сечение);
   3.            Наличие направляющих быков и их форма;
   4.            Форма входного ребра водослива;
   5.            Наличие бокового сжатия.

Основные линейные и угловые критерии подобия для различных форм и видов водосливов сведены в таблицу 1. Основные формы и геометрические характеристики водосливов с широким порогом представлены на рисунках 1–3.

 

Таблица 1

Критерии геометрического подобия водосливов

Конструктивный элемент	Группа критериев	Название характеристики	Обозначение критерия подобия
Гребень водослива (рис.1.)		Длина водослива	L/H
		Ширина водослива	b/H
		Высота порога водослива	p/H
		Глубина в нижнем бьефе	h/H
Поперечное сечение водослива (рис.2.)	Треугольное сечение	Угол выреза	sinφ
	Круглое сечение	Радиус кривизны поверхности дна	r/H
Направляющие быки (рис.3.)	Остроконечные быки	Ширина быка
		Угол среза быка	sinΩ
	Скругленные быки	Ширина быка
		Радиус скругления	rб/H
Входное ребро водослива (рис.1.)	Наклонное ребро	Угол наклона ребра	sinα
	Скругленное ребро	Радиус скругления ребра подхода	R/H
Боковое сжатие водослива (рис.4.)	Наклонное боковое ребро	Угол наклона ребра	sinθ
		Ширина подводящего канала	B/H
	Скругленное боковое ребро	Радиус скругления ребра	rпод/H
		Ширина подводящего канала	B/H

 

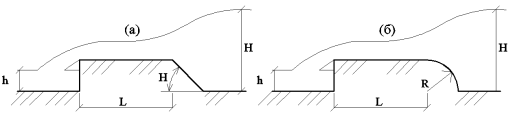
Рис. 1. Методы подвода воды к водосливу с широким порогом: а — с наклонным входным ребром, б — с скругленным входным ребром

 

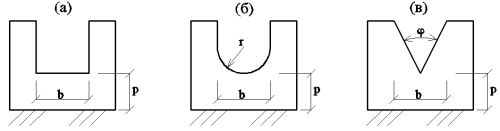
Рис. 2. Виды поперечных сечений водослива с широким порогом: а — прямоугольное сечение, б — круглое сечение, в — треугольное сечение

 

Рис. 3. Форма направляющих быков: а — остроконечная, б — скругленная

 

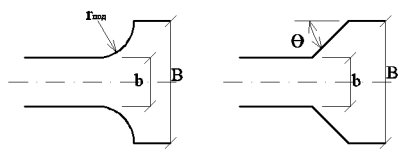
Рис. 4. Форма бокового сжатия водослива: а — с скругленным боковым ребром, б — с наклонным ребром

 

Результатом проведенных исследований является метод получения полного параметрического уравнения, позволяющего максимально точно моделировать водосливы с широким порогом. Полученное критериальное уравнение согласуется с данными А. Д. Альтшуля и имеет большее число учитываемых геометрических характеристик задачи. Представленный в статье алгоритм позволяет эффективно подбирать критерии подобия в зависимости от рассматриваемого случая.

 

Литература:

 

1.                Альтшуль А. Д. Истечение из отверстий жидкостей с повышенной вязкостью// Нефтяное хозяйство. 1950. № 2. С. 55–60.
2.                Медзвелия М. Л., Пипия В. В. Коэффициент расхода водослива с широким порогом в области малых напоров // Вестник МГСУ. 2013. № 4. С.167–171.