Results of power calculation of the eccentric cam mechanism in the environment of MathCAD are given in article.
В современных технологических машинах большое применение получили эксцентриковые кулачковые механизмы. Это вызвано, прежде веет, простотой их конструкции [1,2].
Рассмотрим кулачковый механизм эксцентрикового типа, который показан на рис.1.
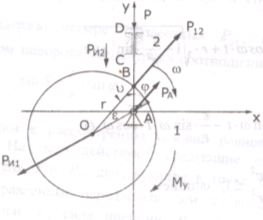
Рис. 1. Схема определения нагрузок, действующих на эксцентриковый кулачковый механизм.
Эксцентрик представляет собой диск, вращающийся с постоянной угловой скоростью ω на оси, смешенной на величину ε (эксцентриситет) от центра. Ось толкателя проходит через ось вращения эксцентрика.
Определим реакции в кинематических парах и уравновешивающий момент механизма. Положим, что нам известны следующие параметры механизма: эксцентриситетε, угловая скорость вращения ω, радиус эксцентрика r, длины l иz отрезков BC и CDсоответственно, масса толкателя т, масса эксцентрика B-, и нагрузка P.
Искомые реакции РC и PD, реакции стойки в точках C и D соответственно. Эти реакции направлены перпендикулярно к оси толкателя. Начало координат в точке А. Реакцию во вращательной кинематической паре эксцентрик-стойка обозначим через PAсилу реакции толкателя в точке В-Р21, силу реакции, эксцентрика в точке
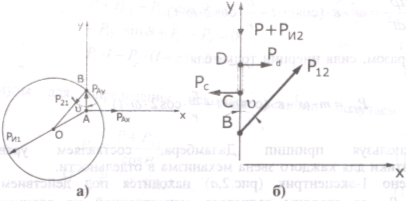
Рис. 2. Схема для определений реакций: а) в шарнире эксцентрика; б) действующих на толкатель.
Определим инерционные нагрузки, действующие на звенья механизма. Так как эксцентрик вращается равномерно с постоянной угловой скоростью, то инерционная нагрузка определяется только силой инерции звена главным вектором инерции, приложенным в центре массы эксцентрика.
Сила инерции,
![]()
Сила инерции, действующая на толкатель,
![]() ,
,
где, ρ — длина отрезка AB.
Определим величину ![]() . Полагая, что φ=0 при нижнем положении толкателя, т. е. при
. Полагая, что φ=0 при нижнем положении толкателя, т. е. при ![]() , из треугольника АОВ в соответствии с теоремой косинусов получим:
, из треугольника АОВ в соответствии с теоремой косинусов получим:
Откуда
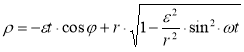 (1)
(1)
Следовательно,
![]() (2)
(2)
Имея в виду, что ![]() , запишем:
, запишем:
![]() ,
,
![]() (3)
(3)
Таким образом, сила инерции толкателя:
![]() (4)
(4)
Используя принцип Даламбера, составляем уравнения кинетостатики для каждого звена механизма в отдельности.
Звено 1-эксцентрик (рис.2,а) находится под действием сил: реакции Р21 со стороны толкателя, направленной по радиусу ОВ: реакции оси эксцентрика РА, проекции которой на оси х и у обозначаем РАx и РАy, инерционной силы Ри1. Кроме того, к эксцентрику приложен уравновешивающий момент Му.
Условие равновесия эксцентрика выражается тремя уравнениями:
![]() (5)
(5)
![]() (6)
(6)
![]() (7)
(7)
Первые два уравнения означает равенство нулю сумм сил, действующих на эксцентрик соответственно по осям х и у. Третье уравнение означает равенство нулю суммы моментов действующих сил относительно оси z, проходящей через точку А перпендикулярно плоскости чертежа.
Уравнения содержат четыре неизвестных Р21, РАх, PAy, Му. Угол υсвязан с углом поворота эксцентрика соотношением:
![]() (8)
(8)
Далее переходим к рассмотрению условий равновесия звена 2-толкателя (рис.2,б). На него действуют следующие силы: реакции направляющей толкателя Рc и Pd,действующие в точке С и точке D соответственно и направленные параллельно оси х; внешняя сила Р, направленная вдоль оси у; сила инерции Рu2, также направленная вдоль оси у; реакция эксцентрика Р12=-Р21.
Уравнения кинетостатики для звена 2 имеют вид:
![]() (9)
(9)
![]() (11)
(11)
Формулы для определения искомых величин получаем из уравнений:
![]() (12)
(12)
![]() (13)
(13)
Из уравнений (10,11) следует:
![]() (14)
(14)
![]() (15)
(15)
Из уравнений (5,6) получаем:
![]() (16)
(16)
Уравнения(1,2,3,12,13,14,15,16), решались в среде MathCAD. По результатам расчетов на ЭВМ были получены закономерности изменения перемещений, скоростей, ускорений толкателя, а также реакций в кинематических парах механизма. С целью изучения влияния угловой скорости кулачка на реакции в кинематических парах исследование проводили при вариации ω с ![]() до
до ![]() с шагом в
с шагом в ![]() . В табл.1. приведены экстремальные значения Р21, Му, Рd, Рc, РА при изменении угловой скорости кулачка.
. В табл.1. приведены экстремальные значения Р21, Му, Рd, Рc, РА при изменении угловой скорости кулачка.
Таблица 1
|
|
20 |
25 |
30 |
35 |
40 |
|
|
91,145 |
90,648 |
90,38 |
91,105 |
94,399 |
|
|
78,8 |
78,125 |
77,3 |
75,325 |
72,5 |
|
|
2,699 |
2,703 |
2,71 |
2,72 |
2,735 |
|
|
-2,699 |
-2,704 |
-2,71 |
-2,72 |
-2,735 |
|
|
162,567 |
160,661 |
158,353 |
155,62 |
152,53 |
|
|
-162,575 |
-160,675 |
-158,348 |
-155,638 |
-152,532 |
|
|
206,435 |
204,106 |
201,274 |
197,992 |
194,199 |
|
|
-206,428 |
-204,113 |
-201,291 |
-197,96 |
194,213 |
|
|
99,992 |
105,354 |
112,543 |
121,68 |
132,932 |
|
|
69,2 |
63,129 |
55,704 |
46,932 |
36,855 |
Полученные результаты позволяют произвести прочностные расчеты эксцентрика и толкателя.
Литература:
- И. И. Артоболевский, Теория механизмов и машин. М.: Наука, 1988, 640 с.
- А. М. Ашавский, В. Ф. Балабанов, B. C. Шейнбаум и др. Лабораторный практикум и курсовое проектирование по теории механизмов и машин с использованием ЭВМ. М.: Машиностроение, 1983. 160 с.







