Проблема оценки эффективности инвестиционных проектов с нерелевантными денежными потоками. Переход к MIRR

 

При оценке эффективности инвестиционных проектов встречаются сложности, связанные с объективностью интерпретации значений, полученных при расчёте показателей эффективности.

В данной статье излагается модифицированный способ расчета эффективности денежных вложений.

В настоящее время приняты «Методические рекомендации по оценке эффективности инвестиций и их отбору для финансирования (вторая редакция)» [1].

В них достаточно полно нашли отражение результаты научных исследований отечественных и зарубежных экономистов в области методов оценки эффективности.

По методу сопоставления разновременных денежных затрат и результатов показатели эффективности инвестиций можно классифицировать по следующим признакам [2]:

                   статические, в которых денежные потоки, возникающие в разные моменты времени, оцениваются как равноценные;

                   динамические, в которых денежные потоки, вызванные реализацией проекта, приводятся к эквивалентной основе посредством их дисконтирования, обеспечивая сопоставимость разновременных денежных потоков.

При оценке эффективности инвестиционных проектов обычно используют динамические методы оценки. Два основных из них — это чистый дисконтированный доход (чистая текущая стоимость — Net Present Value, NPV) и внутренняя норма рентабельности (Internal Rate of Return, IRR). Оба метода основаны на дисконтировании денежных потоков от проекта: NPV рассчитывает приведенную стоимость проекта при заданной ставке процента, IRR — дает представление о том, какая максимальная ставка кредита может быть принята для того, чтобы проект не был убыточным.

Чистый дисконтированный доход (чистая текущая стоимость — Net Present Value, NPV) — показывает эффективность вложения в инвестиционный проект: величину денежного потока в течение срока его реализации и приведенную к текущей стоимости (дисконтирование).

NPVс использованием прогнозируемых денежных потоков, связанных с планируемыми инвестициями, рассчитывается по следующей формуле:

(1)

где:

NPV — чистый дисконтированный доход инвестиционного проекта;

CFt(CashFlow) — денежный поток в период времени t;

IC (InvestCapital) — инвестиционный капитал, представляет собой затраты инвестора в первоначальный временном периоде;

r — ставка дисконтирования (барьерная ставка).

Показатель NPV заключается в суммировании дисконтированных чистых денежных потоков c 1 по n-ый период проекта и прибавлении к нему отрицательного денежного потока 0-го периода (инвестиций) [3]. То есть за счет положительного, либо отрицательного знака чистого денежного потока каждого периода при расчете NPV у нас осуществляется сложение, либо вычитание соответственно дисконтированного денежного потока каждого следующего периода. Какие решения могут быть приняты при различном значении NPVрассмотрим в табл. 1.

 

Таблица 1

Оценка значения NPV	Принятие решения
NPV≤0	Данный инвестиционный проект не обеспечивает покрытие будущих расходов или обеспечивает только безубыточность и его следует отклонить от дальнейшего рассмотрения
NPV>0	Проект привлекателен для инвестирования и требует дальнейшего анализа
NPV1>NPV2	Инвестиционный проект (1) более привлекателен по норме приведенного дохода, чем второй проект (2)

 

Невозможно принять решение лишь только по одному значению NPV, поскольку он показывает, как изменится величина стоимости бизнеса в денежном измерении, но не показывает относительную меру прироста по сравнению с первоначальными вложениями.

Ещё один показатель эффективности — внутренняя норма рентабельности (InternalRateofReturn, IRR) — коэффициент, показывающий максимально допустимый риск по инвестиционному проекту или минимальный приемлемый уровень доходности.

Внутренняя норма доходности равна ставке дисконтирования, при которой чистый дисконтированный доход отсутствует, то есть равен нулю:

IRR =r, при котором NPV = f(r) = 0 [4].

Рассчитывается по формуле:

(2)

где:

CFt (CashFlow) — денежный поток в период времени t;

IC (InvestCapital) — инвестиционные затраты на проект в первоначальном периоде (тоже являются денежным потоком CF0 = IC).

t — период времени.

Значение IRR также можно найти графическим методом, построив график зависимости NPV от ставки дисконтирования. Точка пересечения кривой NPV с осью абсцисс и покажет значение IRR.

Если рассмотреть график функции NPV = f (r), то возможно различное его представление в зависимости от значений коэффициента дисконтирования и знаков денежных потоков («плюс» или «минус»). Можно выделить две наиболее реальные типовые ситуации (рис. 1).

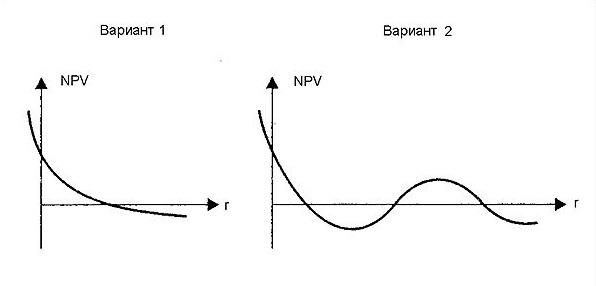
Рис.1. Возможные представления графика NPV = f (r)

 

Приведенные виды графика функции NPV = f (r) соответствуют следующим ситуациям:

                   вариант 1 — имеет место первоначальное вложение капитала с последующими поступлениями денежных средств;

                   вариант 2 — имеет место первоначальное вложение капитала, в последующие годы притоки и оттоки капитала чередуются.

Первая ситуация наиболее типична: она показывает, что функция NPV = f (r) в этом случае является убывающей с ростом r и имеет единственное значение IRR. Bo второй ситуации отток и приток капитала чередуются, что характерно для нерелевантных денежных потоков. В этом случае аналитические показатели с изменением исходных параметров могут меняться в неожиданном направлении, то есть выводы, сделанные на их основе, могут быть не всегда корректными.

В общем случае, если анализируется единственный или несколько независимых проектов с ординарным денежным потоком, когда после первоначальных затрат следуют положительные притоки денежных средств, применение критерия IRR всегда приводит к тем же результатам, что и NPV. Но в случае чередования притоков денежных средств с оттоками, для одного проекта могут существовать несколько значений IRR.

С практической точки зрения самый существенный недостаток внутренней нормы доходности — это допущение, принятое при определении всех дисконтированных денежных потоков, порожденных инвестицией, что сложные проценты рассчитываются при одной и той же процентной ставке. Для проектов, обеспечивающих нормы прибыли, близкие к барьерной ставке фирмы, проблем с реинвестициями не возникает, так как вполне разумно предположить, что существует много вариантов инвестиций, приносящих прибыль, норма которой близка к стоимости капитала. Однако для инвестиций, которые обеспечивают очень высокую или очень низкую норму прибыли, предложение о необходимости реинвестировать новые денежные поступления может исказить подлинную отдачу от проекта.

Учитывает реинвестирование денежных потоков в процессе реализации инвестиционного проекта, тем самым решая проблему IRR, модифицированная внутренняя норма рентабельности (Modified Internal Rate of Return, MIRR) [5].

Примером такого неоднократного оттока является приобретение в рассрочку или строительство объекта недвижимости, осуществляемое в течение нескольких лет.

Формула расчета модифицированной внутренней нормы доходности следующая:

(3)

где:

MIRR — внутренняя норма доходности инвестиционного проекта;

COFt — отток денежных средств в периоды времени t;

CIFt — приток денежных средств;

r — ставка дисконтирования, которая может рассчитываться как средневзвешенная стоимость капитала WACC;

d — процентная ставка реинвестирования капитала;

n — количество временных периодов.

Критерий MIRR всегда имеет единственное значение и может применяться вместо показателя IRR для оценки проектов с неординарными денежными потоками.

Методика MIRR не имеет проблемы с множественностью определения внутренней нормы доходности как у метода IRR.

На практике показатель MIRR используется редко, что нельзя считать оправданным.

IRR не всегда может быть корректно получен из уравнения NPV=0, при определенных значениях денежных потоков это уравнение может не иметь решений или иметь несколько решений. В таких ситуациях IRR проекта считается неопределенным.

Таким образом, дисконтирование затрат по безрисковой ставке дает возможность рассчитать их суммарную текущую стоимость, величина которой позволяет более объективно оценить уровень доходности инвестиций, и является более корректным методом в случае принятия инвестиционных решений с нерелевантными (неординарными) денежными потоками.

MIRR имеет значительное преимущество перед таким показателем как внутренняя норма доходности (IRR). Во-первых, при расчете модифицированной внутренней нормы доходности предполагается, что все денежные потоки будут реинвестированы по ставке дисконтирования, а не по IRR проекта. Поскольку предположение о реинвестировании по ставке стоимости капитала является более корректным, MIRR более точно характеризует его прибыльность. Во-вторых, модифицированная норма доходности может с некоторыми оговорками наравне использоваться с чистой приведенной стоимостью (NPV) при оценке взаимоисключающих проектов. Это возможно в случае, если проекты имеют одинаковые первоначальные затраты и одинаковый инвестиционный горизонт.

 

Литература:

 

1.              Методические рекомендации по оценке эффективности инвестиций и их отбору для финансирования. Официальное издание. М., 2000. 420 с.
2.              Кантор В. Е., Кантор Е. Л., Маховикова Г. А. Экономика предприятия. СПб.: Питер, 2009. 224 с.
3.              Инвестиции: учебник / А. Ю. Андрианов и др.. М.: Проспект, 2010. 584 с.
4.              Панов Л. Инвестиционное проектирование и управление проектами. Учебное пособие. СПб.: Питер, 2007. 235 с.
5.              Сухарев О. С. Инновации в экономике и промышленности. М.: Высш. шк., 2010. 317 с.