Исследованы троичные псевдослучайные последовательности на М-последовательностях и их автокорреляционные и взаимно-корреляционные функции, оценены достоинства и недостатки многофазных кодов.
Ключевые слова: код Франка, псевдослучайность, шумоподобные сигналы, фазовая модуляция, код Чу
Существуют многочисленные практические приложения, в которых периодичность используемых сигналов выдвигает на первый план качество их периодических корреляционных свойств. Эффективная периодическая АКФ играет роль вспомогательного инструмента для синтеза хороших апериодических последовательностей. Примеры с непрерывным излучением дают дальномерные системы, в особенности на больших расстояниях. Пилотный и синхронизирующий канал в цифровых системах передачи информации, радарные и сонарные системы с непрерывным излучением и т. п.
Бинарные последовательности выглядят достаточно привлекательно, обладая значительным периодическим боковым лепестком 
, который падает с ростом длины. Вероятность может быть достаточной, когда приемлемое значение 
требует относительно большой длины N. В частности, для локационных дальномерных и сонарных систем сигналов разрешение сигналов требуется в динамическом диапазоне, превышающем 80 дБ. Оптимальные бинарные последовательности длины выполняют такие условия, превышающей 
, что неоправданно замедляет начальную процедуру поиска. Очевидно, что для многих подобных сценариев наилучшим выходом могла бы служить идеальная периодическая АКФ, которая, к сожалению, недостижима на множестве бинарных кодов, наиболее привлекательных с точки зрения практической реализации. В дальнейшей части будут проанализированы возможные различные пути достижения идеальной периодической АКФ для случаев, когда алфавит последовательности не лимитирован жестким требованием бинарности символов 
. [3]
Применение недвоичной фазовой модуляции с M> 2 позволяет получить многочисленные многофазные последовательности с идеальной периодической АКФ. Существуют различные правила их конструирования, но в целом все они являются производными двух наиболее распространенных алгоритмов. Первый из них, соответствует кодам Чу (или квадратичных вычетов), аппроксимирует дискретно закон линейной частотной модуляции. Коды Чу существуют при произвольном значении длины N и формируются как
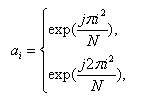,(1)
где i=…,-1,0,1,….
Легко проверить, что 
для всех i и, значит. N — по крайней мере, кратно периоду кода. В процессе вычисления периодической АКФ окончательно прояснится значение периода. Для кода четной длины ненормированная периодическая АКФ определяется в виде
При m=0modNпоследняя сумма равна N, а коэффициент, стоящий перед ней обращается в 1. Для любого другого m exp(j2πim/N)зависит от I, а упомянутая выше сумма представляет собой сумму корней из единицы некоторой степени, или. что эквивалентно, геометрической прогрессии с коэффициентом exp(j2πm/N).При вычислении суммы прогрессии, получим:
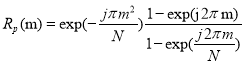
Знаменатель последней дроби никогда не обращается в нуль за исключением m=0modN и, следовательно, 
при любых сдвигах, не кратных N. Коды Чу, определяемые первой строкой в (1), обладают периодом N и имеют идеальную периодическую АКФ. Аналогичным образом осуществляется доказательство и для нечетного значения N.
Несмотря на то, что коды Чу служат достаточно убедительным академическим примером ФМ последовательностей с идеальной АКФ, их практическая реализация вызывает обоснованные сомнения, поскольку размер фазового алфавита линейно растет с увеличением длины и расстояния между соседними фазами становится чрезмерно малым. Этим обстоятельством обусловлена возрастающая требовательность к точности формирования символов кода, качеству воспроизведения фаз, условиям эксплуатации и т. п.
Аналогичные недостатки (хотя и в несколько меньшей степени) характерны для второго популярного семейства многофазных кодов: кодов Франка. Они также осуществляют пошаговую аппроксимацию линейной частотной модуляции, однако значительно более грубую, и существуют только при значениях длин, представляющих квадрат целогочисла
Правило их формирования описывается соотношением
(2)
где, как обычно, [х] обозначает округление неотрицательного х в меньшую сторону.
Доказательство идеальности периодических корреляционных свойств кодов Франка отличается незначительно и составляет суть задачи (6). Из сравнения (2) и (1) очевидно, что фазовая градация кодов Франка уменьшается 
раз.
Положим, что в дискретном многофазном сигнале число различных фаз равно p, а фазы принимают значения
(3)
Числа r и p — взаимно-простые;
-номер элемента, 
-й символ j- кодовой последовательности 
.
ВКФ сигналов j и k по определению записывается следующим образом:
(4)
Подставляя (8) в определение (9), находим
(5)
Модуль максимального пика
(6)
где 
(7)
Максимальный боковой пик будет минимальным, если максимальное значение
минимально, т. е.
=min.
Для уменьшения необходимо иметь исходные сигналы, у которых периодические АКФ имеют положительные боковые пики. Оценка ВКФ при
, (8)
где δ определяется соотношением 
Неравенству (13) удовлетворяет система кодовых последовательностей 
, символы которой определяется из сравнения второй степени:
,(9)
где 
— номер последовательности; 
-целые числа ; N-простое число. Например, при N=11, 
(10)
|
0 |
1 |
4 |
9 |
5 |
3 |
3 |
5 |
9 |
4 |
1 |
|
0 |
2 |
8 |
7 |
10 |
6 |
6 |
10 |
7 |
8 |
2 |
|
0 |
3 |
1 |
5 |
4 |
9 |
9 |
4 |
5 |
1 |
3 |
|
0 |
4 |
5 |
3 |
9 |
1 |
1 |
9 |
3 |
5 |
4 |
|
0 |
5 |
9 |
1 |
3 |
4 |
4 |
3 |
1 |
9 |
5 |
|
0 |
6 |
2 |
10 |
8 |
7 |
7 |
8 |
10 |
2 |
6 |
|
0 |
7 |
6 |
8 |
2 |
10 |
10 |
2 |
8 |
6 |
7 |
|
0 |
8 |
10 |
6 |
7 |
2 |
2 |
7 |
6 |
10 |
8 |
|
0 |
9 |
3 |
4 |
1 |
5 |
5 |
1 |
4 |
3 |
9 |
|
0 |
10 |
7 |
2 |
6 |
8 |
8 |
6 |
2 |
7 |
10 |
Каждая строка является кодовой последовательностью
. Для систем (9) при p=N периодическая АКФ каждой последовательности имеет нулевые боковые пики. Следовательно, для систем (9), (10) справедлива оценка (8)
Литература:
1. Ипатов В. Широкополосные системы и кодовое разделение сигналов. М: Техносфера, 2007,488с.
2. Варакин Л. Е. Системы связи с шумоподобными сигналами М: Радио и связь, 1985, 384с.
