В статье рассматривается структура методологического компонента физического учебного знания и модельный характер этого знания. Указывается на проблему, которая возникает при обучении, и заключается в том, что учитель физики получая это учебное знание, оформленное в виде учебника или учебного пособия, зачастую уверен в том, что получает знание об объектах реального мира — телах, реально существующих вокруг нас, а не их моделях.
Ключевые слова: методология, учебные знания, учебные модели, моделирование, модель, обучение физике.
Структура методологического компонента физического учебного знания может быть выражена следующими положениями.
- Физическая наука, как система знаний, представлена в теориях различной степени обобщенности.
- Можно выделить элементы генезиса научного знания (от предыстории до наших дней) и проблему его истинности.
- Существуют принципы научного познания (детерминизма, соответствия, дополнительности).
- Научное познание имеет уровни (теоретический и эмпирический) и методы, соответствующие каждому из этих уровней.
- Основными формами научного познания являются научный факт, проблема, гипотеза, теория.
В соответствии с требованиями современных стандартов физического образования обучающиеся должны знать методы физического познания и владеть ими. Эмпирическому уровню познания соответствуют такие методы, как наблюдение, эксперимент, измерение. К теоретическим методам исследования, соответствующим теоретическому уровню познания, относятся моделирование, идеализация, индукция и дедукция, анализ и синтез и т. д. Подобное деление весьма относительно, так как и на эмпирическом уровне при получении нового знания также могут использоваться методы, отнесенные к теоретическим. С некоторыми из них обучающиеся знакомы, и можно говорить о формирования у них умений сравнивать, анализировать, классифицировать, обобщать. Иными словами, формирование у обучающихся логического мышления приводит к возникновению у них соответствующих интеллектуальным умений. Сложнее формировать другие познавательные умения, которые необходимы в процессе научного познания и в процессе исследования для получения новых естественнонаучных знаний.
Понятие модели является очень важным. Следует отметить, что понятием модели часто заменяются другие понятия. Модельный характер имеют теория, гипотеза и проблема. Процесс моделирования, в результате которого возникает и исследуется модель объекта или явления, обладает вполне определенными функциями в самом процессе познания [5, с. 14–19].
Обычно под моделью в науке понимают заместитель изучаемого объекта, который воспроизводит его наиболее значимые свойства (в случае объекта материального мира) или закономерности (в случае явления). В теории подобным объектом может быть идеальная модель (некий умозрительный образ), математическая или символическая модель и т. п. По результатам исследования модели можно получить ответ об особенностях реального (моделируемого) объекта или явления. Теоретическая модель может быть определена как мысленно представляемая система, которая, отображая или воспроизводя объект исследования, способна замещать его так, что ее изучение дает новую информацию об этом объекте.
Для построения научной классификации моделей в качестве основания целесообразно использовать характер отношения к реальному объекту и уровень сходства модели и замещаемого образа.
По способу репрезентации, форме воспроизведения модели могут быть разделены на материальные и мысленные (идеальные) [5, с. 14]. В методологии естествознания можно особо выделить математические модели, которые являются дифференциальными и алгебраическими уравнениями. В таких случаях модель является промежуточным звеном между теорией и изучаемой реальностью, она создает возможность определения путей применения научной теории на практике, указывает пути ее возможной проверки.
Структура модельного эксперимента отличается от структуры традиционного натурного эксперимента. В натурном эксперименте объект исследования находится в непосредственном взаимодействии с другими объектами реального мира. В модельном эксперименте изучается не реальный объект, а его модель, которая подвергается воздействиям [4]. Сам объект непосредственно в эксперименте не участвует. Для модельного эксперимента характерны следующие основные операции:
переход от реального объекта к модели (моделирование);
экспериментальное исследование модели;
переход от модели обратно к реальному объекту, заключающийся в перенесении результатов, полученных при исследовании модели, на этот объект.
В работе А. C. Кондратьева и Е. В. Ситновой [6] описано положение о различии психологического состояния исследователя и преподавателя. Оно заключается в следующем. «Если для преподавателя доминирующей чертой является уверенность в правильности и надежности тех положений, которые он доносит до обучаемых, то основной чертой истинного исследователя является сомнение, которое обеспечивает возможность найти место для нового в уже устоявшейся картине физической теории или ее применения для анализа определенного явления». В этой же статье говорится о трудности сочетания этих противоположных черт у одного и того же человека. Упоминается факт, согласно которому очень редко встречаются ученые-исследователи, способные доносить новое знание своей предметной области до обучающихся и являющиеся блестящими педагогами. Предлагается разработать принципы построения методической системы, целью которой было бы формирование парадоксального характера мышления, построенного на внелогических элементах, играющих важную роль в развитии науки. Внелогические принципы не обязательно безусловно верны и «могут быть изменены при появлении новых фактов». За счет этого и происходит развитие науки. Так появляется новое знание, которое представляет собой более общую закономерность, содержащую предыдущее знание как частный случай.
Обычного школьного учителя физики нельзя сравнивать с профессиональным ученым-исследователем. Он не обладает достаточными фундаментальными знаниями и, тем не менее, должен знакомить учащихся со всеми разделами современной физики. Ученый сосредоточен на узкой области исследования, в которой он имеет почти максимальные знания, соответствующие современному этапу развития физики. Эти знания необходимо преобразовать в форму, доступную учащимся, чем обычно занимаются методисты. Знания, представленные в школьном учебнике, носят существенно приближенный характер, и, как правило, на несколько лет отстают от современных научных представлений. Таким образом, школьный учитель имеет дело с материалом, который можно считать научным, но в то же время он является существенно упрощенным и выхолощенным. Это приводит часто к тому, что учебный материал представлен в виде частного случая, так как в иной форме он просто будет недоступен для понимания обучающимся, которые не владеют соответствующим математическим аппаратом. Школьный учебник физики представляет собой некий суррогат современных физических знаний. Об этом не всегда знают или помнят (так как в педагогическом вузе им об этом должны были рассказывать) школьные учителя физики. В результате это приводит к тому, что они забывают о том, как были получены эти приближенные представления о физических объектах, имеющие модельный (упрощенный) характер, и начинают их отождествлять с реальными свойствами этих объектов.
Рассмотрим следующий пример. В школе изучаются колебания. Это изучение начинается с наиболее простых (в плане наглядного представления) примеров колебаний — механических колебаний. Известно, что движение колебательных систем является довольно сложным и даже его упрощенное рассмотрение предполагает решение дифференциальных уравнений. Естественно, что такое изучение невозможно в школе. Допустим, что нам надо изучить колебания какой-то реальной системы, которую можно заменить моделью — круговым математическим маятником.
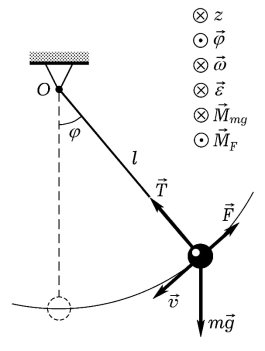
Рис. 1. Физические величины, характеризующие движение маятника с учетом силы сопротивления движению
Если на маятник массой m и длиной l будет действовать сила сопротивления движению (рис. 1), пропорциональная скорости ![]() маятника,
маятника,
то уравнение движения маятника может иметь вид:
![]() (1)
(1)
где проекция момента силы сопротивления на ось z равна
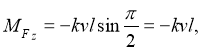
k — коэффициент сопротивления.
Скорость равна
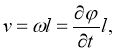
где ω — угловая скорость маятника.
Тогда уравнение (1) изменится таким образом:
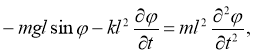
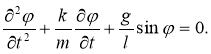 (2)
(2)
В случае малых значений φ уравнение (2) можно записать так:
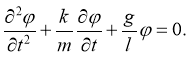 (3)
(3)
Соответствующее характеристическое уравнение
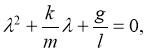
имеет корни
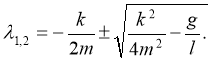
Здесь возможны три случая.
Во-первых,
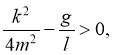
то есть
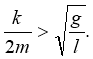
Тогда общее решение уравнения имеет вид
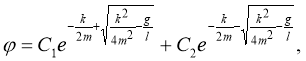 (4)
(4)
где C1 и C2 — некоторые константы. Движение, соответствующее этому решению, является апериодическим.
Во-вторых,
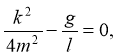
или
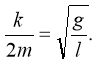
Тогда корни характеристического уравнения совпадают:
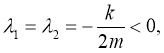
и общим решением будет
Это движение также является апериодическим.
В-третьих,
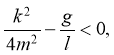
то есть
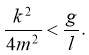
Тогда характеристическое уравнение имеет сопряженные комплексные корни с отрицательной действительной частью:
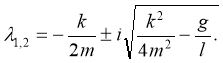
Общее решение имеет вид:
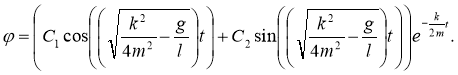 (6)
(6)
В этом случае тело совершает затухающие гармонические колебания с периодом
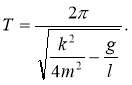 (7)
(7)
Здесь амплитуда колебаний непостоянна, а величина
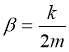 (8)
(8)
называется коэффициентом затухания. Быстроту затухания характеризует величина ![]() .
.
Однородные дифференциальные уравнения (2) и (3) описывают колебания маятника, которые называют свободными, или собственными.
В случае, когда действие силы сопротивления не учитывается, или k=0 (рис. 2), уравнение (3) приобретает вид:
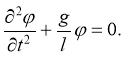
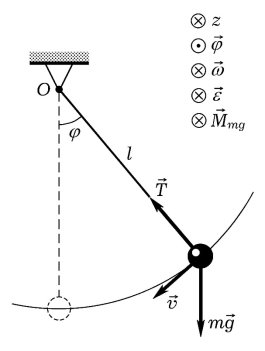
Рис. 2. Физические величины, характеризующие движение маятника без учета силы сопротивления движению
Оно может иметь решение, которое выглядит так (его можно получить, например, из уравнения (6)):
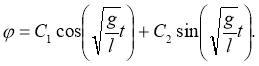
Если считать, что при t=0 угол φ= φ0, то получим следующее:
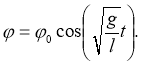
Это выражение больше знакомо обучающимся как φ = φ0 cosωt(уравнение гармонических колебаний).
Попробуем образно изобразить ситуацию, которая вполне может иметь место и демонстрирует, как модель может заменить реальный объект исследования (рис. 3). При этом речь идет не о моделировании, а о подмене представлений о реальном объекте представлениями о его модели.
Ученый-исследователь изучает объект реального мира — маятник. Стоит задача, которая заключается в том, что нужно организовать изучение его обучающимся с точки зрения современной физической теории. Исследователь понимает, что даже такой относительно простой объект представляет сложность в плане создания его адекватной модели (рис. 3; 1–3).
Современные информационные технологии позволяют автоматизировать решение многих задач (рис. 3; 4) [1; 2; 3; 7, с. 162–177], хотя в данном конкретном случае возможно и аналитическое решение без использования численных методов.
Как правило, учебные компьютерные программы сейчас используются в школе очень редко, чаще они являются не средством моделирования [1; 2; 3], а средством визуальной имитации изучаемых явлений и процессов. Это очень важный вопрос [3], требующий серьезного рассмотрения в рамках отдельной статьи, поэтому здесь подробно на нем останавливаться не будем.
В какой-то момент в процесс вмешивается методист (рис. 3; 5). Он утверждает, что и существенно упрощенное уравнение является достаточно сложным. Можно сказать, что начинается процесс замены более общей модели частной, то есть соотвествующей более частному случаю, и, тем самым, сильно ограниченной в применении (рис. 3; 6).
В результате методист получает так называемый суррогат, о котором мы говорили ранее, понимая, что в нем идет речь о модели, имеющей ограниченную область применения (рис. 3; 7). В нашем случае, это система, состоящая из идеальных объектов (материальной точки, невесомой и нерастяжимой нити), в ней отсутствую диссипативные силы, она совершает колебаний малой амплитуды и т. п. Учитель физики получая это учебное знание, оформленное в виде теоретической части учебника или учебного пособия, зачастую уверен в том, что получает знание об объектах реального мира — телах и процессах, реально существующих вокруг нас (рис. 3; 8). Кроме того, учебник содержит формулы (математические модели, полученные на самом деле путем абстрагирования и, следовательно, имеющие приближенный характер), а учителя знают, что математика — «точная» наука, откуда, по их мнению, вытекает, что они имеют точное описание движения реального объекта.
В современном стандарте школьного образования уже существуют разделы, в которых рассматриваются понятия модели и моделирования. Однако само построение учебного материала современных учебников физики и задачников не претерпело существенного изменения. Если прочесть современные задачники, то мы встретим в них автомобили, движущиеся равномерно и прямолинейно, системы отсчета, которые являются инерциальными, маятники, совершающие гармонические колебания и другие невозможные в реальном мире вещи. Решая задачи с такими текстами, школьники (а иногда и их учителя) начинают забывать, что вообще-то таких объектов (моделей или объектов физической теории) в реальном мире не существует.

Рис. 3. Процесс создания учебной модели маятника
Литература:
- Данилов О. Е. Использование компьютерной модели математического маятника при изучении механических колебаний в курсе физике / О. Е. Данилов // Молодой ученый. — 2014. — № 18. — С. 17–24.
- Данилов О. Е. Применение имитационного моделирования механических взаимодействий при обучении физике / О. Е. Данилов // Дистанционное и виртуальное обучение. — 2014. — № 5. — С. 97–103.
- Данилов О. Е. Создание систем виртуальной реальности для обучения физике / О. Е. Данилов // Дистанционное и виртуальное обучение. — 2015. — № 4 (94). — С. 20–27.
- Данилов О. Е. Сочетание натурного и вычислительного экспериментов в обучении физике / О. Е. Данилов // Молодой ученый. — 2014. — № 19. — С. 10–11.
- Зарубин В. С. Моделирование: учеб. пособие для студ. учреждений высш. проф. образования / В. С. Зарубин. — М.: Издательский центр «Академия», 2013. — 336 с.
- Кондратьев А. С. Физическое мышление на современном этапе развития науки / А. С. Кондратьев, Е. В. Ситнова // Известия Российского государственного педагогического университета им. А. И. Герцена. — № 34. — Т. 8. — 2007. — С. 7–20.
- Смирнов А. В. Методика применения информационных технологий в обучении физике: учеб. пособие для студ. высш. пед. учеб. заведений / А. В. Смирнов. — М.: Издательский центр «Академия», 2008. — 240 с.







