В данной статье рассматривается анализ движения сцены, который является одним из наиболее мощных источников информации при интерпретации изображения. Рассматриваемый анализ позволяет не только выявить и идентифицировать движущиеся объекты, но и определить трехмерную структуру сцены.
Ключевые слова: изображение, движение, кадр, свертка, оператор.
Анализ движения сцены является одним из наиболее мощных источников информации при интерпретации изображения. Такой анализ позволяет не только выявить и идентифицировать движущиеся объекты, но и определить трехмерную структуру сцены. В этой связи следует различать анализ движения объектов и движения наблюдателя. Можно выделить три уровня представления информации при анализе движения:
1) выделение движущихся частей;
2) измерение параметров движения;
3) выделение пространственной информации.
В зависимости от конкретной задачи может оказаться достаточным, например, только первый уровень иди первые два. Ниже предлагается алгоритм оценки движения, не использующий явно соответствия между кадрами последовательности.
Предлагаемый алгоритм относится к классу так называемых «градиентных схем» и основан на анализе разницы между последовательными отфильтрованными кадрами. Основными этапами алгоритма являются:
1) свертка каждого изображения последовательности с лапласианом колоколообразной (гауссовой) функции;
2) выделение точек пересечения нулевого уровня на обработанных таким образом изображениях;
3) расчет разности между парой последовательных обработанных кадров;
4) расчет компоненты скорости в направлении, перпендикулярном контурной линии;
5) грубая оценка тангенциальной компоненты скорости;
6) поиск точек пересечения нулевого уровня на втором кадре, проектирующихся из первого кадра в направлении вектора скорости.
Наряду с обычно используемыми в подобных алгоритмах ограничениями в данном случае будет сделано дополнительное допущение о том, что для медленно перемещающихся объектов (по сравнению с частотой ввод кадров) вращательные движения объекта в большинстве случаев можно представить как последовательность элементарных поступательных перемещений в пространстве. Эта гипотеза позволяет существенно упростить алгоритм, и хотя можно привести примеры ситуаций, когда она неправомочна (вращение контура вокруг центра, расположенного вблизи него или на нем), эти ситуации сравнительно редки.
На первом этапе алгоритма — этапе свертки — чрезвычайно важным является вопрос о выборе адекватного размера функции («раскрыва колокола»). Результаты расчета компоненты скорости, перпендикулярной к контурной линии, будут достаточно точными лишь в том случае, если величина смешений на последовательных изображениях будет меньше примерно половины ширины области положительных значений маски, с которой производится свертка. Поэтому, чем выше частота ввода кадров, тем уже должна быть маска, необходимая для измерения скоростей в некотором заданном диапазоне. Одна из проблем, связанных с этим фактом, состоит в том, что необходимо иметь возможность выбора оператора, наилучшим образом отвечающего скорости контурной точки. Для определения адекватности оператора ниже предлагается специальный критерий
Перпендикулярная составляющая скорости рассчитывается по формуле:
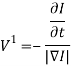
где I отфильтрованное изображение, а ![]() оператор градиента. Для определения того, адекватен ли оператор локальной скорости участка сцены, рассчитывается отношение
оператор градиента. Для определения того, адекватен ли оператор локальной скорости участка сцены, рассчитывается отношение
Если величина этого отношения окажется меньше 0,61 (которая отвечает ситуации, когда перпендикулярная компонента скорости равна половине размера маски), то данное измерение надежно. В соответствии с проведенными выше рассуждениями требуемый диапазон скоростей можно обеспечить, изменяя два параметра — частоту ввода изображений и размер фильтрующего оператора (если не считать еще фокусного расстояния объектива). Например, если частота ввода кадров составляет 70 Гц, а размер маски — 9 элементов изображения, то при таких параметрах можно измерять скорости до 315 элементов изображения в секунду.
Следующим этапом является определение истинного направления движения. Для этого принимается во внимание, что направление вектора скорости совпадает с направлением нормали к контурной линии в точке, где перпендикулярная составляющая скорости максимальна. В связи с этим рассчитывается гистограмма скоростей по каждой ориентации (суммы перпендикулярных компонент скорости для каждого направления), нормализованная по количеству контурных точек, отвечающих каждой ориентации. В случае чисто поступательного движения эта гистограмма имеет пик, соответствующий истинному направлению скорости. Описанный метод имеет недостаток, связанный с необходимостью проведения глобальных измерений по всему контуру, что не явно подразумевает, что весь контур движется в одном направлении. В большинстве случаев при больших частотах ввода это более или менее отвечает действительности. Достоинством же метода является его относительная простота и возможность быстрого получения результатов, которые можно использовать в качестве первого приближения для более точных алгоритмов. После того как направление движения определено, величину смешения можно рассчитать по перпендикулярной составляющей скорости. [1–6]
Последним этапом алгоритма является сопоставление точек пересечения нулевого уровня на двух последовательных изображениях серии. Это осуществляется с использованием информации, полученной на предыдущих этапах. Поиск осуществляется в окрестности точек нулевого уровня первого изображения пары в направлении вектора скорости, рассчитанного на предыдущем шаге. Этот этап не является обязательным для расчета параметров скорости, однако он важен при построении траекторий движущихся контуров. «Конечная точка», найденная на этом этапе, используется в качестве «начальной точки» при анализе следующего изображения серии. Таким путем удается проследить движение контура на серии изображений даже в том случае, если его форма меняется от кадра к кадру (например, вследствие изменений условий освещения).
Литература:
- Поезжаева Е. В. Промышленные роботы: учеб.пособие: в 3 ч./ Е. В. Поезжаева. — Пермь Изд-во Пермь.гос, тех. ун-та, 2006.- Ч.1.-64 с.
- Зенкевич С. Л., Ющенко А:.С. Управление роботами.- М.:Изд-во МГОУ им. Н. Э. Баумана, 2006.
- Корендясев А. И. Теоретические основы робототехники: в 2 кн./ А. И. Корендясев, Б. Л. Саламандра, Л. И. Тывес; отв. Ред. С. М. Каплунов.– М.:Наука,2006.
- Хорн Б. К. Зрение роботов.– М.:Мир,1989.
- Михайлов С. В., Романов В. В., Заикин Д. А., Система технического зрения для диагностики процесса резания материалов//Вестник компьютерных и информационных технологий, 2007, № 4, стр. 23–26
- В. И. Сырямкин, B. C. Титов, Ю. Г. Якушенков,Системы, технического зрения-МГП «РАСКО»,1992







