Приведен аналитический метод расчета индуктивного сопротивления трансформатора контактной сварки. В методе для анализа и оптимизации конструкции трансформатора контактной сварки использованы относительные единицы.
Ключевые слова: аналитический метод расчета, трансформатор, контактная сварка, индуктивное сопротивление.
The analytical method of calculation of inductive resistance of the transformer of contact welding is given. In a method for the analysis and optimization of a design of the transformer of contact welding relative units are used.
Keywords: analytical method of calculation, transformer, contact welding, inductive resistance.
В трансформаторах машин контактной сварки наиболее распространены дисковые чередующиеся обмотки. Первичные обмотки выполняются из медного провода прямоугольного сечения, а вторичные из сплошных медных дисков или из тонкостенных медных трубок, спаянных между собой. Режим работы трансформатора — повторно-кратковременный. В настоящее время разрабатываются машины контактной сварки c инверторными источниками питания, рабочая частота которых может составлять от нескольких сотен герц до десятков килогерц. В трансформаторах таких машин сильно проявляется поверхностный эффект. В настоящей статье дается аналитический метод расчета индуктивности рассеяния трансформаторов с учетом поверхностного эффекта.
На рис.1 показано сечение сварочного трансформатора с броневым магнитопроводом, четырьмя дисками 1, 3, 4, 6 первичной обмотки, выполненной из провода прямоугольного сечения, и двумя дисками 2, 5 вторичной обмотки, выполненной из медных спаянных трубок.
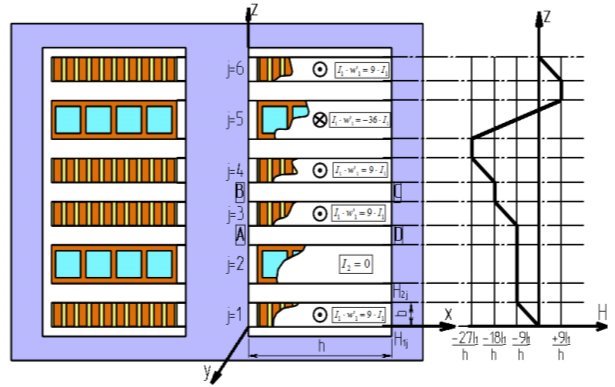
Рис. 1. К расчету потерь в обмотках сварочного трансформатора
Направления токов, протекающих в обмотках, показано точками и крестиками. Принимаем, что для магнитопровода μ→∞, тогда напряженности магнитного и электрического полей зависят только от одной координаты Z. Напряженность магнитного поля имеет только одну координату HX=H, а напряженность электрического поля одну координату EY=E. Справа на рис.1 показана эпюра напряженности магнитного поля рассеяния.
В [1] дано аналитическое выражение для активного сопротивления отдельного диска обмотки трансформатора с дисковыми обмотками. При выводе этого выражения принято, что удельная электрическая проводимость дисков первичной обмотки определяется формулой [2]:
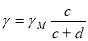(1)
где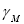 
- удельная электрическая проводимость меди, c — размер провода на рис.1, d — толщина изоляции между проводами.
Принимая во внимание сделанные допущения, необходимо рассчитать электромагнитное поле в однородном плоском проводящем листе с усредненной удельной электрической проводимостью γ, например, в листе ABCD с заданными граничными условиями H1 и H2 для напряженности магнитного поля на рис.2.
Для получения выражения для индуктивного сопротивления листа ABCD на рис.2 необходимо найти мнимую часть комплексного вектора Пойнтинга [3]. Для рассматриваемого плоского листа направления векторов Пойнтинга показано на рис.2:
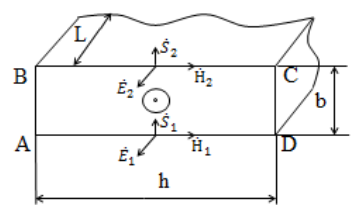
Рис. 2. К расчету электромагнитного поля в однородном плоском листе
Поэтому поток вектора Пойнтинга сквозь поверхности листа:
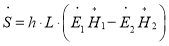(2)
где h·L — площадь боковой поверхности листа.
Для напряженности электрического поля на границе листа при Z=0 имеем:
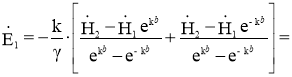
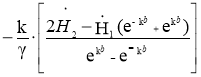(3)
где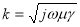 
, 
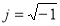, ω=2πf — угловая частота;
f — частота синусоидального напряжения трансформатора;
μ — магнитная проницаемость обмоток;
γ — удельная электрическая проводимость листа;
bj — ширина листа с номером j.
При Z=b, для напряженности электрического поля имеем:
=
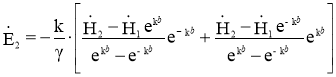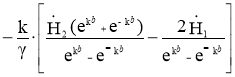(4)
Поток вектора Пойнтинга на единицу длины L листа:
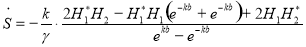(5)
Поскольку напряженности поля на границах являются действительными числами, имеем:
,
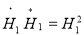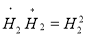(6)
Тогда выражение (2) можно записать в виде:
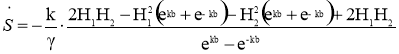(7)
Используем гиперболические функции для преобразования предыдущего и получим:
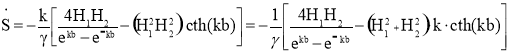(8)
Для выделения действительной и мнимой частей в комплексном векторе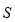 
введем безразмерный параметр 
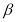— относительную толщину j-ого листа. Этот параметр характеризует степень проявления поверхностного эффекта в листе. Такой параметр используется при расчете потерь в проводниках, расположенных в пазах электрических машин, в многослойных и дисковых чередующихся обмотках трансформаторов [2]:
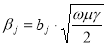(9)
Для дальнейших преобразований целесообразно представить произведение kb в виде:
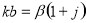(10)
Выражение для индуктивного сопротивления диска, приходящегося на единицу его длины в направлении оси OY, показанного на рис.2, имеет вид:
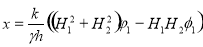(11)
где [1]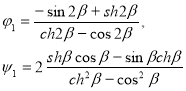 
(12)
Для удобства анализа индуктивного сопротивления введем относительную величину — отношение индуктивного сопротивления диска к сопротивлению при постоянном токе для листа ABCD:
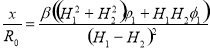(13)
где R0 — сопротивление постоянному току листа ABCD.
Это выражение можно использовать для любого диска с номером j обмоток трансформатора на рис.1:
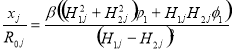(14)
Литература:
- Сахно Л. И., Сахно О. И., Лихачев Д. И. Инженерный метод расчета критической толщины дисков обмоток трансформаторов машин контактной сварки // Сварочное производство. — 2010. — № 1. — С. 17–18.
- Васютинский С. Б. Вопросы теории и расчета трансформаторов. — Л.: Энергия, 1970. — 150 с.
- Нейман Л. Р., Демирчян К. С. Теоретические основы электротехники. — Л.: Энергия, 1975. — 415 с.
