В статье рассматривается нахождения волатильности по заданной плотности распределения. Волатильность представляет собой меру риска использования финансового инструмента за заданный промежуток времени. Для решения поставленной задачи требуется решить дифференциальное уравнение в частных производных (ДУЧП).
Ключевые слова: опцион; волатильность; риск-нейтральность; дериватив.
Моделирование цен производных ценных бумаг является основой финансовой экономики и, в частности, теорий управления инвестиционным портфелем и оценки финансовых инструментов. В начале 1970-х годов Фишер Блэк (Fisher Black), Майрон Шоулз (Myron Scholes) и Роберт Мертон (Robert Merton) сделали фундаментальное открытие в теории ценообразования фондовых опционов [1, c.397]. Согласно модели Блэка-Шоулза-Мертона (БШМ), ключевым элементом определения стоимости опциона является ожидаемая волатильность базового актива. Таким образом, если известна стоимость опциона, то можно определить уровень волатильности ожидаемой рынком. На практике модель Блэка-Шоулза применяется немного не так, как это предполагали их первооткрыватели, поскольку волатильность цен может зависеть от цены акции и времени, оставшегося до истечения срока опциона. Из-за этого недостатка в модели Блэка-Шоулза, люди стремятся найти такую модель, которая включает в себя изменчивость подразумеваемой волатильности. Однако поиск новой модели до сих пор продолжается. В 1994 году известный ученый Бруно Дюпире [2, с. 128] вывел формулу, которая позволяет вычислить волатильность для европейских опционов колл. При выводе формулы Дюпире утверждается, что функция 
представляет собой плотность распределения, соответствующего рассматриваемому стохастическому дифференциальному уравнению (СДУ).
В настоящей работе предлагается построение обратной задачи определения волатильности.
Формула БШМ выглядит следующим образом:
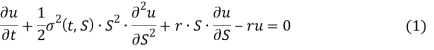
где
u(t, S) — цена любых деривативов на базовый актив S(t);
r>0 — безрисковая процентная ставка;
- волатильность.
Стоимость европейского опциона описывается следующей формулой [1, c. 450]:
где
N(d) — это интегральная функция стандартизированного нормального распределения;
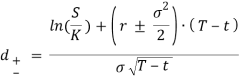
r >0 — безрисковая процентная ставка;
K — цена исполнения;
S — цена акции;
T-t — время до истечения срока опциона.
Если известна стоимость европейских опционов c(T, K) для всех сроков погашения T и всех цен-страйк K, то для функции волатильности σ справедлива формула Дюпире
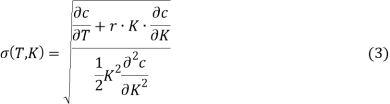
в которой для нахождения значения функции волатильности делается замена переменных T, K на переменные t, S.
Теперь рассмотрим СДУ
dS = μ ⋅ S ⋅ dt + σ ⋅ S ⋅ δ W, μ ∈ R, σ ∈ R (4)
с начальным условием
(5)
где
S — стоимость акции;
μ — ожидаемая доходность акции;
W — стандартный винеровский процесс (броуновское движение).
Пусть при 
случайная величина S(t) имеет плотность распределения 
. Начальное условие (5) для СДУ означает, что при 
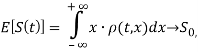
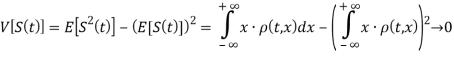
где 
— математическое ожидание и 
диссперсия.
Таким образом, плотность распределения 
должна удовлетворять следующим условиям при
Проверим выполнение этих условий для плотности логнормального распределения, возникающего в модели БШМ, а именно, когда
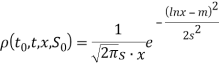
при x>0 и
=0 при x≤0,
m=ln(
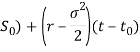, s=𝜎
Первый интеграл имеет вид
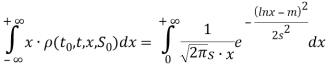
Сделаем замену переменной 
, тогда нижний и верхний пределы интегрирования по переменной 
будут равны -∞ и +∞ соответственно. Следовательно,
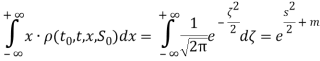
Далее
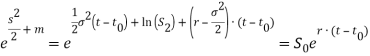
Итак, первый интеграл при
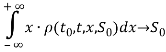
Второй интеграл имеет вид
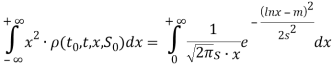
При замене переменной 
имеем 
, 
нижний и верхний пределы интегрирования по переменной ζ будут равны -∞ и +∞ соответственно. Следовательно,
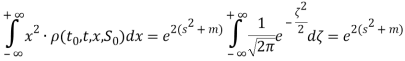
Далее
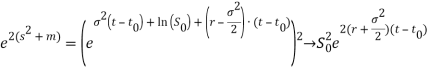
Итак, второй интеграл при
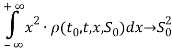
Таким образом, мы убедились, что условия (6) и (7) выполняются.
Далее рассмотрим следующую задачу: по заданной для любого t >
плотности распределения , удовлетворяющей условиям (6) и (7), найти волатильность 𝜎(t, S), для которой СДУ (4) с начальным условием (5) имеет в качестве решения случайный процесс S(t) с плотностью распределения .
Пусть c(t, S) — цена европейского опциона колл на актив S(t), тогда c(t, S) удовлетворяет уравнению (1) при этом в риск-нейтральном мире,
т. е.
или
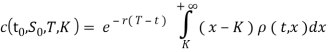
по формуле Дюпире (3) стоимость опциона 
и плотность 
связаны соотношением
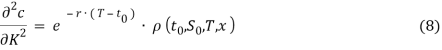
Для решения поставленной задачи нужно решить ДУЧП (8) и подставить полученные решения в формулу (3).
Общее решение уравнении с использованием формулы гомотопии [3, с. 96] может быть записано в виде:
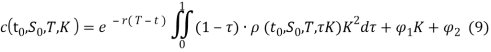
где 
— произвольные функции, не зависящие от K.
Далее, определим величины 
, 
.
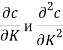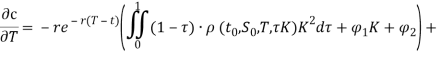
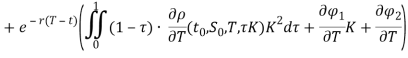
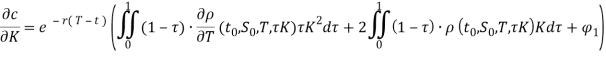
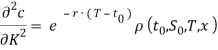
Теперь полученные значения подставляем в формулу Дюпире
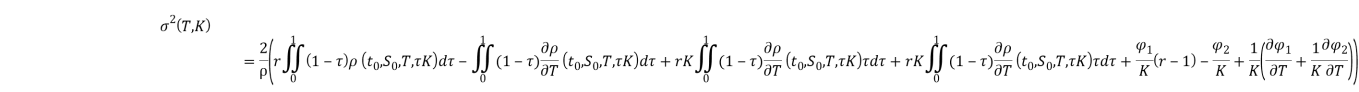
Мы получили формулу, которая позволяет нам вычислить меру риска европейского опциона колл для любого заданного распределения. Данная формула может помочь трейдерам предсказать будущее движение цен, а также определить уровень риска.
Литература:
- Джон К. Халл. Опционы, фьючерсы и другие производные финансовые инструменты, 6-е издание. ДжонК. Халл, 518стр
- Bruno Dupire. Pricing with a smile. Risk, 7(1):18–20, 1994. Reprinted in Derivative Pricing:The Classical Collection, Risk Books (2004)
- Вариационные принципы для непотенциальных операторов // Итоги науки и техники. Современные проблемы математики. Новейшие достижения. — М.: ВИНИТИ, 1992. — Т. 40. С.3 -178. (Соавторы В. М. Филиппов, В. М. Савчин).
