В статье приведены формулы для расчета эквивалентного сопротивления системы «диод — диполь», которые могут применяться при расчетах параметров радиотехнических систем.
В настоящее время устройства, осуществляющие нелинейное или параметрическое переотражение падающей электромагнитной волны находят все большее применение. Они могут быть использованы в системах радионавигации, радиопозиционирования, для создания «умных» радиопокрытий (SmartSkin). Одним из устройств такого класса является система «диод-диполь» [2, 3], которая может быть использована как электронно управляемый рассеиватель резонансной антенны.
Система «диод-диполь» представляет собой датчик типа пассивного рассеивателя, имеющий в своем составе резонансную антенну в виде полуволнового вибратора и полупроводниковый диод в качестве нагрузки. На рис. 1 показана принципиальная схема системы «диод-диполь» [3], где обозначено: 1 — полупроводниковый вибратор, 2 — полуволновый вибратор, 3 — модулятор. Работа устройства основана на электродинамических принципах управления электромагнитным полем: при параметрическом переотражении управляющее напряжение на диоде осуществляет амплитудную модуляцию отраженной волны. Таким образом, имеется возможность электронного управления ее эффективной поверхностью рассеяния. Изменяя полупроводниковые параметры [1] системы «диод-диполь» (подавая на диод управляющее напряжение, можно изменять положение рабочей точки диода, тем самым изменяя параметры, влияющие на величину эффективной поверхности рассеяния).
Как отмечено в [3], при работе на частотах до 10 ГГц маломощный полупроводниковый диод можно рассматривать как сосредоточенную нагрузку, так как ![]() , где
, где ![]() — длина волны ЭМП,
— длина волны ЭМП, ![]() — линейные размеры нагрузки.
— линейные размеры нагрузки.
Таким образом, в системе «диод-диполь» можно считать управляющим параметром сопротивление полупроводникового элемента полуволнового вибратора.
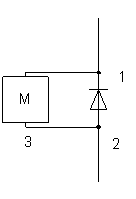
Рис. 1. Принципиальная схема системы «диод-диполь»
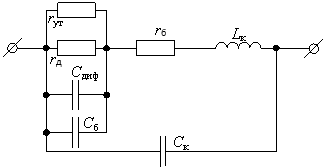
Рис. 2. Эквивалентная схема полупроводникового диода на СВЧ
В [3] предложена эквивалентная схема точечного высокочастотного диода, показанная на рис. 2, где обозначено:
rут — сопротивление утечки.
rд — дифференциальное сопротивление перехода.
rб — сопротивление базы перехода.
Cдиф — диффузионная емкость перехода.
Cб — барьерная емкость диода.
Cк — емкость корпуса и выводов диода.
Lк — индуктивность выводов и корпуса.
При использовании импульсных диодов может применяться та же эквивалентная схема [1, 3].
Если отдельно рассмотреть режимы работы диода при прямом и обратном включении диода, то приведенная на рис.2 схема может быть упрощена с учетом тех фактов, что при прямом смещении диффузионная емкость многократно преобладает над значением барьерной, следовательно, значением барьерной емкости можно пренебречь, а при обратном — емкость перехода равна барьерной емкости диода.
При прямом включении высокочастотного диода эквивалентная схема преобразуется к виду, показанному на рис. 3, в режиме обратного включения диода — на рис. 4.
Выражение для диффузионной емкости имеет вид [3]:
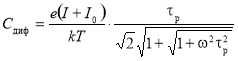 ,(1)
,(1)
где I0 — обратный ток насыщения диода, I — значение прямого тока, e — заряд электрона, ω = 2πf, f — частота тока, τр — время релаксации неосновных носителей заряда, k — постоянная Больцмана, T — абсолютная температура.
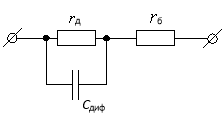
Рис. 3. Эквивалентная схема точечного диода при прямом смещении

Рис. 4. Эквивалентная схема точечного диода при обратном смещении
Дифференциальное сопротивление можно вычислить по формуле [3]:
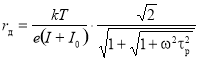 .
.
Сопротивление базы можно принять равным [3]
![]() ,
,
где r0 — радиус контакта, ρ — удельное сопротивление полупроводника.
Из схемы, представленной на рис. 3, для расчета эквивалентного сопротивления диода можно получить следующее выражение:
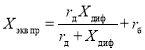 ,(2)
,(2)
где rб — сопротивление базы перехода, Xдиф — сопротивление диффузионной емкости, rд — дифференциальное сопротивление перехода.
Сопротивление диффузионной емкости Xдиф можно определить с учетом (1) по формуле:
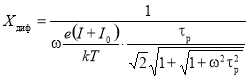 ,(3)
,(3)
С учетом (3) выражение (2) примет вид:
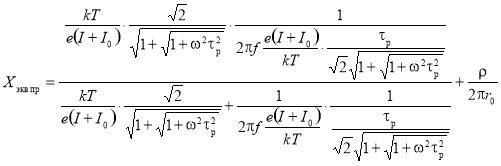 ,
,
Упростив последнее соотношение, получим выражение для расчета эквивалентного сопротивления при прямом включении диода:
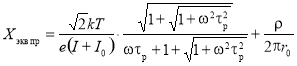 .(4)
.(4)
где k — постоянная Больцмана, T — абсолютная температура, e — заряд электрона, ω — частота тока, τр — время релаксации неосновных носителей заряда, I0 — обратный ток насыщения диода, I — значение прямого тока, ω — частота тока, r0 — радиус контакта, ρ — удельное сопротивление полупроводника.
Оценим величину эквивалентного сопротивления нагрузки в режиме обратного смещения, исходя из эквивалентной схемы полупроводникового диода при работе на отрицательной ветви вольт-амперной характеристики, показанной на рис. 4. Величина барьерной емкости при этом определяется выражением [3]:
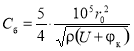 ,(5)
,(5)
где φк — контактная разность потенциалов, r0 — радиус контакта, ρ — удельное сопротивление полупроводника, U — напряжение на диоде.
Из схемы, представленной на рис. 4, для расчета эквивалентного сопротивления диода можно получить следующее выражение:
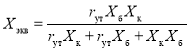 ,(6)
,(6)
где Xб — сопротивление барьерной емкости, Xк — сопротивление емкости корпуса, rут — сопротивление утечки.
За сопротивление корпуса и барьерной мощности соответственно можно принять следующие величины:
![]() ,(7)
,(7)
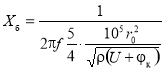 ,(8)
,(8)
где f — частота сигнала.
С учетом (5), (7) и (8) соотношение (6) примет вид:
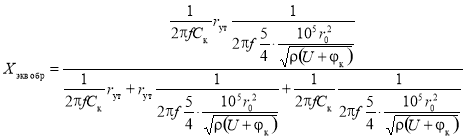 .
.
Упростив последнее выражение, получим формулу для расчета эквивалентного сопротивления диода при обратном включении:
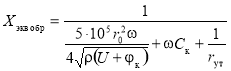 ,(9)
,(9)
где φк — контактная разность потенциалов, r0 — радиус контакта, ρ — удельное сопротивление полупроводника, U — напряжение на диоде, ω — частота тока, Cк — емкость корпуса и выводов диода, rут — сопротивление утечки.
В режиме работы при переходе через нуль сопротивление диода изменяется от (9) к (4) за время одного полупериода колебаний, подающихся на него с автогенератора.
Таким образом, при радиотехнических расчетах возможности управления пассивным рассеивателем на базе системы «диод-диполь», а также в качестве критерия при выборе полупроводникового элемента для этой системы можно использовать формулы расчета эквивалентного сопротивления (4) и (9) при прямом и обратном смещении диода соответственно.
Литература:
1. Горюнов Н. Н. Полупроводниковые диоды. Параметры, методы измерений / Н. Н. Горюнов, Ю. Р. Носов. — М.: Советское радио, 1980. — 304 с.
2. Лукин А. Н. Оптимальный приемник сигналов управляемых пассивных рассеивателей с амплитудной модуляцией [Текст] / А. Н. Лукин, А. В. Мальцев // Вестник Воронежского государственного технического университета. — 2009. — № 11. — С. 210–212.
3. Проскуряков В. Б. Повышение эффективности применения пассивных управляемых рассеивателей на базе системы «диод-диполь» [Текст]: Дисс. … канд. тех. наук. / Воронежский государственный университет. Воронеж, 2015. 121с.







