Как известно, если даны координаты концов отрезка, то можно найти координаты точки, лежащей на данном отрезке и делящей этот отрезок в данном отношении [1]. Возникает вопрос: можно ли найти уравнение прямой, делящей площадь прямоугольника в данном отношении? Данная статья затрагивает этот вопрос. Исследование данного вопроса привело к рассмотрению его в трех случаях. Во всех трех случаях мы будем рассматривать прямоугольник с вершинами в точках ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
1 случай. Найдем уравнение прямой, параллельной паре сторон ![]() и
и ![]() и делящей площадь прямоугольника в данном отношении.
и делящей площадь прямоугольника в данном отношении.
Построим на координатной плоскости прямоугольник ![]() (рис. 1).
(рис. 1).
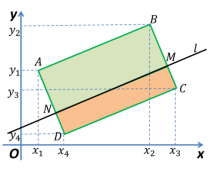
Рис. 1.
Проведем прямую ![]() так, чтобы она удовлетворяла следующим условиям (рис. 1):
так, чтобы она удовлетворяла следующим условиям (рис. 1):
1) была параллельна сторонам прямоугольника ![]() и
и ![]() ;
;
2) пересекала другие две стороны в точках ![]() и
и ![]() так, чтобы
так, чтобы
Тогда имеем, что
![]() и
и ![]() .
.
Построив данную прямую, мы поделили прямоугольник ![]() на прямоугольники
на прямоугольники ![]() и
и ![]() .
.
![]() и
и ![]() .
.
По свойству прямоугольника его противолежащие стороны равны, т. е. ![]() , следовательно
, следовательно
![]() .
.
По условию ![]() , т. е.
, т. е. ![]() . Из этого вытекает, что мы можем найти координаты точки
. Из этого вытекает, что мы можем найти координаты точки ![]() по формуле деления отрезка в данном отношении.
по формуле деления отрезка в данном отношении.
![]() .
.
Так как прямая ![]() параллельна сторонам прямоугольника, то и угловой коэффициент
параллельна сторонам прямоугольника, то и угловой коэффициент ![]() этой прямой будет такой же, как и у прямых, проходящих через эти параллельные стороны, т. е.
этой прямой будет такой же, как и у прямых, проходящих через эти параллельные стороны, т. е. ![]() .
.
Итак, мы имеем угловой коэффициент и координаты одной точки искомой прямой. Тогда мы можем составить искомое уравнение:
В частности, если ![]() , т. е. при делении площади прямоугольника
, т. е. при делении площади прямоугольника ![]() пополам (когда прямая проходит через точку пересечения диагоналей), получаем уравнение
пополам (когда прямая проходит через точку пересечения диагоналей), получаем уравнение
![]() .
.
2 случай. Найдем уравнение прямой, непараллельной сторонам, пересекающей противоположные стороны прямоугольника и делящей площадь прямоугольника в данном отношении.
Построим на координатной плоскости прямоугольник![]() (рис. 2).
(рис. 2).
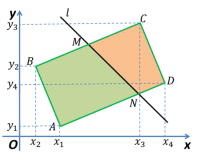
Рис. 2.
Проведем прямую ![]() так, чтобы она удовлетворяла следующим условиям (рис. 2):
так, чтобы она удовлетворяла следующим условиям (рис. 2):
1) была непараллельной сторонам прямоугольника;
2) пересекала другие стороны ![]() и
и ![]() соответственно в точках
соответственно в точках ![]() и
и ![]() так, чтобы
так, чтобы
Четырехугольники ![]() и
и ![]() являются прямоугольными трапециями, так как имеют пару параллельных сторон. Эти трапеции имеют также одинаковые высоты. Площадь трапеции определяется произведением полусуммы оснований на высоту трапеции, т. е. произведением средней линии на высоту (рис. 3). Тогда
являются прямоугольными трапециями, так как имеют пару параллельных сторон. Эти трапеции имеют также одинаковые высоты. Площадь трапеции определяется произведением полусуммы оснований на высоту трапеции, т. е. произведением средней линии на высоту (рис. 3). Тогда
![]() ;
; ![]() .
.
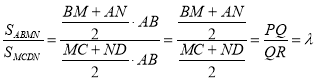 ,
,
где ![]() и
и ![]() — средние линии трапеций.
— средние линии трапеций.
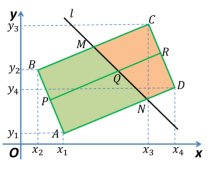
Рис. 3.
Точки ![]() и
и ![]() являются серединами сторон
являются серединами сторон ![]() и
и ![]() . Поэтому координаты этих точек можно найти, как середины отрезков, а именно:
. Поэтому координаты этих точек можно найти, как середины отрезков, а именно:
![]() ;
; ![]() ;
;
![]() ;
; ![]() .
.
Так как
![]() ;
; ![]()
Итак, мы нашли координаты точки, лежащей на искомой прямой. Осталось найти ее угловой коэффициент. Для этого докажем следующее утверждение.
Проведем через точку ![]() прямую, параллельную сторонам
прямую, параллельную сторонам ![]() и
и ![]() (рис. 4). Докажем, что отношение площадей получившихся прямоугольников
(рис. 4). Докажем, что отношение площадей получившихся прямоугольников ![]() и
и ![]() равно отношению площадей трапеций
равно отношению площадей трапеций ![]() и
и ![]() , т. е.
, т. е.
![]() .
.
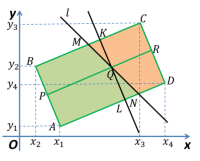
Рис. 4.
Треугольники ![]() и
и ![]() равны по двум сторонам и углу между ними, а значит они равновелики. Отсюда следует, что
равны по двум сторонам и углу между ними, а значит они равновелики. Отсюда следует, что ![]() ,
, ![]() . А это и доказывает, что
. А это и доказывает, что ![]() .
.
Из выше сказанного можно сделать следующий вывод. Какую бы прямую через ![]() мы не провели, отношение площадей получившихся трапеций будет равно отношению площадей прямоугольников
мы не провели, отношение площадей получившихся трапеций будет равно отношению площадей прямоугольников ![]() и
и ![]() . Т. е., выбирая любой угол между прямыми
. Т. е., выбирая любой угол между прямыми ![]() и
и ![]() так, чтобы условия для
так, чтобы условия для ![]() были выполнены, отношение площадей получившихся трапеций не меняется. Скажем, пусть угол между прямыми
были выполнены, отношение площадей получившихся трапеций не меняется. Скажем, пусть угол между прямыми ![]() и
и ![]() равен
равен ![]() .
.
Угловой коэффициент ![]() прямой
прямой ![]() такой же, как и у прямой
такой же, как и у прямой ![]() , так как они параллельны:
, так как они параллельны:
Угол между двумя прямыми определяется с помощью следующей формулы:
![]() .
.
где ![]() — угловой коэффициент прямой
— угловой коэффициент прямой ![]() . Отсюда с помощью небольших преобразований находим:
. Отсюда с помощью небольших преобразований находим:
![]() .
.
Итак, искомая нами прямая определяется следующим образом:
![]() .
.
В частности, если ![]() , т. е. при делении площади прямоугольника
, т. е. при делении площади прямоугольника ![]() пополам (когда прямая проходит через точку пересечения диагоналей), получается
пополам (когда прямая проходит через точку пересечения диагоналей), получается
![]() .
.
3 случай. Найдем уравнение прямой, непараллельной сторонам, пересекающей смежные стороны прямоугольника и делящей площадь прямоугольника в данном отношении.
Построим на координатной плоскости прямоугольник ![]() (рис. 5).
(рис. 5).
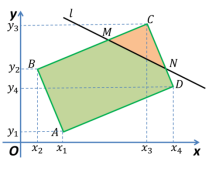
Рис. 5.
Проведем прямую ![]() так, чтобы она удовлетворяла следующим условиям (рис. 5):
так, чтобы она удовлетворяла следующим условиям (рис. 5):
1) была непараллельной сторонам прямоугольника;
2) пересекала другие стороны ![]() и
и ![]() соответственно в точках
соответственно в точках ![]() и
и ![]() так, чтобы
так, чтобы
![]() .
.
Сделаем следующие преобразования.
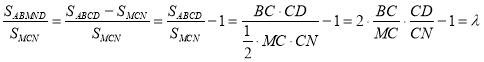 .
.
Отсюда получаем
![]()
Либо
![]() .
.
Введем следующие обозначения. Пусть
![]() ;
; ![]() .
.
Тогда мы получили уравнение с двумя переменными ![]() и
и ![]() :
:
![]() .
.
Это уравнение относительно ![]() и
и ![]() имеет бесконечно много корней. С помощью этого уравнения при фиксированном
имеет бесконечно много корней. С помощью этого уравнения при фиксированном ![]() можно найти
можно найти ![]() при следующих условиях (условия вытекают из предыдущего уравнения):
при следующих условиях (условия вытекают из предыдущего уравнения):
![]()
![]()
![]() .
.
Итак, координаты точек ![]() и
и ![]() определяются следующим образом.
определяются следующим образом.
![]() ;
; ![]() ;
;
![]() ;
; ![]() .
.
Значит, искомая наша прямая
![]() .
.
В частности, если ![]() (при этом
(при этом ![]() ,
, ![]() ), т. е. при делении площади прямоугольника
), т. е. при делении площади прямоугольника ![]() пополам, то прямая
пополам, то прямая ![]() пройдет через диагональ
пройдет через диагональ ![]() .
.
Литература:
- Бескин Н. М. Деление отрезка в данном отношении. / Бескин Н. М. — М.: Наука, 1973. — C. 64







