Мы представляем эффективный способ численного расчёта параметров мод для многослойных лазерных геометрий, основанный на матричном методе расчёта распределения электромагнитного поля [1].
Волновое уравнение, описывающее оптическую часть самосогласованной модели имеет вид:
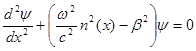 (1)
(1)
где x – координата по поперечной к слоям оси, w - частота оптического излучения, с – скорость света в вакууме, 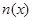 - комплексный показатель преломления,
- комплексный показатель преломления, 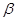 - продольная постоянная распространения,
- продольная постоянная распространения, 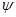 - амплитудный профиль моды.
- амплитудный профиль моды.
Особенность способа состоит в том, что собственные значения (СЗ) уравнения (1) находятся путём минимизации амплитуд "вытекающих" из волновода полей, поскольку волноводной моде всегда соответствует экспоненциально затухающий (эванесцентный) характер поля за пределами волноводной структуры. Метод отличается высокой скоростью счета. Это позволяет расширить рамки его применения на градиентные волноводы. Для расчета поперечных мод диодных лазеров недостаточно решения волноводной задачи. Пространственное распределение оптического поля в лазерной моде определяется не только геометрией волновода, но присутствием зеркал и активной среды. Диодный лазер формирует спектр излучения, тогда как в волноводе спектр излучения определяется извне. С математической точки зрения условия возбуждения мод означают, что для резонаторной задачи в уравнении (1) СЗ будут являться не постоянные распространения βj , а частоты генерации wj . Исходя из параметров резонатора, мы находим спектр комплексных частот – модовый спектр. Задача в такой постановке соответствует возможности использования кинетических уравнений, описывающих баланс фотонов и инжектированных носителей в объеме лазерного резонатора. Самосогласованная резонаторная задача в такой постановке требует нахождения модового усиления [2,3], частот и профилей лазерных мод при итерациях для нахождения параметров стационарного режима генерации.
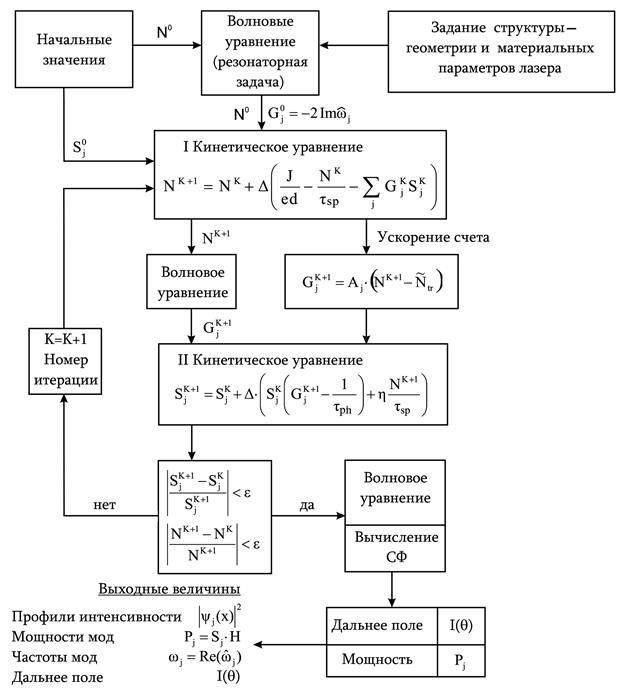
Блок схема решения самосогласованной модели приведена на рис.1
|
Рис .1. Блок схема решения самосогласованной задачи
где N- концентрация носителей в активном слое лазера, J – плотность тока накачки,
|
Как в любом автогенераторе, в лазере должны выполнятся условия самовозбуждения: баланс амплитуд и баланс фаз. С математической точки зрения это означает, что для резонаторной задачи в уравнении (1) СЗ будут являться частоты генерации wj . При таком подходе постоянная распространения β есть характеристика продольной моды лазера, определяемая параметрами резонатора Фабри - Перо. Мы полагаем, что номер генерируемой продольной моды лазера не оказывает существенного влияния на вид поперечных мод. Это означает, что в резонаторной модели мы можем задать одну комплексную постоянную распространения β, которая будет зависеть от длины резонатора L, коэффициентов отражения зеркал по мощности R1 и R2 и внутренних диссипативных (нерезонансных) потерь в резонаторе aint. Выражение для постоянной распространения β, соответствующее М-ой продольной моде, имеет вид:
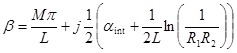 . (2)
. (2)
Кроме приведенных выше соотношений, в самосогласованную модель входит соотношение, связывающее оптическую часть задачи (1) с кинетическими уравнениями (рис.1):
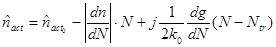 (3)
(3)
где 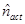 - комплексный показатель преломления активного слоя,
- комплексный показатель преломления активного слоя, 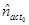 - комплексный показатель преломления активного слоя без накачки,
- комплексный показатель преломления активного слоя без накачки, 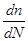 - дифференциальный коэффициент преломления,
- дифференциальный коэффициент преломления, 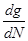 - дифференциальное усиление материала активного слоя,
- дифференциальное усиление материала активного слоя, 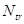 - концентрация нулевого усиления или затухания.
- концентрация нулевого усиления или затухания.
Изложенная методика дает возможность рассчитывать следующие характеристики многослойных лазерных структур: пороговый ток генерации Ith, модовый спектр излучения 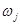 , пространственное распределение интенсивности излучения лазера |yj(x)|2 (в том числе для каждой моды в отдельности), ватт – амперную характеристику
, пространственное распределение интенсивности излучения лазера |yj(x)|2 (в том числе для каждой моды в отдельности), ватт – амперную характеристику 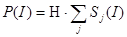 , диаграмму направленности излучения или дальнее поле I(q). Мы не учитываем тепловые, частотные и прочие нелинейные эффекты. Для перевода величины средней плотности фотонов в лазерном резонаторе S в значение выходной мощности лазерного излучения P мы пользуемся следующим соотношением для коэффициента H:
, диаграмму направленности излучения или дальнее поле I(q). Мы не учитываем тепловые, частотные и прочие нелинейные эффекты. Для перевода величины средней плотности фотонов в лазерном резонаторе S в значение выходной мощности лазерного излучения P мы пользуемся следующим соотношением для коэффициента H:
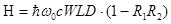 , (4)
, (4)
где 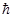 ‑ постоянная Планка, W – ширина области накачки (по оси y),
‑ постоянная Планка, W – ширина области накачки (по оси y), 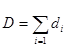 – суммарная эффективная толщина волновода лазерной структуры.
– суммарная эффективная толщина волновода лазерной структуры.
С помощью предложенного алгоритма решения самосогласованной задачи можно косвенно оценивать параметры материалов, из которых сделан лазер. Для этого необходимо сравнение экспериментальных данных с численным расчётом. По алгоритму были проведены расчеты профилей мод и ватт-амперных характеристик для мощных диодных лазеров с вытекающим излучением в оптический резонатор (ДЛ-ВИОР) [4]. Сравнение показало хорошее совпадение расчетных и экспериментальных результатов для ватт – амперной характеристики лазера с шириной полоска 100 мкм и 200 мкм.
Заключение
В данной работе представлен алгоритм решения самосогласованной задачи для многослойных диодных лазеров, с помощью которого возможно рассчитывать следующие характеристики многослойных лазерных структур: пороговый ток генерации, модовый спектр излучения, пространственное распределение интенсивности излучения лазера (в том числе для каждой моды в отдельности), ватт – амперную характеристику, диаграмму направленности излучения или дальнее поле.
ЛИТЕРАТУРА
1. Волноводная оптоэлектроника//Под ред.Т.Тамира, М: Мир, 1991.
2. Buus J. Principles of semiconductor laser modeling. IEE Proceedings, Part J: Optoelectronics, 132 (1), pp. 42-51.1985.
3. Piskorski L., Sarzala R,P Nakvaski, W., Self – consistent model of 650 nm GaInP/AlInP quantum – well vertical – cavity surface – emitting diode lasers. Semiconductor Science and Technology, 22(6), pp. 593 – 600. 2007.
4. В.И. Швейкин, В.А., Геловани. Новые диодные лазеры с вытекающим излучением в оптическом резонаторе. Квантовая электроника, 32, № 8, 2002, стр.683-688.







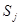 - плотность фотонов в j моде,
- плотность фотонов в j моде, 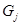 - модовое усиление,
- модовое усиление, 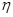 - фактор спонтанного усиления,
- фактор спонтанного усиления, 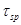 - время спонтанной рекомбинации,
- время спонтанной рекомбинации, 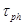 - время жизни фотонов в лазерном резонаторе без накачки e – заряд электрона, d – толщина активного слоя,
- время жизни фотонов в лазерном резонаторе без накачки e – заряд электрона, d – толщина активного слоя, 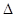 - шаг при итерационном процессе, k – номер итерации.
- шаг при итерационном процессе, k – номер итерации.