При проектировании корпоративных информационных систем (КИС) необходимым условием их успешного применения является научное обоснование принятых решений [1, 2, 3]. Одним из способов научного обоснования является моделирование информационных систем для последующего их анализа и синтеза [4, 5, 6]. В данной работе предлагается использование теории непрерывных марковских цепей [7] для анализа функционирования клиент-серверной архитектуры КИС Восточно-Казахстанского государственного технического университета.
Сформулируем задачу анализа загрузки сервера КИС. Вся обработка информации сосредоточена на сервере системы. Пользователи (к примеру, преподаватели ВУЗа) имеют доступ к серверу со своих автоматизированных рабочих мест (АРМ). Предположим, что в КИС имеется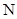 
рабочих мест (пользователей) и сервер, задачей которого является обработка заявок пользователей, т.е. выполнение формируемых на АРМ задач.
Схема соединения АРМ и сервера КИС представлена на рисунке 1.
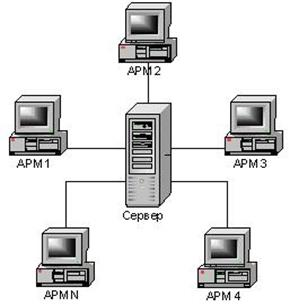
Рис. 1 - Схема соединения АРМ и сервера
Каждый из 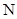пользователей, работающих в КИС, в определенный момент времени может решать свои задачи средствами АРМ или с использованием выделяемого ему серверного ресурса. Многообразие решаемых в КИС задач и их нерегулярность позволяет считать поток обращений пользователя к серверу случайным. Обозначим интенсивности обращений пользователей к серверу КИС через 
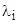, где 
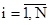. Будем считать, что такой поток является пуассоновским. Последнее позволяет использовать для описания клиент-серверной архитектуры аппарат марковских случайных процессов с дискретным множеством состояний [7].
Введем в рассмотрение вероятность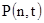 
использования серверного ресурса в момент времени 
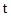ровно 
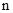пользователями. При этом 
, 
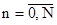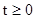. Поставим задачу анализа загрузки сервера КИС, то есть определения функций 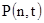, а также наиболее вероятного числа пользователей, использующих серверный ресурс в установившимся режиме работы системы.
Рассмотрим взаимодействие одного АРМ и сервера и определим вероятность нахождения пользователя на АРМ или на сервере в момент времени .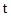
Пользователь в определенный момент времени может находиться в одном из двух состояний: либо он выполняет задачи исключительно на своем АРМ, либо выполняет задачи, используя сервер КИС. Обозначим состояние работы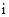 
-го пользователя на АРМ через 
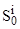, на сервере - через 
.
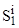Пользователь переходит из состояния в состояние в случайные моменты времени. Если ввести случайные величины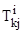 
, определяющие интервалы времени между переходами 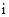-го пользователя из состояния 
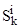в состояние 
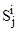, где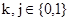 
, а также предположить, что 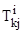подчиняются экспоненциальному закону распределения [7], то интенсивность переходов пользователя из состояния 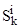в состояние 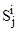можно вычислить как 
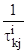, где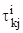 
– математическое ожидание величины .
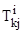При практическом расчете величины 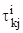могут быть оценены путем сбора статистики с помощью существующих программных средств контроля и анализа КИС таких, как NetWork Monitor для систем семейства Microsoft Windows и др.
Граф связи состояний с интенсивностями переходов представлен на рисунке 2.
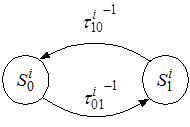
Рис. 2 - Граф связи состояний и интенсивности переходов
Уравнения Колмогорова для данного графа записывается следующим образом [7]:
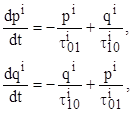(1)
где 
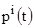и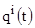 
вероятности пребывания 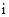-го пользователя в момент времени 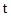на АРМ и на сервере соответственно. Если предположить, что в начальный момент времени все пользователи начинают работать в системе используя только АРМ, то начальные условия для данной системы записываются как:
, 
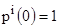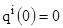. (2)
В каждый момент времени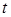 
должно выполняться условие вида:
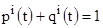. (3)
Учитывая (3), отбросим в (1) второе уравнение, а в первое подставим вместо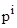 
ее выражение 
:
,
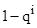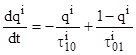или
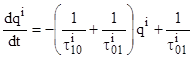. (4)
Решив уравнение (4) при начальных условиях (2) известными методами, получаем:
, .
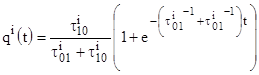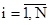Рассмотрим следующее случайное событие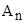 
, состоящее в том, что сервер используют ровно 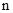пользователей, 
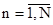. Пусть событие 
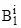означает нахождение 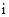-го пользователя на сервере КИС, а 
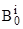- на своем АРМ. Очевидно, что 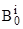и 
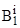составляют полную группу событий. Рассмотрим полную группу событий, составляющих 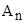, и представим ее в виде:
,
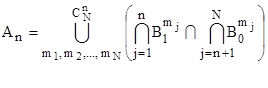где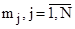 
, - это индексы АРМ (пользователей), то есть 
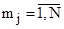и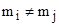 
для всех пар 
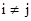. Так как 
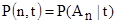и 
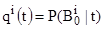, получаем:
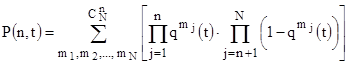. (5)
Для примера приведем вид функций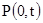 
, 
, 
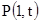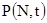. Так как число сочетаний 
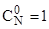, имеется только один вариант выборки индексов в формуле (5) для функции 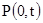, то есть вероятность отсутствия загрузки сервера в момент времени 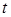имеет вид:
.
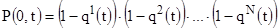Для нахождения функции 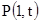, то есть вероятности использования сервера только одним АРМ, необходимо рассмотреть выборку индексов общим числом 
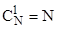. Таким образом, функция 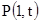представляется как:
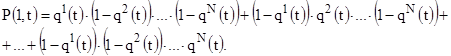
Аналогично можно получить вид функции :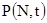
.
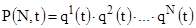Наличие установившего режима в рассматриваемой системе для определенных значени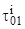й 
и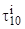 
можно оценить путем анализа функций 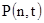. Если для некоторого достаточно малого 
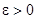будут выполняться условия вида
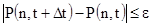для всех 
, 
,
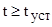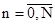то можно говорить о существовании установившегося режима, начиная с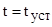 
.
Алгоритм определения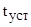 
:
1. Задать достаточно малую величину 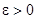и шаг алгоритма 
;
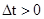2. Определить переменную величину 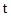с начальным значением 0;
3. Вычислить разности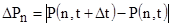 
для каждого ;
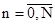4. Если существует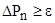 
, то положить 
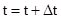и перейти на шаг 3, иначе перейти на шаг 5;
5. Принять за 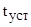величину 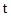и закончить процедуру.
Для нахождения наиболее вероятного числа пользователей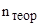 
, использующих серверные ресурсы, необходимо найти функцию 
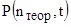, имеющую наибольшие значения для 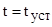, то есть:
.
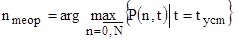Используя предлагаемый подход, можно решить следующие задачи:
1. Оценить для конкретных значени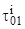й и ,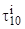 
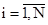, наличие установившегося режима работы системы клиент-серверной архитектуры;
2. Определить момент времени 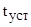, начиная с которого КИС будет функционировать в установившемся режиме;
3. Определить функции вероятности 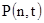числа пользователей, использующих серверные ресурсы, в зависимости от времени;
4. Определить наиболее вероятное число 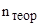пользователей, использующих серверные ресурсы в установившемся режиме.
Сравнивая результаты проведенных теоретических расчетов и опытных данных, можно сделать вывод об адекватности модели для систем архитектуры клиент-сервер.
Литература
1. И. А. Гинатуллин, Задача анализа загрузки серверов корпоративных информационных систем, Исслед. по информ., 10, Отечество, Казань, 2006, 65–72.
2. Волкова В.Н., Денисов А.А. Основы теории систем и системного анализа. – СПб.:Издательство СПбГТУ, 1999.
3. Перегудов Ф.И., Тарасенко Ф.П. Введение в системный анализ. – М.: Высшая школа, 1989.
4. Гинатуллин И.А., Моисеев В.С. Двухуровневая математическая модель корпоративных информационных систем на основе линейных стохастических сетей // Исследования по информатике. Выпуск 7. – Казань: Отечество, 2004. - С. 89-100.
5. Гинатуллин И.А., Моисеев В.С. Зиновьев П.А. Модель для исследования динамики изменений количества пользователей в корпоративных информационных системах // Исследования по информатике. Выпуск 6. – Казань: Отечество, 2003. - С. 111-120.
6. Анфилатов В.С., Емельянов А.А., Кукушкин А.А. Системный анализ в управлении. – М.: Финансы и статистика, 2002.
7. Вентцель Е.С. Исследование операций. – М.: Советское радио, 1972.
