Оценка фоновой составляющей стока валового фосфора с водами контролируемых и неконтролируемых рек бассейна Балтийского моря

Центральной проблемой Балтийского моря в настоящее время стало антропогенное эвтрофирование; одним из важнейших факторов развития этого процесса является биогенная нагрузка с водосборного бассейна моря, которая имеет две составляющие – природную и антропогенную. Чрезвычайно важно в балансе биогенных соединений в море, в миграционных потоках вещества дифференцировать и оценить роль антропогенной составляющей. Основным поставщиком биогенных веществ природного и антропогенного происхождения в Балтийское море является речной сток, что, в общем, является характерным для увлажненной гумидной зоны, в связи с чем очевидна необходимость не только количественной оценки источников эвтрофирующих веществ на территории бассейна, но и дифференцированной фоновой (природной) и антропогенной составляющих биогенного стока рек в замыкающих створах. Однако проблема определения соотношения между величинами природного и антропогенного биогенного стока весьма сложна и до сих пор остается дискуссионной.

В связи с изложенным, цель данного исследования заключалась в оценке выноса фоновой биогенной нагрузки с водами рек бассейна Балтийского моря на примере валового (нефильтрованного) фосфора.

Для оценки фоновых концентраций биогенных элементов (БЭ) в водотоках и фоновых составляющих  биогенного стока нами был разработан метод (именуемый далее метод I), основанный на предложенной Дж. Дэвис и Дж. Цобристом [5] зависимости концентраций растворенного вещества от обратных величин расходов воды в водотоке:

                                                               С_БЭ = А/R + [БЭ]_фон ,                                                     (1)

где С_БЭ – концентрация данной растворенной формы биогенного элемента, [БЭ]_фон – его фоновая концентрация, А – антропогенное поступление в единицу времени, Q – расход реки в единицу времени.

В связи с тем, что уравнение (1) может быть использовано только применительно к растворенным в воде формам биогенных элементов и не распространяется на оценку фоновых концентраций валовых форм, на первом этапе предложенного нами подхода на основе данных о концентрациях общего (растворенного) фосфора Р_общ в водотоке за несколько лет и расходах воды за тот же период проводится определение фоновой концентрации Р_общ. На основании соответствующих фактических данных для р. Нева за период 2001-2004 гг., р. Великая за период 2001-2008 гг., р. Луга за период 2001-2006 гг., р. Желча за период 2002-2007 гг. и р. Нарва за период 2001-2008 гг. были определены фоновые концентрации общего фосфора Р_общ^ФОН  в устьевых створах этих рек (таблица 1).

Таблица 1. Фоновые концентрации общего фосфора в некоторых реках бассейна Балтийского моря

 

На следующем этапе для этих же водотоков были выявлены количественные зависимости между концентрациями общего и валового фосфора, что позволило рассчитать фоновые концентрации валового фосфора. Значения фоновых концентраций валового фосфора были использованы для расчета фоновой составляющей его поступления со стоком рассматриваемых рек в приемные водоемы (таблица 2).

 

Таблица 2. Фоновые концентрации, фоновый сток и модули фонового стока валового фосфора для некоторых рек бассейна Балтийского моря

Река	Приемный водоем	Фоновая концентрация РвалФОН, мкг·дм-3	Фоновый сток Q(Рвал)ФОН, т·год-1	Модуль фонового стока М(Рвал)ФОН,  кг·км-2×год-1	Составляющие суммарного стока, %
					фоновая	антропогенная
Нева	Невская губа	16	1221	4,3	34	66
Великая	Псковское озеро	41	197	7,8	43	57
Нарва	Нарвский залив	25	288	5,1	45	55
Луга	Лужская губа	24	76	5,8	22	78
Желча	Чудское озеро	22	8,9	7,3	52	48

 

Следует отметить, что метод I оценки выноса фоновой биогенной нагрузки применим только для контролируемых рек, для которых имеются данные гидрохимических и гидрологических наблюдений за несколько лет, в связи с чем очевидна необходимость разработки метода, который мог бы быть применен для оценки фонового выноса валового фосфора с территории водосборных бассейнов рек в том числе и в тех случаях, когда имеющихся данных гидрохимических и гидрологических наблюдений недостаточно для применения описанного метода.

Факторы внешней среды, воздействующие на продукционные процессы в водоемах и на суше, тесно связаны с географической зональностью, которую можно рассматривать как фактор, интегрирующий влияние эдафических и климатических условий на продуктивность водных экосистем [1].

Согласно Х. Литу [3], зависимость чистой продукции наземной растительности (ТРР, г·м^-2·год^-1 сухого вещества) от среднегодовой температуры воздуха (Tem, ^оС) и суммы осадков (Pre, мм·год^-1), может быть описана следующими уравнениями:

                                        TPP = 3000 / (1+ exp (1,315 – 0,119·Tem))                                        (2)

                                         TPP = 3000 · (1 – exp (-0,000664·Pre)).                                           (3)

Продукция наземной растительности лимитируется либо температурой, либо осадками. Опираясь на закон Либиха, Х. Лит рекомендует рассчитывать ТРР по уравнениям (2) и (3) и выбирать наименьшую из двух величин.

Соотношение величин фоновой составляющей экспорта фосфора в водоемы и чистой продукции наземной растительности ТРР зависит от скорости разложения наземной растительности, определяемой в значительной мере температурой среды. В среднем для северного полушария  вынос фосфора в водоемы с единицы площади природных ландшафтов (модуль фонового стока М(Р_вал)^ФОН) составляет около 2 % содержания фосфора в первичной продукции, то есть М(Р_вал)^ФОН / ТТР = 0,02 [2]. При этом в направлении от арктических широт к тропическим эффективность выноса фосфора изменяется от 0,3 % до 6 %.

В. В. Бульон [1], исходя из предположения, что скорость разложения наземной растительности как скорость любой химической реакции должна зависеть от температуры согласно уравнению Вант-Гоффа, предложил следующее уравнение зависимости модуля стока фосфора с единицы площади водосборного бассейна от ТРР (ккал·м^-2·год^-1) и температуры:

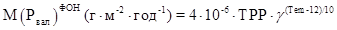                                ,                                  (4)

где сомножитель 4·10^-6 соответствует произведению нескольких эмпирических постоянных: отношения массы органического углерода к его калорийности (0,1 г·ккал^-1), отношения Р : С в растительном материале (0,002) [4], средней доли выноса фосфора для северного полушария в водоемы из наземных экосистем (0,02) [2]; γ – температурный коэффициент скорости реакции, принятый автором равным 2; 12^оС – среднегодовая температура северного полушария.

На основании уравнения (4) и используя приведенные автором [1] зависимости среднегодовой  температуры (5) и количества осадков от географической широты местности (6):

                                                           Tem = 28,2 – 0,41·φ                                                           (5)

                                                           Pre = 2159 – 25,5·φ,                                                           (6)

а также уравнения Х. Лита для зависимости  ТРР от температуры и количества осадков (2) и  (3),   мы   вывели   следующие   уравнения   зависимости   модуля  фонового стока   валового фосфора  М(Р_вал)^ФОН (кг·м^-2·год^-1) от широты местности:

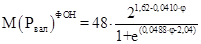                                                                                                    (7)

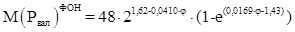                                                                             (8)

Эти уравнения в рассматриваемом нами интервале широт (10-70^о с.ш.) могут быть аппроксимированы уравнениями

                                                   М(Р_вал)^ФОН = 190·exp(-0,0544·φ)                                              (9)

и     

                                                    М(Р_вал)^ФОН = 191·exp(-0,0561·φ)                                           (10)

соответственно.

Уравнения (7) и (9) соответствует лимитированию чистой продукции наземной растительности температурой, а уравнения (8) и (10) – осадками. 

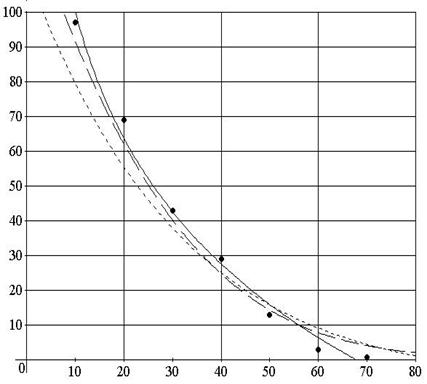
Полученные на основании зависимостей (7-10) значения модуля фонового стока валового фосфора в интервале широт 10^о-70^о с.ш. (рис. 1) отличаются от фактических данных, приведенных  в работе [1], не более чем на 20 %.

М(Рвал)ФОН, кг Р/км2·год
	φ, о с.ш.

Рис. 1.  Зависимость модуля стока валового фосфора с водосборной территории от широты местности

(• фактические данные [1], б)  ——— линия тренда по фактическим данным,  в) – – – –  график зависимости (7),  г) — — — график зависимости (8))

 

На основании фактических данных [1] нами была предложена более точная эмпирическая зависимость между модулем фонового стока валового фосфора с водосборной территории и широтой местности для интервала широт от 10^о с.ш. до 70^о с.ш.:

                                             M(Р_вал)^ФОН = 221 – 52,3×lnj; r² = 0,99                                          (11)

На основании полученной зависимости (11) были выполнены расчеты фонового стока валового фосфора для ряда рек бассейна Балтийского моря в соответствии со следующим алгоритмом (метод II):

1) на схему водосбора реки наносилась координатная сетка посредством калибровки схемы в программе Ozi Explorer [www.oziexplorer.com];

2) проводилось разбиение водосбора в меридиональном направлении на n сегментов с шагом, определяемым исходя из протяженности водосбора с юга на север;

3) в пределах каждого сегмента определялось среднее значение географической широты φ_i, в ^о с.ш.;

4) на основании среднего значения географической широты для каждого сегмента по уравнению (11) вычислялось значение модуля фонового стока валового фосфора с рассматриваемой территории M(P_вал)_i^ФОН;

5) проводилось определение площади территории суши F_i в пределах рассматриваемого сегмента с помощью указанной выше программы;

6) рассчитывалось значение фонового стока валового фосфора Q(P_вал)_i^ФОН с рассматриваемого сегмента водосбора по формуле:

Q(P_вал)_i^ФОН = M(P_вал)_i^ФОН · F_i       

7) суммировались значения фонового стока валового фосфора, рассчитанные для  каждого сегмента, с целью определения суммарного значения фонового стока со всей территории водосбора:

                                                                  _n

Q(P_вал)^ФОН = ∑ Q(P_вал)_i^ФОН      

                                                                                                ^{i   = 1}  

8) на основании полученного результата и общей площади водосбора F  определялось значение модуля фонового стока валового фосфора с рассматриваемого водосбора:

М(P_вал)^ФОН = Q(P_вал)^ФОН/F      

Результаты расчетов для рек Нева, Нарва, Луга, Желча и Великая, полученные в рамках метода II, были сопоставлены с результатами, полученными методом I (таблица 3); расхождение между величинами фонового поступления валового фосфора, рассчитанными разными методами, варьирует от 5 % (р. Желча) до 34 % (р. Нарва), что по нашему мнению вполне допустимо, учитывая точность подобного рода оценок.

 

Таблица 3. Поступление валового фосфора со стоком некоторых рек бассейна Балтийского моря

Река	Метод I		Метод II		Δ Q, %
	М(Рвал)ФОН, кг·км-2×год-1	Q(Рвал)ФОН, т·год-1	М(Рвал)ФОН, кг·км-2×год-1	Q(Рвал)ФОН,  т·год-1
Нева	4,3	1221	4,9	1382	12
Луга	5,8	76	6,8	90	16
Нарва	5,1	288	7,8	439	34
Желча	7,3	8,9	7,7	9,4	5
Великая	7,8	197	9,3	234	16

 

Метод II дает в целом более высокие значения фонового поступления валового фосфора, чем метод I; по-видимому, это объясняется тем, что метод II не позволяет учитывать удержание фосфора  в гидрографической сети, в то время как при оценке фонового поступления валового фосфора по  методу I используются данные гидрохимических измерений в замыкающих створах рек, реально учитывающие удержание фосфора поверхностными водами суши.

Также нами было показано, что для расчетов величин фонового стока валового фосфора с водосборных территорий рек с небольшими водосборами в первом приближении могут быть использованы значения географической широты в средней точке водосбора (φ_ср), поскольку это приводит к относительной погрешности немногим более 1 % (в случае протяженности водосбора с юга на север в пределах 2^о с.ш.).

Изложенное выше позволяет сделать вывод о допустимости применения предложенного метода для оценки фонового стока валового фосфора с водосборов рек, в том числе частично контролируемых и неконтролируемых.

 

Литература

1. Бульон В. В. Эвтрофирование и деэвтрофирование озер как реакция на изменения фосфорной нагрузки с водосборной площади // Теория и практика восстановления внутренних водоемов / Под ред. Румянцева В. А., Кондратьева С. А.  – СПб: Лема, 2007. С. 44-54.  

2. Коплан-Дикс И. С., Назаров Г. В., Кузнецов В. К. Роль минеральных удобрений в эвтрофировании вод суши. – Л.: Наука, 1985. – 182 с.

3. Лит Х. Моделирование первичной продуктивности Земного шара // Экология, 1974. № 2. С. 13-23.

4. Эволюция круговорота фосфора и эвтрофирование природных вод / Под ред.  Кондратьева К. Я., Коплан-Дикса И. С. – Л.: Наука, 1988. 204 с.

5. Davis J. S., Zobrist J. The interrelationships among chemical parameters in rivers – Analysing the effect of natural and anthropogenic sources // Progress in water technology. 1978. Vol. 10. P. 65-78.