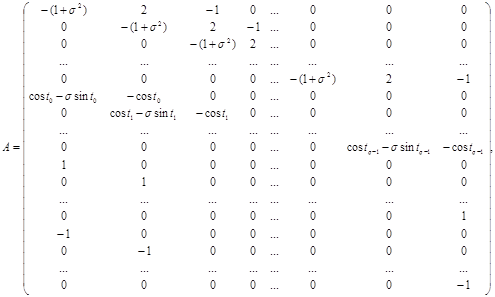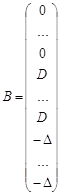1. Введение.
Разнообразные задачи геометрии на экстремум площади и объема при заданных ограничениях на периметр решались известными математиками с глубокой древности. Классическая изопериметрическая задача состоит в определении кривой заданной длины, ограничивающей максимальную площадь. К таким задачам относятся задача Архимеда, в которой требуется среди шаровых сегментов, имеющих заданную площадь поверхности, найти сегмент максимального объема; задача Зенодора, в которой среди n-угольников, имеющих заданный периметр, необходимо найти n-угольник наибольшей площади; задача о геодезической кривой наименьшей длины, лежащей на заданной поверхности, и многие другие. Решение изопериметрических экстремальных задач важно не только с теоретической, но и практической точки зрения. В частности, такие задачи возникают при раскрое и упаковке промышленных материалов с целью снижения количества отходов, при размещении грузов на палубах судов, в отсеках самолетов и других. Целью данной работы является разработка и исследование численных методов и алгоритмов оптимизации для решения пространственных выпуклых изопериметрических задач. В работе рассматривается задача о построении выпуклой пространственной фигуры максимальной площади поверхности при заданных ограничениях на ширину фигуры.
В настоящее время разработано большое количество численных методов решения задач оптимального управления и нелинейного программирования и работа по их созданию и совершенствованию продолжается [7]-[11]. Из широко известных численных методов можно выделить два основных типа: прямые и непрямые. В прямых методах поиск решения заключается в нахождении предельных точек минимизируемых (максимизируемых) последовательностей в пространстве исходных переменных. Среди них - модификации метода проекции градиента, метод возможных направлений и другие. В методах второго типа решение задачи сводится к задачам безусловной минимизации. Данный переход, в частности, происходит вследствие изменения методов внешней и внутренней (барьерной) штрафной функции, метода модифицированной функции Лагранжа, метода с оценкой критерия и других. Вычислительные подходы к решению задач нелинейного программирования и поиска оптимального управления получили широкое освещение и систематизацию в работах Ю.Г.Евтушенко [8]-[10].
1. Формализация пространственных изопериметрических задач.
В работе формализация пространственных изопериметрических задач осуществляется с помощью опорной функции выпуклого множества.
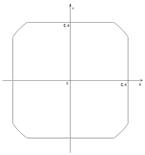
Плоскость 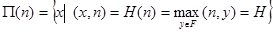 назовем опорной плоскостью выпуклого множества
назовем опорной плоскостью выпуклого множества  в направлении n, функцию
в направлении n, функцию 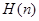 - опорной функцией фигуры
- опорной функцией фигуры 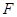 в направлении n.
в направлении n.
Введем сферические координаты в трехмерном евклидовом пространстве, тогда 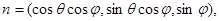
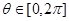 ,
, 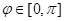 .
.
Положим 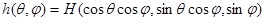 ,
, 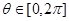 ,
, 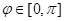 , и назовем эту функцию опорной функцией фигуры
, и назовем эту функцию опорной функцией фигуры 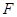 в соответствующем направлении.
в соответствующем направлении.
Аналогично при введении полярных координат в 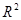 вводится понятие опорной функции плоской фигуры в
вводится понятие опорной функции плоской фигуры в 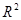 :
: 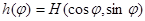 ,
, 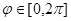 .
.
Если опорная плоскость имеет только одну общую точку с множеством, то эта опорная плоскость является регулярной. Если все опорные плоскости множества 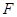 регулярны, то назовем такое множество регулярным множеством или овалом, а его опорную функцию – регулярной опорной функцией множества
регулярны, то назовем такое множество регулярным множеством или овалом, а его опорную функцию – регулярной опорной функцией множества 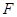 .
.
Определим ширину выпуклой пространственной фигуры 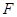 в направлении n:
в направлении n:
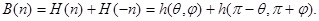
Диаметром выпуклой фигуры 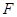 назовем
назовем
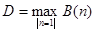 .
.
Толщина выпуклой фигуры 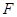 определяется равенством
определяется равенством
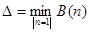 .
.
|
|
|
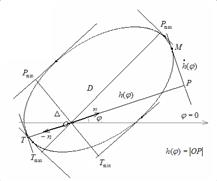
Рис.1 Опорная функция выпуклой фигуры |
Теорема [15]: Опорная функция выпуклой замкнутой регулярной фигуры в 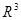 почти всюду на множестве
почти всюду на множестве 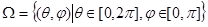 удовлетворяет неравенству:
удовлетворяет неравенству:
|
|
(1) |
Площадь поверхности выпуклой пространственной фигуры определяется выражением:
|
|
(2) |
Опорная функция рассматриваемых фигур удовлетворяет граничным условиям:
|
|
(3) |
2. Постановка задачи.
Требуется найти выпуклую фигуру вращения, имеющую максимальную площадь поверхности при заданных ограничениях на ее ширину. Поиск фигур осуществляется в классе выпуклых фигур вращения с опорной функцией 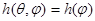 . Обозначим через
. Обозначим через 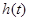 значение опорной функции фигуры в направлении t.
значение опорной функции фигуры в направлении t.
Для фигуры вращения формула (2) имеет вид:
|
|
(4) |
ограничения на ширину:
|
|
(5) |
условия выпуклости:
|
|
(6) |
В заданных направлениях 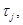
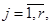 накладываются дополнительные ограничения на ширину:
накладываются дополнительные ограничения на ширину:
|
|
(7) |
где параметры 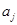 ,
, 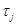 удовлетворяют условиям:
удовлетворяют условиям:
|
|
(8) |
Не ограничивая общности рассмотрения, положим 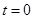 в направлении толщины искомой фигуры:
в направлении толщины искомой фигуры:
|
|
(9) |
Пусть далее 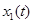 - ширина фигуры в направлении t:
- ширина фигуры в направлении t: 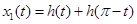 ,
, 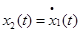 ,
, 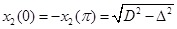 . Задача формализуется как задача оптимального управления, где роль функции управления играет радиус кривизны
. Задача формализуется как задача оптимального управления, где роль функции управления играет радиус кривизны 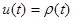 ,
, 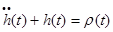 [4]. Динамические ограничения и ограничение на управление следуют из условия выпуклости фигуры.
[4]. Динамические ограничения и ограничение на управление следуют из условия выпуклости фигуры.
Задача (4)-(9) формализуется как задача оптимального управления с фазовыми и промежуточными ограничениями:
|
|
(10) |
|
при динамических ограничениях: |
|
|
|
(11) |
|
ограничениях на управление: |
|
|
|
(12) |
|
фазовых ограничениях: |
|
|
|
(13) |
|
промежуточных |
|
|
|
(14) |
|
и граничных условиях: |
|
|
|
(15) |
|
|
(16) |
3. Решение задачи нелинейного программирования.
Применим к решению рассматриваемой задачи методы математического программирования. Заметим, что система (11),(12) может быть представлена в виде:
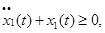
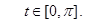
Аппроксимируя производные по формуле Эйлера, получим следующие неравенства в узлах разбиения:
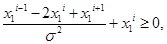
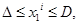
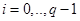 ,
,
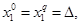
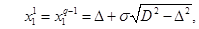
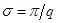 .
.
Промежуточные ограничения описываются соотношениями:
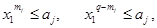
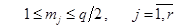 .
.
Задача нелинейного программирования состоит в минимизации функции
|
|
(17) |
при линейных ограничениях:
|
|
(18) |
|
|
(19) |
|
|
(20) |
где 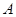 - матрица размерности
- матрица размерности 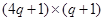 ,
, 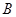 - вектор размерности
- вектор размерности 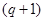 ,
,
|
|
|
(21) |
В этом случае неизвестным является вектор значений траектории 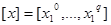 . Применяя метод проекции градиента, проектируем антиградиент минимизируемой функции
. Применяя метод проекции градиента, проектируем антиградиент минимизируемой функции 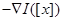 так, что направлением спуска становится вектор
так, что направлением спуска становится вектор 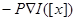 , где
, где 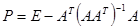 - соответствующая матрица проектирования [14],
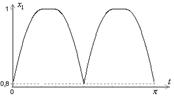
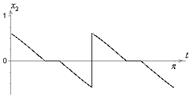
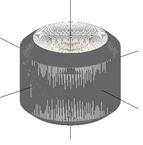
- соответствующая матрица проектирования [14], 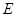 - единичная матрица. Результаты решения задачи приведены на рис.2-6, табл.1.
- единичная матрица. Результаты решения задачи приведены на рис.2-6, табл.1.
|
|
|
|
|
|
Рис.2. График функции ширины |
Рис.3. График |
Рис.4. График функции радиуса кривизны |
|
|
|
|
|
|
|
Рис.5. Вид сечения оптимальной фигуры |
Рис.6. Вид оптимальной фигуры |
Таблица 1. |
|
Таким образом, использование дифференциальных связей в качестве ограничений и аппроксимация непрерывной задачи задачей нелинейного программирования оказывается эффективным подходом при разработке численных методов решения экстремальных геометрических задач. Методы нелинейного программирования демонстрируют высокую производительность при построении оптимального решения рассматриваемого класса задач в широком диапазоне изменения параметров.
Литература
1. Андреева Е.А. Оптимальное управление динамическими системами. Тверь, 1999.
2. Андреева Е.А., Цветкова Е.Г., Савичева Ю.А. Решение экстремальных задач геометрии двойственным методом: Учеб. пособие. - Тверь: ТвГУ, 2007.- 180 с.
3. Андреева Е.А., Надь Е. Двойственность в теории экстремальных задач. Международная школа по оптимальному управлению. Учебное пособие., Калинин, 1985.
4. Бляшке В. Круг и шар.- М.: Наука, 1951.
5. Болтянский В.Г., Яглом И.М. Выпуклые фигуры. М.: Наука, 1951.
6. Боннезен Т., Фенхель В. Теория выпуклых тел.- Берлин, 1934.
7. Васильев Ф.П. Лекции по методам экстремальных задач. М.:Московский университет, 1974.
8. Евтушенко Ю.Г. Методы решения экстремальных задач и их применение в системах оптимизации. М.: Наука, 1982.
9. Евтушенко Ю.Г., Мазурик В.П. Программное обеспечение систем оптимизации.- М.: Знание, 1989. 48 с.
10. Евтушенко Ю.Г., Жадан В.Г. Барьерно-проективные методы решения задач нелинейного программирования //ЖВМиМФ, 2002, Т.34.
11. Дубовицкий А.Я., Милютин А.А. Задачи на экстремум при наличии ограничений. М., ЖВМиМФ, 1965, №3.
12. Красноженов Г.Г. Применение численных методов к решению экстремальных задач геометрии. Диссертация канд. ф.м. наук. Тверь, ТвГУ, 2001.
13. Мухачева Э.А. Рациональный раскрой промышленных материалов, М., Машиностроение, 1984.
14. Трифонов А.Г. Постановка задачи оптимизации и численные методы ее решения, М., Дело, 2002.
15. Цветкова Е.Г. Построение оптимальных пространственных фигур методами нелинейного программирования. Диссертация канд. ф.м. наук. Тверь, ТвГУ, 2009.







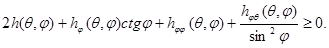
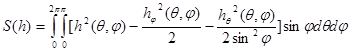
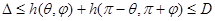
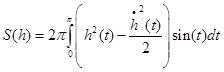
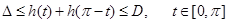 ,
,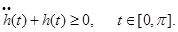
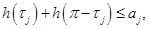
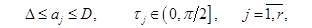
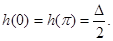
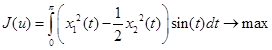 ,
,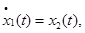
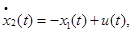
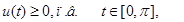
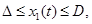
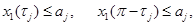
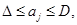
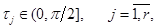
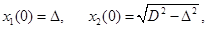
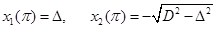 .
.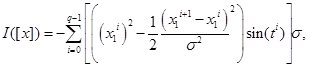
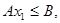
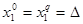 ,
, 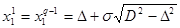 .
.