Рассмотрение вопросов разработки цифрового понижающего преобразователя под управлением нелинейного регулятора, синтезированного методом аналитического конструирования агрегированных регуляторов (АКАР).
Ключевые слова: метод аналитического конструирования агрегированных регуляторов(АКАР), нелинейный регулятор, цифровой понижающий преобразователь.
Никто из нас не задумывается насколько нелинейный вокруг нас окружающий мир и процессы, которые происходят в нем. Известная фраза Гераклита: «На входящих в одну и ту же самую реку набегают все новые и новые воды…», прозвучавшая около двух с половиной тысячелетий назад, указывает на переменчивость окружающего мира. Современная теория динамических систем является наследницей традиций классического естествознания, в ее основе лежит опыт теоретических и экспериментальных исследований нескольких столетий, среди ее основателей — великие ученые прошлого — Ньютон, Лагранж, Лаплас, Гамильтон, Якоби, Эйлер, Пуанкаре и многие другие. Эпоха научно-технического прогресса поставила перед динамикой ряд новых задач, не вписывающихся в рамки классических подходов и существующей научной парадигмы. Назрело концептуальное перевооружение динамики, предполагающее введение новых понятий и разработку принципиально новых математических методов.
Такая «новая» динамика начала формироваться в прошлом столетии. Ее отличительной особенностью стало изучение так называемых «нелинейных эффектов», возникающих при использовании нелинейных уравнений движения. Именно по этой причине «новую» динамику принято называть нелинейной динамикой. И именно эту «новую» динамику многие специалисты не спешат внедрять в разрабатываемые системы управления. Применяя методы линеаризации нелинейных динамических систем с последующим управлением с помощью линейных регуляторов. На это есть ряд причин.
Публикации, научные книги практического применения нелинейных регулятор для различных систем практически отсутствуют. В большинстве научно-исследовательских работах можно найти только математическое моделирование расчетов нелинейного регулятора. Естественно это отталкивает разработчиков и замедляет процесс вытеснения традиционных линейных регуляторов. Благодаря таким программным продуктам как «Matlab», сложность проектирования ПИД-регулятора для автоматических систем управления минимизируется. На стадии разработки системы управления объектом с помощью «Matlab» мы можем выявить ошибки. Встроенный в «Matlab» генератор кода для ПЛИС и ряда микроконтроллеров ведущих производителей таких как «TexasInstrument», «STMicroelectronics», позволяет избавить разработчика от рутинной работы переноса программного кода. Применение блоков нечеткого регулятора, автоматической настройки ПИД-регулятора, позволяет разработчикам охватить все области автоматического управление.
Применение линейного регулятора в нелинейных системах приводит к ограничению области устойчивости и не возможности подавить внешние неопределенные возмущающие воздействия. В целях расширения области устойчивости применяются ПИД-регуляторы с автоподстройкой коэффициентов. В различных режимах работы объекта может происходит переключением между ПИ, ПД и ПИД регулятором. Расширение области устойчивости зависит полностью от разработчика. Если отклонение параметров системы от расчетных будет увеличиваться, или система перейдет в непредусмотренный режим работы, линейный регулятор неизбежно дестабилизирует систему, так как разработчик это не предусмотрел. Прорывом в данных проблемах стало применение нечеткого регулятора. Но нечеткая логика программируется разработчиком и по-прежнему ей неизвестна структура управляемой системы. Отличительная характеристика нелинейного регулятора заключается в наличии всех параметров управляемой системы. Это позволяет ему несмотря на изменения состояния системы вывести управляемый объект к заданным параметрам.
В серии статей, ориентированных на инженеров-разработчиков, будет показан синтез нелинейного регулятора методом аналитического конструирования агрегированных регуляторов (АКАР) для импульсного понижающего DC-DC преобразователя напряжения с последующей его реализацией на микроконтроллере. Будет проведен сравнительный анализ достоинств и недостатков синтеза и переходных процессов в сравнении с ПИД-регулятором.
Метод «АКАР».
Метод аналитического конструирования агрегированных регуляторов (АКАР) базируется на принципе «расширения — сжатия» фазового пространства. Целью данного регулятора заключается в переходе от непредсказуемого поведения системы по алгоритму диссипативной структуры к направленному движению вдоль желаемых инвариантных многообразий — аттракторов, к которым подстраиваются все другие переменные динамической системы. При таком подходе цель — аттрактор — определяет сущность процесса, а его истинное понимание состоит в самоуправлении и направленной самоорганизации в соответствии с поставленной целью. На языке теории динамических систем это означает перевод соответствующей системы в определенное конечное состояние независимо от ее прежнего состояния.
Из выше сказанного следует, что полученное управляющее воздействие в результате синтеза регулятора, должно при любых изменениях режимов работы стабилизировать выходное напряжение понижающего преобразователя. У инженеров сразу же возникает справедливый вопрос, как быть с режимом прерывистых токов. Данный режим работы является проблемой, над решением которой работают ведущие производители ШИМ-контроллеров. Уменьшение тока потребления холостого хода особенно актуально в аккумуляторных системах. Не менее важен переходной процесс от минимальной токовой нагрузки к максимальной и обратно. Все эти проблемы будут подробно описаны.
Рассмотрим синтез регулятора понижающего преобразователя в режиме непрерывных токов и постоянной частоты работы силового ключа.
Синтез регулятора методом АКАР нельзя провести без динамической системы уравнений. Это вводит определенные трудности, чем сложнее управляемый объект, тем больше дифференциальных уравнений необходимо составить. Математическую модель понижающего преобразователя в соответствии с законами Кирхгофа можно представить:
 (1)
(1)
Система (1) учитывает эквивалентное последовательное сопротивление (ЭПС) выходного конденсатора «Rс», сопротивление силового ключа «Ron»«, если применяется полевой транзистор, частоту работу ШИМ-генератора. То есть система (1) составлена под конкретное схемное решение. В качестве силового ключа выступает полевой транзистор, задана частота работы и т. д. Представим ситуацию, где применение в электрической схеме биполярного транзистора является более оправданным, чем установка полевого транзистора. Необходимо составлять «новую» математическую модель системы. Синтезировать закон управления для всех схемных решений, весьма затруднительно. Решением должно стать единое управляющее воздействие, позволяющее менять силовые ключи, драйверы силовых ключей.
Произведем упрощение математической модели. Частота ШИМ-сигнала постоянна, то есть во время работы преобразователя она константа. Транзистор представим идеальным ключом, это позволит применять как полевой, так и биполярный транзистор. И в заключении упрощения не будем учитывать ЭПС конденсатора.
Упрощение математической модели усложняет задачу для «АКАР», регулятор не имеет всех данных о управляемой системе это противоречит основным принципам синтеза методом АКАР согласно [1]. После упрощения электрической схемы (рисунок 1) понижающего преобразователя можно записать усредненную математическая модель в форме Коши, полученную в работе [2]:
 (2)
(2)
Где: Ein — входное напряжение; u — рабочий цикл (управляющее воздействие); iL — ток индуктивности; r — сопротивление обмотки индуктивности; Uout — выходное напряжение; C — выходной конденсатор; iout — ток нагрузки.
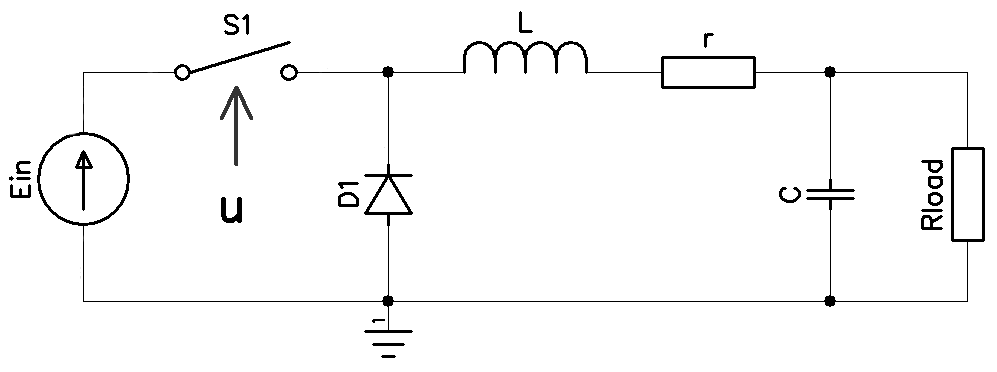
Рис. 1.
Поясним цель упрощения системы дифференциальных уравнений. В результате в системе (2) остаются элементы, которые независимо от схемного решения, принятого разработчиком, всегда будут в понижающем преобразователе. Данные элементы можно назвать основными, ввиду их влияния на динамику и принцип работы преобразователя. С точки зрения синтеза методом АКАР это не правильное решение, так как чем полнее записана модель, тем точнее управляющее воздействие. С инженерной точки зрения нами будет получено управляющее воздействие, позволяющее менять электрическую схему под различные задачи не производя синтез регулятора заново.
Синтез методом АКАР осуществляется путем ввода желаемой переменной, к значению которой переводится наша система. Желаемая переменная это заданное разработчиком напряжение на выходе «Uc». Метод АКАР должен перевести нашу систему, импульсного понижающего преобразователя, из любого состояния к аттрактору «Uc = Uout» по средствам расчета управляющего воздействия. Ввод желаемой переменной осуществляется различными способами и методами. Мы применим метод интегральной адаптации. Для этого расширим исходную динамическую систему (1) дифференциальным уравнением:
 (3)
(3)
Принцип работы метода интегральной адаптации заключается в нахождение величины ошибки между заданным и выходным напряжением. Изменяя значения переменной «η», меняется динамика расчета величины ошибки. Так как выходное напряжение определяется во втором уравнении системы (3), необходимо вычесть «z» от всей правой части уравнения. Это увеличит рассогласование системы, пока ошибка «Uc-Uout» не станет равной нулю. Можно заметить некоторую идентичность метода интегральной адаптации с принципом работы интегральной составляющей ПИД-регулятора.
Переходим к синтезу управляющего воздействия, так как нам необходимо стабилизировать ![]() находящееся во втором уравнение, водим первую макропеременную:
находящееся во втором уравнение, водим первую макропеременную:
![]() (4)
(4)
Где φ(Uout,z) — внутреннее управление
Применяя основное функциональное уравнение(ОФУ):
![]() (5)
(5)
Подставляя (4) в (5) находим внутреннее управление:
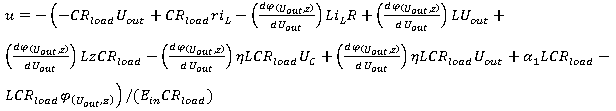 (6)
(6)
В результате попадания системы в окрестность многообразия Ѱ1=0 (4) в системе происходит динамическая декомпозиция и поведение системы будет описываться системой дифференциальных уравнений второго порядка:
 (7)
(7)
Вводим вторую макропеременную для системы (7):
![]() (8)
(8)
Применяем ОФУ для нахождения φ(Uout,z):
![]() (9)
(9)
Полученный результат (9) подставляем в (6):
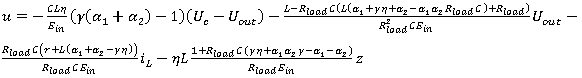 (10)
(10)
Синтезированное управляющее воздействие обеспечить перевод динамической системы (1) из произвольного состояния вначале в окрестность многообразия Ѱ1=0, а затем в состояние, определяемое требуемым значением выходного напряжения «Uc=Uout». Коэффициенты «α1,α2,γ,η» настраиваются таким образом, чтобы получить желаемый переходной процесс. Изменяя значение коэффициентов регулируется время выхода на заданное напряжение, выброс напряжения при изменении нагрузки, величина перерегулирования.
Моделирование.
Проведем моделирование динамической системы (1) в «Matlabm-file» изменяя ступенчато ток нагрузки, рисунок 2. Значения элементов схемы рассчитаны в работе [3]:


Рис. 2. Графики изменения выходного напряжения в зависимости от тока нагрузки
Анализируя графики рисунка 2 можно отметить преимущество метода «АКАР» в сравнении с ПИД-регулятором это отсутствие колебаний в переходном процессе. Недостатком «АКАР» является его реализации в «железе». Формулу (10) собрать на радиоэлементах весьма проблемно, еще сложнее провести настройку коэффициентов «α1,α2,γ,η». Решение одно, применение цифрового «ШИМ-контроллера» на основе микроконтроллера, процессора или ПЛИС. Таким образом метод «АКАР» в области преобразователей напряжения может применяться только в цифровом виде.
Проведем моделирование в «MatlabSimulink» электрической схемы понижающего преобразователя с управляющим воздействием полученного из усредненной математической модели (1). Примем следующие параметры радиоэлементов, которые не учитывались в системе дифференциальных уравнений (1), рисунок 3:
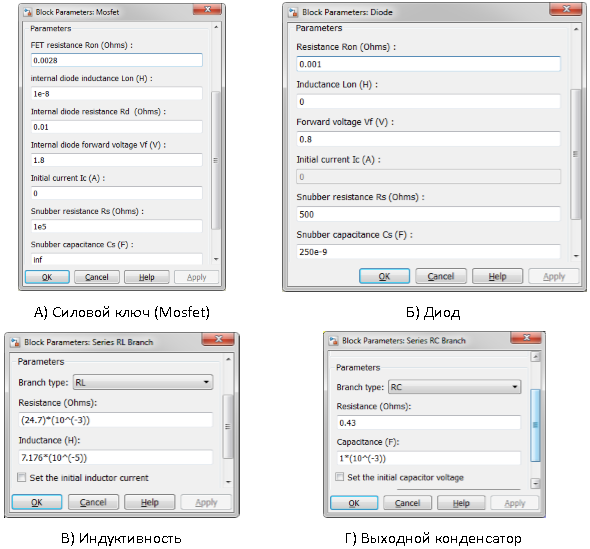
Рис. 3. Параметры радиоэлементов
Электрическая схема преобразователя в «MatlabSimulink» представлена на рисунке 4. Блок «PWM» формирует ШИМ-сигнал с частотой 100кГц. Расчет управляющего воздействия, интегральной адаптации «z» производится в блоке «AKAPcontrolaction» («MATLABFunction»). Нагрузка «Load» константа 0,5. Входное напряжение «DCVoltageSource» константа +30В. Выходное напряжение «Uс» константа +5В. Коэффициенты управляющего воздействия «α1=500, α2=1000, γ=1000, η=5»
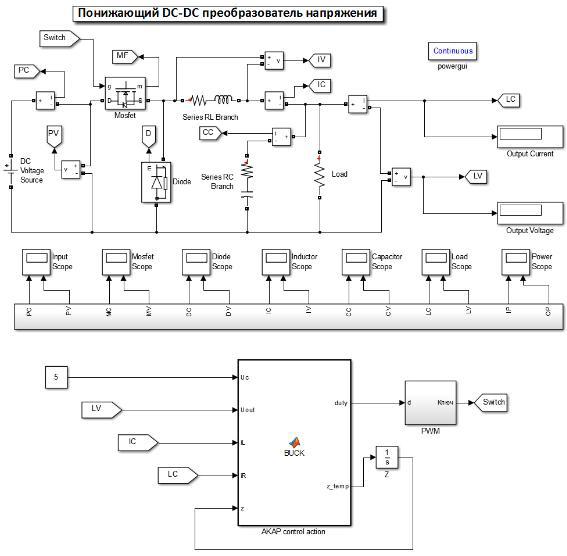
Рис. 4. Электрическая схема понижающего преобразователя под управлением «АКАР» в «MatlabSimulink»
Результаты моделирования представлены на рисунке 5. Осциллограммы выходного напряжения и тока нагрузки позволяют сделать вывод, что «АКАР» полностью справился с поставленной задачей, не имея данных о применяемом типе силового ключа, драйвера силового ключа и ЭПС конденсатора.

Рис. 5. Осциллограммы тока нагрузки и выходногонапряжения
Заключение.
В первой части статьи «Цифровой импульсный понижающий преобразователь напряжения под управлением «АКАР» мы рассмотрели синтез регулятора понижающего DC-DC преобразователя методом аналитического конструирования агрегированных регуляторов. Доказана целесообразность применения упрощенной математической модели при синтезе регулятора. Это позволило получить управляющее воздействие относительно постоянных радиоэлементов, применяемых при разработке понижающего преобразователя. Таким образом допускаются замены в электрической схеме, без составления «новой» математической модели, следующих элементов:
силовой ключ (биполярный, полевой N/P-канальный транзистор),
драйвер силового ключа,
диод,
входной, выходной конденсаторы.
Разработчику необходимо настроить коэффициенты «α1, α2, γ, η» в соответствие с током нагрузки, выходным напряжением и желаемым переходным процессом.
Моделирование математической модели показало отсутствие колебаний в переходном процессе, в отличии от ПИД-регулятора.
В следующей части подробно рассмотрим переходные процессы при изменении нагрузки и как ими управлять.
Литература:
- А. А. Колесников «Современная прикладная теория управления» 1, 2, 3 том, 2000 г.
- Межаков О. Г. Математическая модель понижающего преобразователя напряжения // Молодой ученый. — Март 2015 — с. 171–176.
- Межаков О. Г., Скляров А. А. ПИД-регулятор понижающего преобразователя напряжения // Молодой ученый. — Май 2015 — с. 257–260.
- Marian K. Kazimierczuk «Pulse-width modulated dc–dc power converters», 2008 г.
- R. W. Erickson «Fundamentals of Power Electronics», 1997 г.
- В. С. Щербаков, А. А. Руппель, И. В.Лазута, С. А.Милюшенко «Автоматические системы управления в среде Matlab-Simulink», 2010 г.
- И. В. Черных. «Simulink Инструмент моделирования динамических систем».







