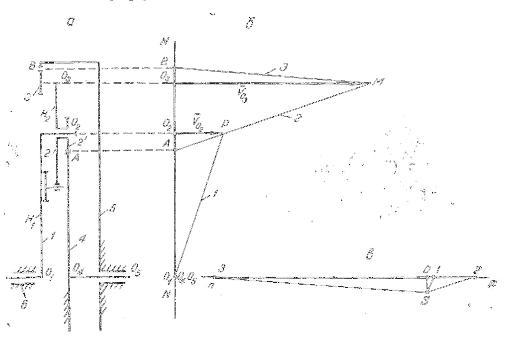
В настоящей работе рассмотрим структуру и кинематику планетарного механизма со ступенчатым сателлитом (рисунок, а), состоящего из следующих подвижных и неподвижных звеньев, а также кинематических пар (1): 1-водило, 2-сателлит-водило, 3-сателлит, 4,5-неподвижные центральные колеса, 6-стойка, три вращательные пары пятого класса
; 
; 
две кинематические пары четвертого класса
; 
.
Поскольку все звенья движутся в параллелных плоскостях, механизм считается плоским. Степень его подвижности определяется по известной структурной формуле П. Л. Чебышева (2).
(1)
Где n=3 — число подвижных звеньев; 
или 
— число кинематических пар пятого и четвертого классов.
Подставив значения n, p5 и p4 в структурнуюформулу (1), получим W=1. Это значит, что для определения движения звеньев данного планетарного механизма необходимо задать движение одного звена, например, водила H1, являющего ведущим.
В работе (3) доказано, что структура планетарных механизмов с произвольной степенью подвижности может быть исследована по формуле
. (2)
где 
, 
, 
— количество самостоятельных водил, сателлитов, неподвижных звеньев, находящихся в зацеплении. Применительно к представленной кинематической схеме будем идеть kc.в=2, kc.с=1, kн.з=2, тогда 
.
Рассмотрим кинематику планетарного механизма со ступенчатым сателлитом (схему определения линейных и угловых скоростей характерных точек механизма см.на рисунке, б).
Угловые скорости 
и 
(см. рисунок, а) можно найти аналитически с учетом векторных свойств радиусов сопряжения (4):
; (3)
где 
Тогда угловая скорость 
с учетом 
будет иметь вид
(4)
Скорости точки 
определимиз подобия треугольников Δ
Δ
(см.рисунок, б):
, отсюда 
(5)
Подставив в (5) соответствующие значения, получим скорость точки
(6)
Тогда угловая скорость 
с учетом 
вычислится по формуле
=
(7)
Подставив значение (4) в (7), найдем общую формулу для определения угловой скорости сателлита
Литература:
- Усманходжаев Х. Х. Теория механизмов и машин. На узб.яз. — Ташкент: Фан УзССР, 1981.
- Артоболевский И. И. Теория механизмов. — М.: Наука, 1965.
- Файзиев И. Х. Структурный анализ и синтез планетарных механизмов с произвольной степенью подвижности. Вопросы кибернетики и вычислительной математики. — Ташкент: Фан, 1968. № 20 — С.96–103.
