В работе рассмотрен вопрос представления алгоритма в матрично-предикатном виде в модульной и в матрично-предикатной форме. Показано, что при большой разреженности получаемы матриц их можно заменить на таблицы, то есть задавать алгоритм в таблично-предикатной форме.
Ключевые слова: алгоритм, предикат, матрица, таблица, граф.
Классическое представление алгоритма — словесное или в виде блок-схем — несмотря на то, что отличается легкостью восприятия и наглядностью, имеет существенный для определенного класса задач недостаток — низкую формализацию. Особенно важно это в случаях составления алгоритмов для параллельных процессов, работы сложных многокомпонентных и многокритериальных систем. В этих случаях необходимо снизить уровень эвристики и повысить уровень формализма. Следовательно, желательно представить алгоритм в виде упорядоченной структуры. Таковой и являемся матричная форма, в структуру которой входят элементы теории предикатов, способ задания которой и рассматривается ниже.
В графическом виде алгоритм изображается последовательностью связанных между собой функциональных блоков, каждый из которых соответствует выполнению одного или нескольких действий. Такое представление называется схемой алгоритма, или блок-схемой, или граф-схемой алгоритма (ГСА).
В настоящее время алгоритмы рассматриваются как последовательностные структуры, то есть выполнение операций осуществляется последовательно.
Рассмотрим произвольную ГСА (рис. 1).
Здесь:
![]() – вершины, определяющие выполнение отдельных операций, будем называть функциональными блоками или блоками действия;
– вершины, определяющие выполнение отдельных операций, будем называть функциональными блоками или блоками действия;
![]() – вершины, определяющие логику (порядок) выполнения алгоритма, будем называть предикативными или логическими блоками.
– вершины, определяющие логику (порядок) выполнения алгоритма, будем называть предикативными или логическими блоками.
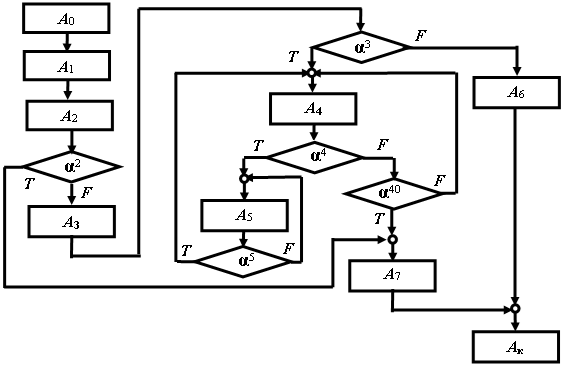
Рис. 1. Граф-схема алгоритма
Задание алгоритма в виде ГСА имеет ряд недостатков:
переход от выполнения одной операции к выполнению другой в некоторых случаях ничем не обозначен, например, вершины А0 — А1 — А2, здесь подразумевается, что после выполнения операции А1 следует переход к выполнению операции А2, хотя такой переход ничем не фиксируется;
условия, определяющие порядок выполнения алгоритма, часто задаются несколькими логическими функциями, например α4–α40, что усложняет рассмотрение алгоритма.
Первый из этих недостатков устраняется путём объединения двух или нескольких операторов действия в один, например, вершины А0 — А1 — А2, заменяют на оператор А012, или окончание каждого из функциональных операторов действия фиксируется окончанием зоны их действия.
Второй из этих недостатков устраняется путём объединения нескольких логических функций одной известными приёмами алгебры логики.
В результате проведения таких операций, которые будем называть в дальнейшем операциями доопределения, приходим к начертанию алгоритма в виде модульных блоков (рис. 2).
Пунктиром выделены модули алгоритма, а на рисунке (рис. 3) приведено изображение алгоритма в модульном исполнении, которое представляет собой граф Бержа
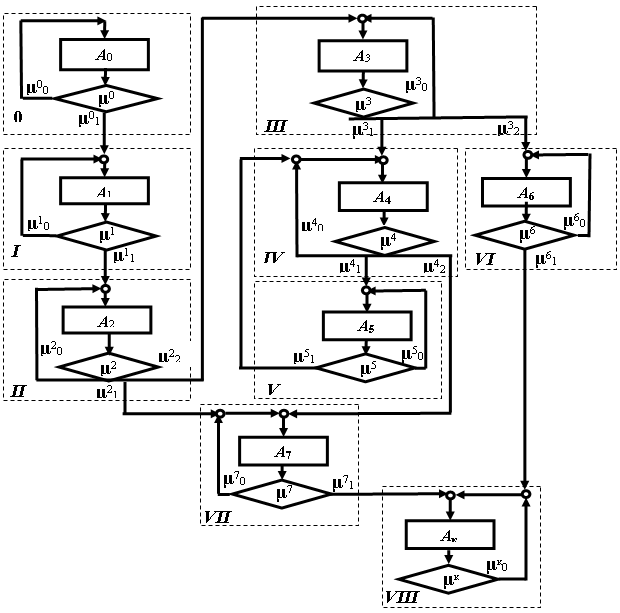
Рис. 2. «Доопределённая» граф-схема алгоритма
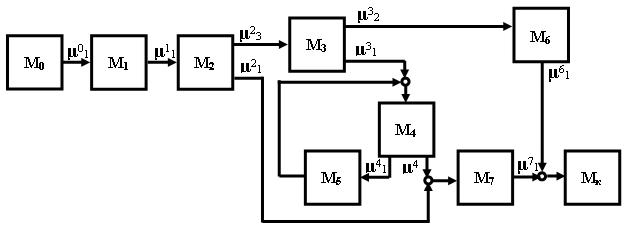
Рис. 3. Изображение алгоритма в модульном исполнении
Алгоритм можно задать в виде графа (рис. 4), вершины которого делятся на два непересекающихся множества, то есть граф будет дуальным.
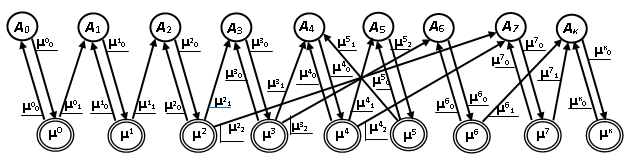
Рис. 4. Задание алгоритма в виде дуального графа
Использование матрично-предикатного способа представления графа [1–3] и представление алгоритма модулями (рис. 3), позволяет задать алгоритм в виде матрицы (рис. 5).
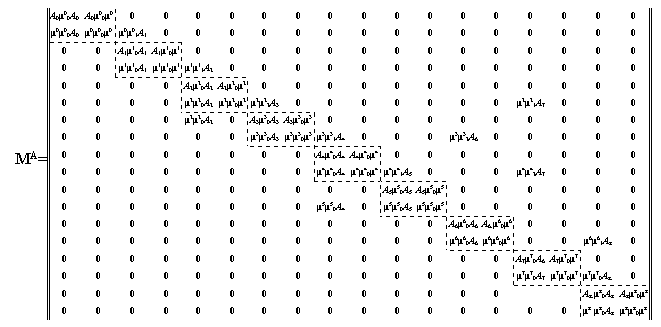
Рис. 5. Модульное представление алгоритма в матрично-предикатном виде
Такое представление алгоритма будем называть модульнымвматрично-предикатном виде.
Квадратная матрица алгоритма МA, заданная в матрично-предикатном виде, обладает неизменностью свойств описываемого объекта при одновременной замене строки и столбца с одинаковыми номерами на соответствующую пару с другим номером [4].
Проведём такую операцию с матрицей МA, разнеся функциональные и предикативные вершины алгоритма в противоположные стороны. В итоге получим описание того же алгоритма в виде МA* в несколько иной форме (рис. 6).
Такое представление алгоритма будем называть в матрично-предикатной форме.
Задание алгоритмов в матрично-предикатном виде позволяет проводить практически любые операции над ними. Недостатком является то, что при большом количестве компонентов вывод результатов на экран или бумагу получается очень громоздким. Это происходит из-за большой разреженности исходных матриц. Например, квадратная матрица (рис. 5) содержит 324 элемента, а значащих (ненулевых) всего 47.

Рис. 6. Функционально-предикативноепредставление алгоритма в матрично-предикатном виде
Такое соотношение значащих и нулевых элементов матрицы наводит на мысль использовать для представления алгоритма таблицу составляемую следующим образом.
Предположим, что рассматриваемый алгоритм (как оператор действия, так и оператор логики) представляют собой истинные значения двенадцатиместного предиката, описывающего рассматриваемый процесс.
Второе, третье и четвёртое места определяют процесс функционировния компонента. Места с 4-го по 12-е определяют свойства, положение, время функционировния и другие характеристики объекта в данной точке процесса.
Первая и последняя строки определяют связи истинных значений предиката между собой. Такую форму задания алгоритма будем называть таблично-предикатной.
Таблично-предикатная форма задания рассматриваемого алгоритма представлена ниже.
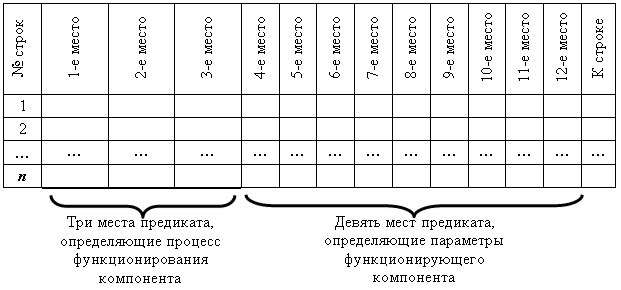
Рис. 7. Фрагмент задания алгоритма в таблично-предикатной форме
Рассмотрим матрично-предикатное представление алгоритма в модульном виде (рис. 5) и переход к таблично-предикатной форме. На рисунке (рис. 8) представлена таблично-предикатная форма задания рассмотренного алгоритма.
На рисунке (рис. 8) пунктиром выделены модули, 1–4 строчки — это первый модуль — I, 6–9 — это второй -II. После выполнения модуля I происходит выполнение перехода μ0 — μ01 — А1 (строка 5) и переход к выполнению модуля II.
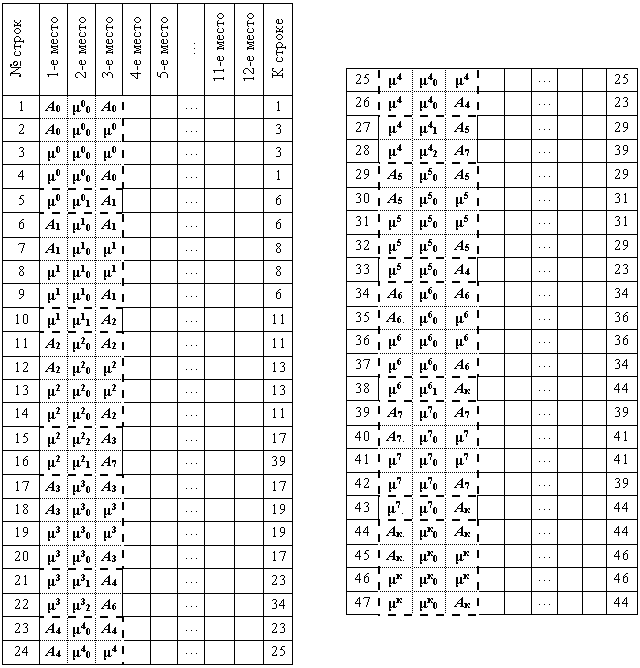
Рис. 8. Таблично-предикатная форма алгоритма заданного в модульном виде
Таким образом, кроме общепринятых способов алгоритм может быть задан в матрично-предикатном или таблично-предикатном виде.
Литература:
- Построение формального описания технологического процесса в матрично-предикатной форме / В. С. Поляков, С. В. Поляков, П. В. Федченков // Известия ВолгГТУ. Серия «Прогрессивные технологии в машиностроении». Вып. 9: межвуз. сб. науч. ст. / ВолгГТУ. — Волгоград, 2013. — № 7 (110). — C. 105–108.
- Поляков В. С., Поляков С. В. Запись алгоритма матрицей инцидентора // Инновации на основе информационных и коммуникационных технологий. Инфо 2014: матер. XI междунар.научн.-практ. Конф. (г. Сочи, 1–10 окт. 2014) /Национальный исследовательский ун-т «Высшая школа экономики» [и др.]. — М., 2014. — с. 149–152.
- Использование нагруженных матриц инцидентора (операторов) для моделирования сложных систем / В. С. Поляков, С. В. Поляков // Контроль. Диагностика. — 2013. — № 3. — C. 57–62.
- Поляков С. В., Сластинин С. Б., Поляков В. С. Исключение изоморфизма при операциях над графами, описывающими технологический процесс. // Контроль. Диагностика — 2006.– № 1







