Совершенствование расчета касательных напряжений в дорожных конструкциях. Часть 1. Модификация критерия Писаренко-Лебедева и его применение при расчете касательных напряжений



Предложен способ модификации критериев прочности твердых тел, состоящий в их преобразовании в условия пластичности, которые могут применяться для расчета материалов и грунтов дорожных конструкций по сопротивлению сдвигу. Суть предлагаемого способа состоит в подстановке в критерий прочности твердого тела зависимости, связывающей пределы прочности на сжатие и растяжение с параметрами предельной прямой Кулона-Мора. В результате такой модификации параметрами материала в усовершенствованном критерии являются сцепление и угол внутреннего трения. Используя модифицированный критерий Писаренко-Лебедева выполнен расчет касательных напряжений по глубине грунтового полупространства в сечении по оси симметрии нагрузки. Результаты этого расчета даны наглядно в виде эпюр.

Ключевые слова: критерий прочности, условие пластичности, главное напряжение, грунт, земляное полотно.

Сопротивление грунтов земляного полотна, а так же дискретных и монолитных материалов дорожной одежды, обуславливает величину, накапливаемой ими пластической деформации [1–5]. Учитывая то, что глубина неровности на поверхности покрытия дорожной одежды обусловлена пластическими деформациями материалов и грунтов дорожной конструкции [6] можно делать вывод о влиянии сопротивления сдвигу на равность покрытий автомобильных дорог. Так как специалисты дорожной отрасли единодушны во мнении, что допускаемая глубина продольных неровностей и колеи должна ограничиваться несколькими миллиметрами (в основном 4–30 мм) [7, 8], то обеспечение сопротивления сдвигу в материалах и грунтах дорожных конструкций является актуальной задачей.

Условия пластичности, применяемые для расчета грунтов и материалов по сопротивлению сдвигу можно условно подразделить три большие группы [1]:

 Аналитические, получаемые применением методов механики сплошной среды [1, 9, 10].

 Эмпирические, получаемые учетом экспериментальных данных при модификации аналитических условий [1, 11–16].

 Условия, учитывающие повреждения в структуре, монолитных материалов, полученные модификацией аналитических и эмпирических критериев сплошной среды [17, 18].

Аналитические условия пластичности, применяемые для расчета грунтов и материалов по критерию сопротивления сдвигу, приведены в табл. 1, составленной по материалам работ [1, 11–16].

Таблица 1

Аналитические условия пластичности дискретных материалов [1, 11–16]

Наименование условия	Математическое выражение
Кулона-Мора
где 1 и 3 — максимальное и минимальное главные напряжения, Па;  — угол внутреннего трения, град. или радиан; с — сцепление, Па.
Друкера-Прагера	; ; .
где J2 — второй инвариант девиатора напряжений, Па2; I1 — первый инвариант тензора напряжений, Па; а и k — параметры прочности, связанные с параметрами условия Кулона-Мора.
Ладе-Дункана	или ; При =0 kL–D=27
где kL–D — безразмерный параметр прочности грунта, связанный с углом внутреннего трения; I3 — третий инвариант тензора напряжений, Па3.
Матсуока-Накаи	или ; При =0 kM–N=9
где I2 — второй инвариант тензора напряжений, значение которого принимается по модулю, то есть положительным, Па2; kM–N — безразмерный параметр прочности грунта, связанный с углом внутреннего трения.

Эмпирические условия пластичности анализируются в работах [1, 11, 13, 14], в которых показано, что эти условия могут быть применены вместо традиционного критерия Кулона-Мора при расчете грунтов и материалов дорожных по критерию сопротивления сдвигу. Этот вывод следует из того, что касательные напряжения по эмпирическим критериям больше, чем по условию пластичности Кулона-Мора. Вследствие этого срок службы дорожной одежды запроектированной по эмпирическому критерию больше, чем по оригинальному условию пластичности Кулона-Мора, а значит, наилучшим образом соответствует результатам диагностики дорог, которые показывают, что накапливание покрытием предельных неровностей происходит гораздо быстрее, чем наступает предельное состояние по критерию Кулона-Мора.

Расширить базу эмпирических условий пластичности можно модификацией критериев порочности твердых сплошных тел. Для этой модификации можно воспользоваться формулами, связывающими пределы прочности на одноосное сжатие и растяжения с углом внутреннего трения и сцеплением. В этом случае после подстановки таких формул в оригинальный критерий прочности, он модифицируется путем замены пределов прочности на сцепление и угол внутреннего трения. Геометрический смысл такой модификации состоит в переходе от построения кругов Мора в плане сж — р (нормальное напряжение сжатия — нормальное напряжения растяжения) к построению кругов предельных напряжений в  —  плане (максимальное касательное напряжение — нормальное напряжение, которое перпендикулярно площадке с максимальным касательным напряжением).

Выполнив анализ условия Друкера — Прагера, записанного для сжатия и растяжения, можно прийти к выводу, что пределы прочности на одноосное сжатие и растяжение определяются по формулам [10–12]:

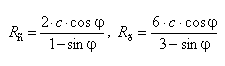(1)

В качестве модифицируемого критерия прочности примем оригинальный критерий Писаренко — Лебедева, который в оригинальном виде записывается уравнением [19, 20]:

,(2)

где и — интенсивность нормальных напряжений, Па.

При расчете дорожных конструкций считается, что в сечении по оси симметрии нагрузки 2=3. Учитывая это равенство и подставив в зависимость (2) формулы (1), после преобразований получим модифицированный критерий, предельное состояние которого определяется уравнением

(3)

В этом уравнении касательное напряжение записано в левой части, а правая часть уравнения (3) представляет собой прочностную характеристику, то есть сопротивление сдвигу. Анализируя левые части предлагаемого критерия (3) и оригинального условия Кулона-Мора можно убедиться, что касательные напряжения в уравнении (3) больше, чем по критерию Кулона-Мора. Это справедливо для всех значений углов внутреннего трения, за исключением случая =0. В том случае =0, уравнение (3) также как и оригинальный критерий Кулона — Мора вырождаются в третью теорию прочности, предельное состояние которой записывается уравнением:

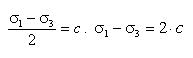(4)

Для расчета касательных напряжений по модифицированному условию пластичности (3) необходимо выполнить расчет максимального и минимального главных напряжений, которые непрерывно уменьшаются по глубине. В настоящее время для расчета напряжений в зернистых (дискретных) материалах и грунтах применяют формулы, полученные на основе методов механики сплошной или зернистой среды, а так же использованием инженерных методов расчета.

Анализ формул механики сплошной среды, выполненный в работах [1, 21] выявляет их недостатки, которые сдерживают их применение. Поэтому для расчета минимального главного напряжения автор воспользуется способом, найденным в работах [22, 23]. Суть этого метода состоит в том, что минимальное главное напряжение 3 определяют произведением трех функций: максимального главного напряжения 1, коэффициента бокового давления  и специальной функции глубина , называемой коэффициентом, характеризующим степень бокового расширения. Таким образом, расчет минимального главного напряжения выполняется по формуле

(5)

Формула для определения представляет собой функцию глубины, в которой параметром, изменяемым по глубине является коэффициент затухания (уменьшения) вертикального напряжения от равномерной нагрузки под осью ее симметрии формуле [23]:

(6)

где К — коэффициент затухания (уменьшения) вертикального напряжения от равномерной нагрузки под осью ее симметрии.

Коэффициент бокового давления может быть определен через коэффициент Пуассона [1] или угол внутреннего трения [24].

При расчете коэффициента бокового давления через коэффициент Пуассона зависимость (5) с учетом формулы (5) примет вид:

(7)

Для расчета коэффициента бокового давления через угол внутреннего трения можно воспользоваться материалами работ [1, 14, 24], в которых выполнено обобщение и анализ таких формул. Эти формулы приведены автором в табл. 2.

Таблица 2

Расчет коэффициента бокового давления через угол внутреннего трения

Автор формулы	Математическая запись
Г. И. Покровский
Ж. Биарез
Ж. Жаки
Жаки-Михайловский
Брукер-Иреланд
М. Д. Болтон

Примем зависимость (7) и модифицируем различные модели расчета главных напряжений. Представив максимальное главное напряжение произведением давления, передаваемого дорожной одеждой на земляное полотно и коэффициентом его затухания по глубине, являющимся функцией, получим формулу:

(8)

В таблице 3 приведены модифицированные модели А. Лява, М. И. Якунина и распределяющей способности, заимствованные автором из работ [25–27].

Таблица 3

Модифицированные модели для расчета главных напряжений от нагрузки, распределенной по гибко круглой площадке

Автор оригинального решения	Формулы модифицированной модели
1	2
А. Ляв
1	2
А. Ляв
где D — Диаметр круглой площадки, по поверхности которой распределена нагрузка, м;z — глубина, определяемая расстоянием от поверхности до рассматриваемой точки, м.
М. И. Якунин [18]
где а — коэффициент концентрации, принимаемый равным 1 (для нежестких дорожных одежд) или 2,5 (для упругих изотропных тел); с — показатель степени радикала, обычно принимаемый равным 2,5 или 3; Есл иЕосн — соответственно модуль упругости материала слоя и модуль упругости подстилающего основания, Па.
Модель распределяющей способности [19]
где  — угол рассеивания напряжения (иногда называют углом распределения давлений), град.

Выполнив подстановку формул таблицы 3 в предлагаемое модифицированное условие пластичности (3), выполним вычисление касательных напряжений, которые можно использовать при проектировании дорожных одежд. Результаты расчетов касательных напряжений приведены в виде эпюр на рисунках 1–3.

Рис. 1. Касательные напряжения, вычисленные по условию (3) при расчете главных напряжений по модифицированной модели А. Лява (µ=0,35)

Рис. 2. Напряжения, вычисленные по условию (3) при расчете главных напряжений по модифицированной модели М. И. Якунина (µ=0,35, Есл/Еосн=5)

Рис. 3. Касательные напряжения, вычисленные по условию (3) при расчете главных по модифицированной модели распределяющей способности (µ=0,35, α=40о)

Из анализируемых результатов расчета касательных напряжений, следует:

1. Независимо от принятой модифицированной модели расчета главных напряжений (см табл. 3) с увеличением угла внутреннего трения значение касательного напряжения уменьшается.
2. Величина угла внутреннего трения оказывает влияние на глубину расположения точки с максимальным касательным напряжением. Таким образом, от величины угла внутреннего трения зависит местоположение наиболее опасной точки и величина касательного напряжения в ней.
3. При расчете главных напряжений по модифицированным моделям М. И. Якунина и распределяющей способности на местоположение наиболее опасной точки обуславливается величиной параметров материалов, используемых в этих моделях. Такими параметрами являются отношение модулей Есл/Еосн и угол рассеивания напряжений α.

Литература:

1. Александров А. С. Совершенствование расчета дорожных конструкций по сопротивлению сдвигу. Ч. 1. Состояние вопроса: монография. — Омск: СибАДИ, 2015. — 292 с.

2. Семенова Т. В., Гордеева С. А., Герцог В. Н. Определение пластических деформаций материалов, используемых в дорожных конструкциях // Вестник Томского государственного архитектурно-строительного университета. — 2012. — № 4(37). — с. 247–254.

3. Александров А. С., Киселева Н. Ю. Пластическое деформирование гнейс- и диабаз материалов при воздействии повторяющихся нагрузок // Известия высших учебных заведений. Строительство. — 2012. — № 6. — с. 49–59.

4. Семенова Т. В., Герцог В. Н. Пластическое деформирование материалов с дискретной структурой в условиях трехосного сжатия при воздействии циклических нагрузок // Вестник Сибирской государственной автомобильно-дорожной академии. — 2013. — № 1(29). — с. 68–73.

5. Александров А. С. Пластическое деформирование гранодиоритового щебня и песчано-гравийной смеси при воздействии трехосной циклической нагрузки // Инженерно-строительный журнал. — 2013. — № 4(39) — с. 22–34.

6. Александров А. С. Применение теории наследственной ползучести к расчету деформаций при воздействии повторных нагрузок: монография. — Омск: СибАДИ, 2014. — 152 с.

7. Герцог В. Н., Долгих Г. В., Кузин В. Н. Расчет дорожных одежд по критериям ровности. Часть 1. Обоснование норм ровности асфальтобетонных покрытий // Инженерно-строительный журнал. — 2015. — № 5(57) — с. 45–57.

8. Александров А. С., Гордеева С. А., Шпилько Д. Н. О допускаемых и предельных значениях неровностей асфальтобетонных покрытий дорожных одежд жесткого типа // Автомобильная промышленность. — 2011. — № 2. — с. 31–35.

9. Болдырев Г. Г. Методы определения механических свойств грунтов. Состояние вопроса / Г. Г. Болдырев — Пенза: ПГУАС, 2008. — 696 с.

10. Александров А. С., Долгих Г. В., Калинин А. Л. Применение критерия Друкера-Прагера для модификации условий пластичности // Наука и техника в дорожной отрасли. — 2013. № 2. — с. 26–29.

11. Калинин А. Л. Применение модифицированных условий пластичности для расчета безопасных давлений на грунты земляного полотна. // Инженерно-строительный журнал — 2013. № 4(39). — с. 35–45.

12. Александров А. С., Долгих Г. В., Калинин А. Л. О допускаемых давлениях на грунты земляного полотна и слои дорожной одежды // Наука и техника в дорожной отрасли. — 2012. № 2. — с. 10–13.

13. Чусов В. В. Перспективы применения эмпирических условий пластичности грунтов и определение их параметров при трехосных испытаниях грунтов Вестник ВолГАСУ. — 2015. № 4(61). — с. 49–57.

14. Александров А. С. Совершенствование расчета дорожных конструкций по сопротивлению сдвигу. Ч. 2. Предложения: монография. — Омск: СибАДИ, 2015. — 262 с.

15. Александров А. С., Долгих Г. В. Калинин А. Л. Модификация критериев прочности сплошной среды для расчета грунтов земляного полотна по сопротивлению сдвигу // В сборнике: Архитектура. Строительство. Транспорт. Технологии. Инновации Материалы Международного конгресса ФГБОУ ВПО «СибАДИ». — Омск: СибАДИ, 2013. — с. 228–235.

16. Александров А. С., Калинин А. Л. Совершенствование расчета дорожных конструкций по сопротивлению сдвигу. Часть 1. Учет деформаций в условии пластичности Кулона-Мора // Инженерно-строительный журнал. — 2015. № 7(59). — с. 4–17.

17. Александрова Н. П., Александров А. С., Чусов В. В. Модификация критериев прочности и условий пластичности при расчетах дорожных одежд // Вестник Сибирской государственной автомобильно-дорожной академии. — 2015. № 1(41). — с. 47–54.

18. Александрова Н. П., Александров А. С., Чусов В. В. Учет поврежденности структуры асфальтобетона в критериях прочности и условиях пластичности // В сборнике:Политранспортные системыматериалы VIII Международной научно-технической конференции в рамках года науки Россия — ЕС. Новосибирск: СГУПС, 2015. — с. 219–225.

19. Лебедев А. А. О возможном совмещении условий пластичности и хрупкого разрушения // Прикладная механика. — 1968. — № 4 — с. 85–93.

20. Писаренко Г. С., Лебедев А. А. Деформирование и прочность материалов при сложном напряженном состоянии — Киев: Наукова Думка, 1976. — 416 с.

21. Долгих Г. В. Расчет грунтов земляного полотна по критерию безопасных давлений // Вестник Сибирской государственной автомобильно-дорожной академии. — 2013. — № 6 (34). — с. 43–49.

22. Александров А. С., Долгих Г. В. Расчет главных напряжений в слоях дорожной одежды из дискретных материалов // Транспортное строительство. — 2011. — № 7. — с. 17–22.

23. Александров А. С. Один из путей расчета минимальных главных напряжений в грунтах земляного полотна / А. С. Александров // В сборнике:Архитектура. Строительство. Транспорт. Технологии. ИнновацииМатериалы Международного конгресса ФГБОУ ВПО «СибАДИ». — Омск, СибАДИ, 2013. — с. 217–228.

24. Строкова Л. А. Учет переуплотнения грунтов в расчетах оседания земной поверхности при сооружении туннелей // Известия Томского политехнического университета. — 2010. — Т. 316. — № 1. — с. 147–151.

25. Александрова Н. П. Модифицированные модели для расчета главных напряжений в грунте земляного полотна // В сборнике:Архитектура. Строительство. Транспорт. Технологии. ИнновацииМатериалы Международного конгресса ФГБОУ ВПО «СибАДИ». Омск, 2013. — с. 236–246.

26. Александров А. С., Александрова Н. П., Долгих Г. В. Модифицированные модели для расчета главных напряжений в дорожных конструкциях из дискретных материалов // Строительные материалы. — 2012. — № 10. — с. 14–17.

27. Александрова Н. П. Совершенствование моделей расчета главных напряжений и девиатора в грунте земляного полотна / Н. П. Александрова, Т. В. Семенова, Г. В. Долгих // Вестник СИБАДИ. — 2014. — № 2(36). с. 49–54.