В статье приводится описание учебной компьютерной модели сложения двух взаимно перпендикулярных гармонических колебаний. Отмечается, что использование таких моделей в обучении физике способствует повышению наглядности и, как следствие, повышению эффективности обучения.
Ключевые слова: компьютерное моделирование, модель, механические колебания, сложение колебаний, учебные компьютерные модели, фигуры Лиссажу.
Сейчас под методикой обучения понимается, как правило, теоретическая и прикладная наука, предметом которой является научное обоснование целей, содержание обучения, а также разработка наиболее эффективных методов, приемов и форм обучения с учетом поставленных целей, содержания и конкретных условий обучения. Эффективность заново создаваемой системы обучения зависит от того, насколько последовательно эта система учитывает объективные закономерности, согласно которым происходит усвоение знаний в учебных условиях.
Одним из наиболее эффективных средств формирования новых знаний у обучающихся является повышение наглядности обучения, так как считается, что у человека преобладает наглядно-образное мышление, и информацию он воспринимает преимущественно образно. Принцип наглядности рассматривается как один из основных принципов в обучении. Наглядность увеличивает эффективность обучения, помогает обучающемуся усваивать знания с большим интересом. Значение наглядности заключается в том, что она мобилизует психическую активность обучающихся, вызывает у них интерес к занятиям, расширяет объем воспринимаемого учебного материала, часто снижает утомление, тренирует воображение, мобилизует волю и облегчает процесс обучения в целом.
Управление вниманием обучающихся предполагает следующие действия обучающего:
– преподаватель использует материал, интересный в содержательном плане;
– преподаватель обеспечивает каждому обучающемуся понимание и осознание смысла (мотивов и целей) предлагаемых учебных заданий и упражнений;
– преподаватель обеспечивает формирование знания способа выполнения заданий и упражнений;
– преподаватель создает обстановку, располагающую к сосредоточенному труду и непринужденному общению.
Обучающиеся лучше запоминают то, что вызывает их эмоциональный отклик и отвечает их интересам. Поэтому рекомендуется организовать обучение в таких ситуациях, которые связаны с их интересами и создают мотивы для общения и взаимодействия обучающихся между собой.
Таким образом, наглядность является незаменимым качеством обучения. Она является средством создания мотивационно-побудительного уровня общения, средством создания обстановки, приближенной к реальным условиям. Обучающий должен знать виды наглядности и характер визуального учебного материала, чтобы в определенной ситуации применить нужный наглядный образец этого материала.
Визуальный материал, используемый в обучении, можно разделить на следующие типы: статический и динамический.
Технические средства обучения служат для интенсификации работы обучающего [1, с. 142]. Они могут способствовать более полному и точному представлению информации об изучаемом явлении или объекте, а также улучшить наглядность обучения и облегчить усвоение учебного материала, который при обычных способах представления является сложным для понимания обучающихся [4].
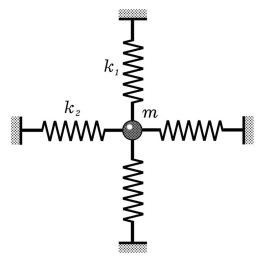
Рис. 1. Колебательная система
Компьютерная техника уже достаточно давно используется в процессе обучения, в том числе и как средство обучения. Она хорошо визуализирует учебный материал, но, в то же время, изменяет структуру и форму проведения занятий. Ее применение нельзя превращать в самоцель. Возможности современных компьютеров позволяют использовать их для моделирования процессов, которые раньше изучались только на умозрительном уровне. Использование учебно-методического комплекса, включающего в себя компьютерные модели, предназначенные для обучения (учебные компьютерные модели), может вывести преподавание физики на более высокий уровень в плане повышения наглядности обучения [3].
Рассмотрим, как повышается наглядность при обучении физике с помощью учебных компьютерных моделей на примере созданной нами модели сложения взаимно перпендикулярных колебаний. Моделируемая система представляет собой объект, изображенный на рис. 1. Это материальная точка массой m, которая имеет упругие связи с коэффициентами жесткости k1 и k2.
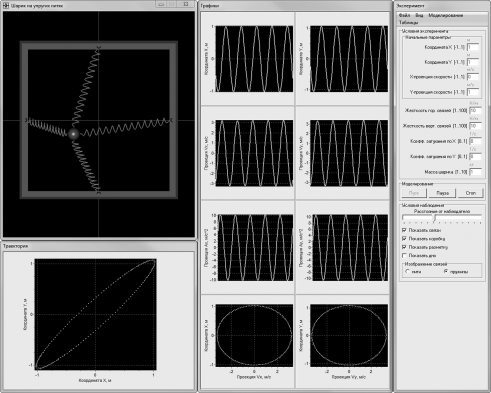
Рис. 2. Окна приложения, моделирующего сложение двух взаимно перпендикулярных гармонических механических колебаний
Приложение, моделирующее сложение колебаний, имеет четыре окна: окно для визуализации образной модели (непосредственно колебательной системы), окно для представления функциональных зависимостей характеристик образной модели от времени и фазовых диаграмм, окно для демонстрации траектории материальной точки, окно для элементов управления и вывода текущих значений характеристик образной модели (рис. 2) [2]. Программа предназначена для запуска в операционной системе типа WindowsXP и выше.
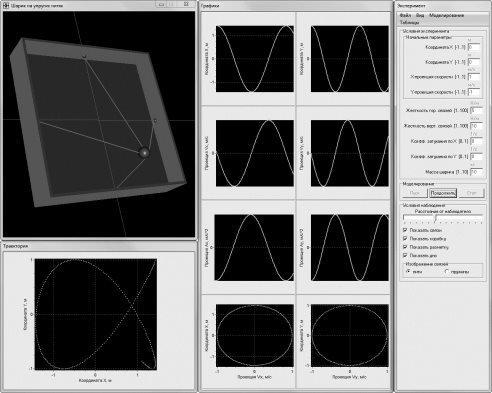
Рис. 3. Демонстрация сложения колебаний
Как известно траекториями материальной точки в данной ситуации будут кривые, которые называются фигурами Лиссажу. Обычно при изучении сложения колебаний сравнивают эти фигуры, полученные при определенных отношениях частот складываемых колебаний (1:1, 1:2, 1:3, 1:4, 2:1, 2:3 и т. п.) и сдвигах фаз колебаний (0, π/4, π/2, π, 3π/4). Программа позволяет получать картины колебаний при значительно большем количестве вариантов отношения частот и сдвигов фаз складываемых колебаний (рис. 3). На рис. 4 и 5 представлены картины колебаний при отношениях частот 1:2 и 1:3 соответственно и сдвигах фаз, равных π.
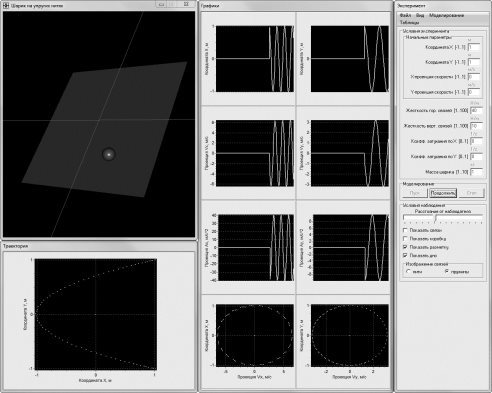
Рис. 4. Вариативность визуализации колебаний (отношение частот колебаний 1:2,
сдвиг фаз π)
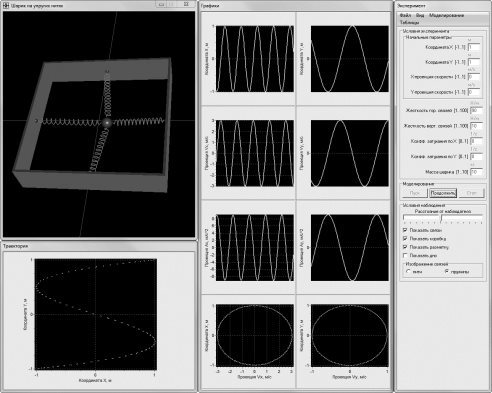
Рис. 5. Еще один вариант демонстрации сложения взаимно перпендикулярных колебаний (отношение частот 1:3, сдвиг фаз π)
В заключении отметим, что учебное компьютерное моделирование (учебный вычислительный эксперимент) нужно сочетать с учебным натурным экспериментом, и ни в коем случае не считать его полной заменой последнего.
Литература:
- Бушок Г. Ф. Методика преподавания физики в высшей школе / Г. Ф. Бушок, Е. Ф. Венгер. — Киев: «Освита Украины», 2009. — 415 с.
- Данилов О. Е. Дизайн компьютерных приложений для визуализации информации об учебных компьютерных моделях / О. Е. Данилов // Молодой ученый. — 2014. — № 13. — С. 26–36.
- Данилов О. Е. Использование компьютерных моделей маятников при изучении механических колебаний / О. Е. Данилов // Дистанционное и виртуальное обучение. — 2015. — № 7. — С. 40–47.
- Данилов О. Е. Экспериментальное изучение интерференции звука на плоском зеркале с помощью компьютерного сканирования / О. Е. Данилов // Инновации в образовании. — 2016. — № 1. — С. 106–114.







