Рассмотрены методы и задачи повышения качества, выделения контуров и сегментация изображений на основе нечетких множеств. Разработана структурная схема основных функциональных подсистем с учетом “мягких вычислений”.
Ключевые слова: система, нечеткие множества, нечеткая логика, изображения сегментации, контур, база знаний, база правил, компьютерное зрение.
Решение задачи определения границ (выделения контуров) объекта на изображении и его сегментация средствами аппарата нечеткой логики является актуальной.
Целью исследования является формализация задач выделения контуров объекта на изображении и его сегментация в терминах нечетких множеств.
Четко разграничивая поэлементные операции в задачах обработки изображений и правил, поэлементные операции выполняются по известным правилам матричной алгебры [1] попиксельно (например, говоря об операции деления одного изображения на другое, подразумеваем, что деление производится над соответствующими пикселями двух изображений). Методы, основанные на арифметических операциях над изображениями, являются поэлементными операциями, т.е. они применяются к паре соответствующих пикселей двух изображений [2, 3], и обозначаются следующим образом:
С(x, y)=U1 (x, y)+U2(x, y),
P(x, y)=U1 (x, y)-U2(x, y),
Y(x, y)=U1(x, y)*U2(x, y),
D(x, y)=U1 (x, y)/U2(x, y),
где хє{0, 1, 2, …М-1}, yє{0, 1, 2, …, N-1}, М и N – соответственно число строк и столбцов изображений, U1, U2 изображения C, P, Y, D – результат арифметических операций. Для решения данной задачи при очень малом уровне освещенности можно использовать метод уменьшения уровня на основе суммирования серии зашумленных изображений {Si(x, y)}, где S(x, y)=U(x, y)+SH(x, y), и значения шума SH(x, y), в каждой точке (x, y) являются некоррелированными и имеют нулевое среднее значение. Известно [2-4], что методы, основанные на пространственных операциях, осуществляются непосредственно над значениями пикселей обрабатываемого изображения и разделяются на три категории: 1) поэлементные операции; 2) в рамках определенного фрагмента; 3) глобальная обработка рассматриваемого изображения.
Исходя из яркости пикселей, модифицируются их значения, применяя поэлементные операции над цифровым изображением.
Поскольку результат поэлементной операции в любой точке обработанного изображения зависит только от значения входного изображения в этой же точке, она применяется как заключительный этап при решении более сложных задач.
В результате операции над окрестностью изменяетсясоответственный (х, у- координаты окрестности произвольной точки изображения - U) пиксель в выходном изображении φ. При этом значение рассматриваемого пикселя определяется с помощью операции над элементами исходного изображения с координатами из Wx, y (множества координат окрестности произвольной точки х, у). Определение усредненного значения яркости пикселей в прямоугольной окрестности определяется уравнением.
φ(x, y)= 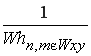 ∑U(n, m)
∑U(n, m)
где n, m - координаты строки и столбца для тех пикселей, координаты которых входят во множества W x, y , при этом предполагается что размер окна W*h, а центр в точке х, у.
Категории операций геометрических преобразований и совмещения изображений изменяют пространственные взаимосвязи между пикселями на изображении. Увеличение или уменьшение области пространственного преобразования осуществляется с определенными правилами цифровой обработки: 1) преобразование координат в пространстве; 2) интерполяция значении яркости в рассматриваемой окрестности; 3) комбинации указанных преобразований, в которых происходит присвоение значении яркости точкам изображения, подвергнутого пространственному преобразованию.
Известно, что многие изображения, рассматриваемые при решении прикладных задач, являются многоканальными. Эффективным инструментом при обработке таких изображений являются методы, основанные на векторных и матричных операциях [2]. В цветовом пространстве RGB каждый пиксель цветного изображения имеет 3 компонента
r=![]()
где r1, r2, r3 – соответственно яркости пикселя на красном, на зеленом и синем изображении. Делая соответствующее векторное представление пикселей, широкий круг линейных преобразований, применяемых к изображению, можно описать в единой форме
B=TA+ɤ
где, вектор А размерности MN*1 представляет исходное изображение, вектор ɤ размерности MN*1 представляет шумовую составляющую размерами M*N, вектор В размерности MN*1 представляет обработанное изображение, a T-матрица порядка MN*МN, которая задает линейное преобразование, применяемое к исходному изображению.
В некоторых случаях при решении задач фильтрации исходное изображение переводится в частотную область, а для возвращения обратно в пространственную область используется обратное преобразование [2]. Прямое преобразование – T(u, v) описывается в виде
![]()
где U(x, y) исходное изображение, g(x, y, u, v), называется ядром прямого преобразования и вычисляется для u=![]() 1, и v-
1, и v-![]() M и N – количества строк и столбцов в U. Имея T(u, v) можно восстановить U(x, y), применением к T(u, v) обратного преобразования
M и N – количества строк и столбцов в U. Имея T(u, v) можно восстановить U(x, y), применением к T(u, v) обратного преобразования
![]()
где g(x, y, u, v) называется ядром обратного преобразования.
Подходы, основанные на статистических методах, до сих пор рассматривались с использованием одной случайной величины (яркости), распределенной по одиночному изображению. В задачах, где необходимо время интерпретировать как третью переменную, требуется аппарат статических методов изображений, где рассматривается целое изображение (а не одну его точку) как случайное пространственное событие, что требует разработки аппарата случайных полей.
При работе с полутоновыми изображениями, понятия базовых операций над множествами основанных на теоретико–множественных логических операциях неприемлемы, потому что необходимо указать значение всех пикселей для результата операции над множествами. На самом деле, в случае полутонов, операции объединения и пересечения обычно определяются как соответственно максимум и минимум для пары соответственных пикселей, а дополнение определяется как попарные разности между константой и яркостью каждого пикселя.
Объединяя два полутоновых множества
A Ʋ B{![]() (a, b) |aєA, bєB},
(a, b) |aєA, bєB},
(где а, b – яркость изображение A и B соответственно в координатах (x, y) z –яркость в данной точке), можно получит массив, сформированный из максимальных значений яркости каждой пары соответственных пикселей.
Известно [5], что при морфологической обработке изображений, достаточно только три логические операцииAND, OR и NOT.
Нечеткие множества. Рассмотренные методы обработки, основанные на теоретико-множественных и логических операциях, сильно ограничивают возможности применение этих методов, поскольку они оперируют «четкими» множествами, т.е элемент принимает предельно пороговое значение: либо принадлежит, либо не принадлежит множеству. Это ограничивает использование классической теории множеств во многих практических приложениях. Поэтому вводится понятие функции принадлежности, которая должна быть гибкой и многозначной и обеспечила бы плавный переход от значения порога и её можно рассмотреть как основу нечеткой логики, а множества как «нечеткие множества». Использование нечетких множеств в обработке изображений является мощным инструментом для представления и обработки знаний, и они эффективно могут управлять неопределенностью и неоднозначностью.
Концепция нечетких множеств применяется к следующим задачам: повышения качества изображений, сегментации изображений и выделения контуров на изображение.
Известно, что усредняющие фильтры (фильтр для динамического уменьшения сужения диапазона значений яркости и повышения контраста использует подход, основанный на нечетких правилах) эффективно удаляют гауссов шум, а фильтры, основанные на порядковых статистиках, такие как медианный фильтр, эффективно используются для удаления импульсного шума. Для объединения этих двух фильтров применяется нечеткая логика.
Применение аппарата нечетких множеств позволяет включить в себя эвристические знания о его конкретном применении в виде правил и улучшения качества изображения, с учетом знаний экспертов в предметной области, чего нет в традиционных методах обработки изображений.
Задача выделения контуров непосредственно связана с определением зоны перепада яркости на границе между двумя областями. Поэтому требуется выбор способа измерения яркостных переходов на изображении для корректного определения “перепада”.
Мы знаем, что при движении вдоль профиля слева направо, первая производная обнаруживает: 1) разрыв в начале и конце наклонного участка; 2) постоянное положительное значение на протяжении склона; 3) равна нулю в областях постоянства яркости. Вторая производная положительна в точке перехода от темного участка к наклонному, отрицательна в точке перехода от наклонного участка к светлому, и равна нулю на линейном склоне и участках постоянной яркости. Практика обработки изображений показывает, что даже небольшой шум может оказывать значительное воздействие на первую и вторую производные, применяемые для обнаружения перепадов на изображениях, что затрудняет применение методов выделения границ или анализе производных.
Формулировка задачи выделения контуров в рамках теории нечетких множеств позволяет использовать нечеткие приращения, которые являются менее чувствительными к локальным изменениям структур изображения, таким как границы объектов. При этом функция принадлежности определяется таким образом, что она адаптируется к шумовым составляющим для выполнения нечеткого сглаживания и позволяет обеспечивать высокую степень различия между шумом и структурными объектами изображения.
Целью сегментации изображений является разбиение на однородные области. Однородность рассматривается в смысле сходства интенсивности света или типа текстуры внутри областей. Применение аппарата нечетких множеств в какой-то мере устраняет сложности связанные с определением понятия однородности области. В целях формализации задачи сегментации объекта в терминах теории нечетких множеств вводятся понятия “абсолютно однородная”, “однородная”, “не совсем однородная” и на основе этих понятий определяются функции принадлежности.
На основе выше изложенных целей и задач исследований, определена архитектура и структура [6] системы обработки изображений, основанной на концепции нечетких множеств. Изложены основные принципы разработки программного обеспечения и их функциональное назначение. Здесь применение нечеткой логики выступает в роли классификатора. Применение нечеткой логики в задачах обработки визуальной информации обосновывается также свойством обучаемости или адаптивности нечеткой логики к новым задачам, при этом сохраняется архитектура сети и алгоритм ее функционирования.
Дальнейшее исследование предполагает решение следующих задач:
- экспериментальные исследования разработанных алгоритмов при решении модельных задач;
- создание системы распознавания на базе разработанных алгоритмов нечеткой обработки изображений;
- создание базы данных по обрабатываемому изображению и проведение экспериментальных исследований в целях оценки качества выполнения обработки и точности распознавания.
Литература:
- Гантмахер Ф.Р. Теория матриц. – М: ФИЗМАТЛИТ. 2004. 550с.
- Гонзалес Р., Вуде Р. Цифровая обработка изображений. – М., Техносдера. 2005. –1072 с.
- Линдли К. Практическая обработка изображений на языке СИ: Пер. с анг.– М. Мир, 1996. – 512 с.
- Гризман И.С, Киригук В.С, Косих В.П. и др. Цифровая обработка изображений в информационных системах. Новосибирск: НГТУ, 2002. – 352 с.
- Мастецкий Л.М. Непрерывная морфология бинарных изображений: фигуры, скелеты, циркуляры. – М.:Физмат. лит, 2009. – 288 с.







