Методы расчета общей устойчивости цилиндрических оболочек, подкрепленных в продольном направлении цилиндрическими панелями



В статье излагаются прикладные методы расчета общей устойчивости цилиндрических оболочек, подкрепленных в продольном направлении цилиндрическими панелями, по конструктивно ортотропной схеме при центральном сжатии.

Ключевые слова: металлическиецилиндрические оболочки, усиление панелями, цилиндрические оболочки, жёсткость, тонкостенные оболочки, устойчивость, ребристые оболочки.

Введение. Одной из актуальных задач в области металлических конструкций является интенсивное развитие листовых металлических конструкций, которое должно идти по пути изыскания оптимальных конструктивных форм и размеров, совершенствования методов расчета и разработки прогрессивной технологии их изготовления и монтажа. Простейшей формой листовых конструкций являются круговые цилиндрические оболочки, которые при сравнительной простоте изготовления сочетают в себе функции несущих и ограждающих элементов. Оболочки сегодня широко используются во многих отраслях строительства. Наряду с этим, методы расчета таких конструкций требуют дальнейшего совершенствования.

В данной работе предложены инженерные методы расчета общей и местной устойчивости таких оболочек по конструктивно - ортотропной схеме при центральном сжатии.

Основные допущения, принятые для построения предлагаемых методов расчета. Как правило, несущая способность оболочки при осевом сжатии или изгибе определяется потерей местной устойчивости, поскольку ее критические напряжения значительно ниже расчетного сопротивления материала конструкции.

У подкрепленных вдоль образующих цилиндрическими панелями оболочек при действии центрального или внецентренного сжатия может произойти местная (локальная) или общая потеря устойчивости. Местная потеря устойчивости представляет собой выпучивание панели основной или подкрепляющей оболочки. При общей потере устойчивости происходит выпучивание основной оболочки совместно с подкрепляющими ее панелями, что приводит к разрушению всей конструкции.

Повышение пространственной жесткости оболочки в местах установки подкрепляющих панелей меняет характер волнообразования при потере устойчивости, что приводит к существенному увеличению критических напряжений общей потери устойчивости. Кроме того, из-за большой жесткости на кручение замкнутого контура, образуемого основной оболочкой и подкрепляющей ее панелью, наблюдается эффект защемления отдельных панелей основной оболочки по линиям их контакта с подкрепляющими панелями. Благодаря этому при небольшой ширине этих панелей значительно повышаются критические напряжения местной потери устойчивости оболочки. Подкрепление оболочки цилиндрическими панелями резко снижает влияние ее начальных несовершенств формы на величину критических напряжений.

При расчете общей устойчивости оболочки с дискретным подкреплением цилиндрическими панелями по конструктивно-ортотропной схеме жесткости подкрепляющих панелей на растяжение (или на сжатие) и изгиб "размазываются" по участку длины оболочки между этими панелями. Такая расчетная схема очень удобна для практического применения в инженерных расчетах. В то же время выбор более точных расчетных схем, учитывающих дискретный характер подкреплений и имеющих несомненный теоретический интерес, не всегда оправдан, так как после сложных расчетов таких идеализированных систем вводится весьма неопределенная, но очень существенная, поправка на влияние начальных несовершенств формы оболочки. Эта поправка [1, 2] для неподкрепленных оболочек зависит от качества их изготовления и колеблется в больших пределах (0,3 - 0,06) при отношении r/h соответственно от 50 до 2500. Для подкрепленных оболочек влияние начальных несовершенств формы еще недостаточно изучено и поэтому не отражено в нормативных документах. Только для ребристых оболочек в [3] получена статистическая оценка влияния несовершенств на их устойчивость.

В случае панельного подкрепления оболочек, кроме некоторых экспериментальных данных, отсутствуют какие-либо рекомендации по учету влияния начальных несовершенств на значения критических напряжений потери устойчивости. Таким образом, принятая конструктивно-ортотропная схема позволила создать прикладные методы расчета новой конструкции башен, выполненных в виде подкрепленных панелями оболочек, и является наиболее целесообразной.

При разработке прикладных методов расчета подкрепленных панелями оболочек, кроме принятой расчетной схемы, вводятся следующие допущения:

- гипотеза прямых нормалей относится к совокупному сечению оболочки и подкрепляющей ее панели;

- контакт оболочки и панелей осуществляется вдоль линий, т.е. не учитывается толщина панели в зоне контакта;

- панели основной оболочки считаются защемленными по линиям их контакта с подкрепляющими панелями;

- форма оболочки считается идеальной, а влияние различного рода несовершенств учитывается впоследствии введением поправочных коэффициентов, как это принято в расчетной практике;

- не учитывается смещение центров тяжести подкрепляющих панелей относительно срединной поверхности основной оболочки.

Расчет общей устойчивости оболочки, подкрепленной панелями, при центральном сжатии. Для определения критических напряжений подкрепленных панелями оболочек по конструктивно-ортотропной схеме были получены выражения приведенных жесткостных параметров из условия равенства деформации элемента реальной и эквивалентной оболочки.

Приведенные жесткостные параметры поперечных сечений оболочки определяются обычным методом [3]:

(1)

где: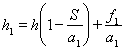– приведенная толщина поперечного сечения оболочки;

– цилиндрическая жесткость неподкрепленной оболочки;

h -толщина сечения основной оболочки;

ν -коэффициент Пуассона материала;

а1 -расстояние между осями симметрии подкрепляющих панелей;

S -длина дуги основной оболочки, заключенная между подкрепляющими панелями;

– погонный момент инерции подкрепляющей панели относительно центра тяжести совокупного сечения панели и оболочки;

f1 – суммарная площадь поперечного сечения подкрепляющей панели и замыкаемой ею части оболочки.

Приведенные жесткостные параметры продольных сечений определяются по формулам:

(2)

где: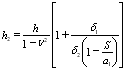– приведенная толщина продольного сечения оболочки.

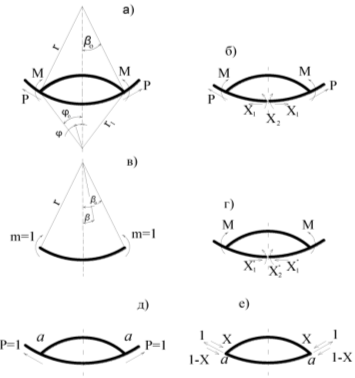
Рис.1. Расчетная схема, основная система к расчету замкнутой арочной рамы для определения приведенных жесткостных параметров подкрепленной цилиндрическими панелями оболочки

δ1 и φ1 – перемещение и угол поворота основной оболочки на участке подкрепляющей панели при действии единичной силы в направлении касательной к контуру срединной поверхности и единичного момента в окружном направлении;

δ2 и φ2 – перемещение и угол поворота для подкрепленной оболочки (замкнутого совокупного сечения) от той же силы и момента.

Для определения δ1, δ2 и φ1, φ2 раскрывается статическая неопределимость замкнутой арочной рамы, образованной основной оболочкой и подкрепляющей ее панелью (рис.1а). Неизвестные усилия X1 и Х2 (рис. 1б) определяются из канонических уравнений метода сил. Угол поворота (рис. 1в) в. случае круговых панелей определяется из следующей зависимости;

(3)

Перемещение находится из выражения, вытекающего из закона Гука, при растяжении (сжатии) для прямолинейных стержней

(4)

Угол поворота определяется с помощью формулы Моора. Для этого в основной системе (рис. 1б) полагаем М = 1, Р = 0 и из системы канонических уравнений метода сил находим неизвестные , которые прикладываем в месте разреза (рис. 1г):

(5)

где:-цилиндрическая жесткость подкрепляющей панели;

– толщина сечения подкрепляющей панели;

– момент, возникающий в основной оболочке от действия усилий

–момент, возникающий в подкрепляющей панели от действия этих же усилий;

;– усилия, возникающие соответственно в основной

оболочке и подкрепляющей панели от действия силы.

Перемещение δ1 определяется следующим образом (рис. 1д). Теоретически отделяем подкрепляющую панель от основной оболочки и прикладываем по концам неизвестное усилие X (рис. 1е). Перемещения в точке a концов оболочкии панелиравны между собой и равны δ2

(а)

Перемещение δ1 находится с помощью зависимости (4), а или и от сил X и Х-1 – по формуле Моора. Подставив выражения для δаили ив (а), определяем неизвестное усилие X. Зная усилие X, можно легко найти перемещение δ2.

Подкрепляющие цилиндрические панели совместно с основной оболочкой замыкают сравнительно большую площадь F (рис. 2). Благодаря этому они существенно повышают жесткость оболочки на кручение.

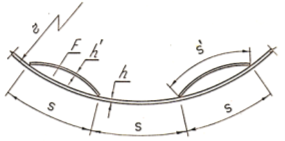
Рис.2. Фрагмент сечения оболочки, подкрепленной цилиндрическими панелями.

Приведенная жесткость на кручение определяется по формуле:

(6)

где: – погонная, отнесенная к длине a1, жесткость кручения замкнутого контура.

Величина находится следующим образом. По формуле Бредта при действии на ребро крутящего момента Мкр

Соответственно - относительный угол поворота по формуле Моора

,

где:– периметр совокупного сечения;

– некоторая средняя толщина оболочки;

S`– длина дуги подкрепляющей панели;

E, G– модули упругости и сдвига материала оболочки.

Отсюда

С другой стороны

Следовательно,

Из приведенного выражения видно, что жесткость оболочки на кручение увеличивается с возрастанием площади, которую охватывает подкрепляющая панель и основная оболочка.

Расчет общей устойчивости по полумоментной теории. Критические напряжения потери устойчивости определим используя допущения полумоментной теории [4], в частности:

- гипотезы о не растяжимости контура поперечного сечения оболочки

(7)

- гипотезы об отсутствии сдвигов в срединной поверхности оболочки

(8)

Задачу будем решать энергетическим методом по формуле С.П.Тимошенко. В полумоментной теории в энергию деформации включаются наиболее существенные, в данном случае, члены, связанные с изгибом оболочки в окружном направлении, депланацией поперечных сечений и кручением. Таким образом, уравнение для определения погонных критических усилий получает вид:

(9)

где: – относительная деформация, связанная с депланацией поперечных сечений;

– перемещения в направлении образующих, периметра и радиуса оболочки

при переходе к смежному равновесному состоянию;

– изменение при бифуркации окружной кривизны и кривизны кручения;

– погонный изгибающий момент в продольных сечениях оболочки и крутящий момент;

– отношение длины оболочки к ее радиусу;

– относительные (отнесенные к радиусу) координаты в направлении образующей и периметра оболочки.

С учетом (7) выражение кривизны получает вид:

(10)

кроме того:

(11)

После подстановки выражений (10), (11) в (9) и приравнивая его в соответствии с методом С.П.Тимошенко к нулю, получим уравнение

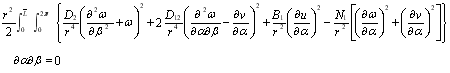(9)

Полагая, что торцы оболочки свободно оперты, будем считать, что форма потери устойчивости описывается выражением

(12)

Здесь: m=1,2,3, ...; n=2,3,....Числа натурального ряда m и n характеризуют соответственно число полуволн и волн, образующихся по длине оболочки и в направлении ее периметра.

Используя условия (7), (8), а также периодичность перемещений для замкнутой оболочки, получим:

(13)

После подстановки выражений в (9), интегрирования и простых преобразований получим выражение для

(14)

Минимизируя (14) по , найдем

(15)

Подставив выражение (15) в (14), получим формулу для определения минимального значения критического погонного усилия

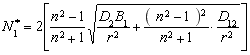(16)

Критические напряжения определяются по формуле:

(17)

Из формул (16), (17) видно, что критические напряжения увеличиваются с ростом изгибной жесткости оболочки в окружном направлении, жесткости на кручение и уменьшении ее радиуса, а наименьшее их значение получается при n = 2, если выполняется условие (15) при целочисленном значении .

Расчет общей устойчивости по моментной теории. Определим критические напряжения потери устойчивости оболочки по моментной теории. Задачу будем решать энергетическим методом Ритца.

Выражение энергии принимаем в виде:

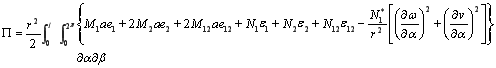(18)

где: – относителъная деформация, связанная с депланацией продольных сечений и деформация сдвига соответственно:

– погонные усилия продольных и поперечных сечений;

– погонное сдвигающее усилие;

– погонные изгибающие моменты в поперечных и продольных сечениях.

Примем форму потери устойчивости оболочки в виде:

(19)

Для деформаций и кривизны получим следующие зависимости:

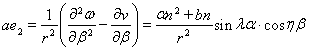(20)

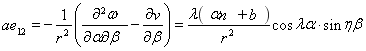
Погонные усилия и моменты выражаются следующим образом:

где приведенные коэффициенты Пуассона [4]:

(21)

После подстановки (20), (21) в (18) и интегрирования получим для энергии П алгебраическое выражение,

для которого запишем три условия экстремума

(22)

Из условия равенства нулю определителя однородной системы уравнений (22), при наличии нетривиальных значений коэффициентов a, b, c, получим выражение для критической нагрузки .Минимальное значениеможно найти после подстановки в это выражение приведенных жесткостных параметров, которые определяются по формулам (1), (2), (6), минимизируя его по m и n. Критические напряжения определяются по формуле (17).

Выводы:

- жесткостные параметры оболочки, подкрепленной открытыми цилиндрическими панелями, могут быть определены по предлагаемым формулам;

- предложен метод расчета устойчивости панели основной оболочки, подкрепленной круговыми панелями.

- разработана методика расчета общей устойчивости подкрепленной панелями цилиндрической оболочки по моментной и полумоментной теории при центральном сжатии, которые могут быть использованы в инженерных расчетах.

Литература:

1. СНиП И-23-81*. Стальные конструкции. Москва. 1998.

2. СНиП 2.03.05 – 97. Металл конструкции. Ташкент. 1997.

3. Липовский Д.Е. и др. Статистическая оценка влияния случайных возмущений на устойчивость ребристых оболочек по данным экспериментальных исследований. - В сб.: Расчет пространств, конструкций. Вып.17. М., Стройиздат, 1977, с.32-44.

4. Липовский Д.Е. Основы расчета оболочек строительных конструкций по моментной теории. Харьков, ХВВКУ, 1976, 104 с.