Теории турбулентности носят полуэмпирический характер, используя для своего построения экспериментальные данные. Эти теории для расчета пристенных турбулентных течений можно условно разделить на две группы. К первой группе относятся полуэмпирические теории турбулентности Прандтля, Кармана и другие, устанавливающие алгебраические связи между касательными напряжениями и градиентами осредненных скоростей [1]. Ко второй группе относятся численные методы интегрирования уравнений Рейнольса с помощью различных моделей турбулентности, которые, по существу, являются чисто эмпирическими. Но численные методы позволяют исследовать неизмеримо большее число турбулентных течений по сравнению с полуэмпирическими теориями, в основном за счет большего числа эмпирических констант, необходимых для реализации численных расчетов. Кроме того, для этой реализации необходимо задавать пристенные функции, если расчетная область располагается вблизи стенки.
Будем рассматривать дифференциальную феноменологическую модель течения вязкой несжимаемой жидкости — f˗модель [2], в определенном смысле альтернативную теории длины пути перемешивания. В ней содержится безразмерная скалярная величина ˗˗ некоторая весовая функция f, заключенная на промежутке от нуля до единицы и уравнение переноса этой величины. Эта функция представляет собой отношение турбулентной вязкости к суммарной, также включающей в себя молекулярную вязкость.
Согласно f˗модели, тензор Рейнольдсовых напряжений имеет вид:
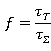
Причем
![]()
где ![]() ,
, ![]() и
и ![]() — суммарное, вязкостное и турбулентное касательные напряжения соответственно.
— суммарное, вязкостное и турбулентное касательные напряжения соответственно.
Как функция от перемещения и критерия Рейнольдса, ![]() обладает следующими свойствами:
обладает следующими свойствами: ![]() при
при ![]() и
и ![]() при
при ![]() .
.
В случае простого сдвигового течения:
![]() — вязкое напряжение для сдвиговых течений (Ньютон),
— вязкое напряжение для сдвиговых течений (Ньютон),
где ![]() — турбулентная вязкость.
— турбулентная вязкость.
Тогда ![]() откуда турбулентное касательное напряжение
откуда турбулентное касательное напряжение
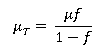
и в результате:
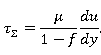 (1)
(1)
Для трехмерного случая (1) принимает вид:
![]() (2)
(2)
![]() — тензор суммарных напряжений,
— тензор суммарных напряжений, ![]() — тензор скоростей деформаций (осредненных, если поток турбулентен).
— тензор скоростей деформаций (осредненных, если поток турбулентен).
Выполним расчет течения жидкости в круглой цилиндрической трубе.
Согласно f˗модели:
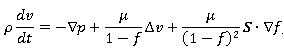 (3)
(3)
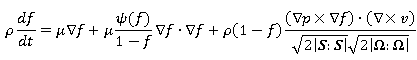 (4)
(4)
В уравнении движения (3) и уравнении (4) переноса безразмерной функции ![]() величины:
величины:
![]() ,
, ![]() — плотность;
— плотность; ![]() — давление;
— давление; ![]() — динамическая вязкость;
— динамическая вязкость; ![]() — вектор скорости;
— вектор скорости; ![]() — тензор скоростей деформаций;
— тензор скоростей деформаций; ![]() — тензор вращения;
— тензор вращения; ![]() — оператор материальной производной
— оператор материальной производной ![]() ;
;![]() — оператор Гамильтона (Набла).
— оператор Гамильтона (Набла).
Уравнение неразрывности:
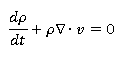 (5)
(5)
Система (3), (4), (5) описывает течение вязкой несжимаемой жидкости независимо от режима течения [3].
Краевые условия для этой системы уравнений — условия прилипания и вязкого ньютоновского трения на твердой границе Г с нормалью n, а также равенство нулю функции ![]() на этой стенке и условие на производную модуля скорости по этой функции:
на этой стенке и условие на производную модуля скорости по этой функции:
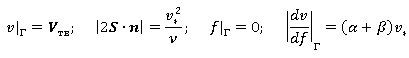 (6)
(6)
В этих выражениях ![]() — кинематическая вязкость;
— кинематическая вязкость; ![]() — скорость твердой границы;
— скорость твердой границы; ![]() — динамическая скорость, связанная с трением на стенке
— динамическая скорость, связанная с трением на стенке 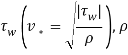 — плотность жидкости [4]. Схема течения представлена на рис.1.
— плотность жидкости [4]. Схема течения представлена на рис.1.
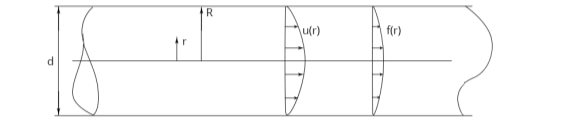
Рис. 1. Модель течения в круглой цилиндрической трубе
Будем решать задачу в цилиндрической системе координат ![]() . Для стабилизированного течения вектор скорости
. Для стабилизированного течения вектор скорости ![]() имеет лишь одну компоненту — осевую
имеет лишь одну компоненту — осевую ![]() , которая зависит только от одной координаты — радиальной. Обозначим
, которая зависит только от одной координаты — радиальной. Обозначим ![]() как
как ![]() . Величина
. Величина ![]() также зависит только от радиальной координаты,
также зависит только от радиальной координаты, ![]() . Уравнение движения (3), пренебрегая массовой силой, принимает вид:
. Уравнение движения (3), пренебрегая массовой силой, принимает вид:
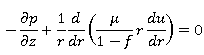
Для стабилизированного течения ![]() , и тогда можно перейти к обыкновенным производным:
, и тогда можно перейти к обыкновенным производным:
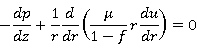 (7)
(7)
Уравнение переноса функции ![]() принимает вид:
принимает вид:
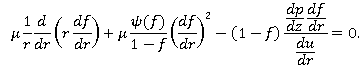 (8)
(8)
Уравнение неразрывности (5) тождественно удовлетворяется:
![]() .
.
Итак, в итоге получили систему (7), (8) из двух обыкновенных дифференциальных уравнений второго порядка. Их граничными условиями будут:
Введем следующие безразмерные переменные:
безразмерную радиальную координату, отсчитываемую от стенки трубы:
![]() .
.
На стенке, при ![]() величина
величина ![]() , а на оси, при
, а на оси, при ![]() ,
, ![]() Тем самым,
Тем самым, ![]() .
.
безразмерную скорость:
![]() , где
, где ![]() — динамическая скорость:
— динамическая скорость:
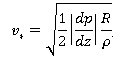
или
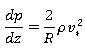
После введения этих переменных уравнения системы принимают вид:
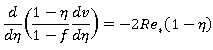 (9)
(9)
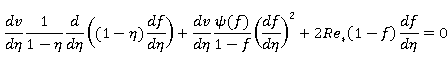 (10)
(10)
Здесь ![]() ,
, ![]() — кинематическая вязкость. Безразмерный комплекс
— кинематическая вязкость. Безразмерный комплекс ![]() связан с числом Рейнольдса
связан с числом Рейнольдса ![]() :
:
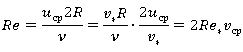
где ![]() — безразмерная средняя скорость по сечению трубы,
— безразмерная средняя скорость по сечению трубы,
![]()
Граничные условия для задачи (9), (10) после введения новых переменных принимают вид:
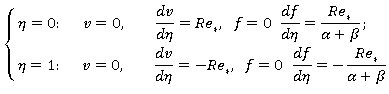 (11)
(11)
Ниже представлены результаты численных расчетов для различных чисел Рейнольдса в диапазоне от ![]() (ламинарный режим течения) до
(ламинарный режим течения) до ![]() (развитое турбулентное течение). На графиках (рис.2–5) изображены профили скоростей и меры турбулентности для соответствующих чисел Рейнольдса.
(развитое турбулентное течение). На графиках (рис.2–5) изображены профили скоростей и меры турбулентности для соответствующих чисел Рейнольдса.

Рис. 2. ![]()
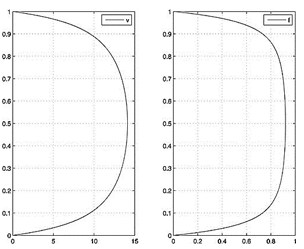
Рис. 3.
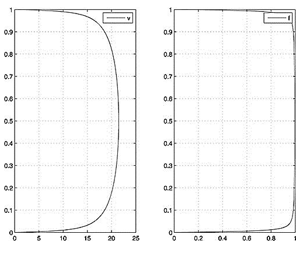
Рис. 4. ![]()
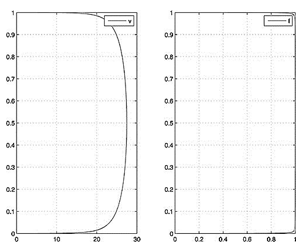
Рис. 5. ![]()
Уравнение (9) позволяет получить следующий первый интеграл
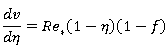 (12)
(12)
а (10) с учетом (12):
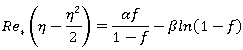 (13)
(13)
Подставляя в (12) продифференцированное по ![]() (13) и интегрируя полученное соотношение, получим соотношение для профиля скорости:
(13) и интегрируя полученное соотношение, получим соотношение для профиля скорости:
Для верификации численного решения системы, его надо сравнить с решением, полученным по формулам (13)˗(14) [5, 6]. Для этого сначала задается число Рейнольдса ![]() , вычисленное по динамической скорости, затем для каждого значения
, вычисленное по динамической скорости, затем для каждого значения ![]() по формуле (13) находятся профили скоростей
по формуле (13) находятся профили скоростей ![]() , а также определяются соответствующие значения функции
, а также определяются соответствующие значения функции ![]() . Далее вычисляется
. Далее вычисляется ![]() и
и ![]() . Кроме того, находится коэффициент сопротивления:
. Кроме того, находится коэффициент сопротивления:
![]()
Результаты расчета коэффициента сопротивления для различных чисел Рейнольдса на промежутке от ![]() до
до ![]() представлены на графике (рис.6):
представлены на графике (рис.6):
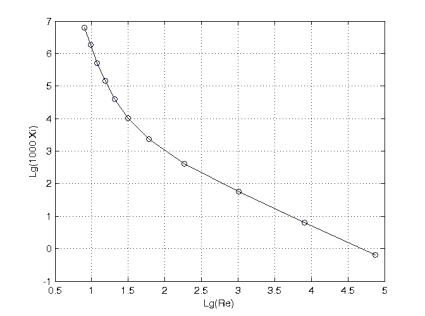
Рис. 6. Коэффициент сопротивления для различных Re
Сравнение численного результата с результатом, полученным т. н. полуаналитическим методом по формулам (13)˗(14) и рассматриваемым в качестве достоверного показывает, что отклонения не превышают допустимой погрешности.
На основе f˗модели были численно получены значения профилей скоростей и величин мер турбулентности при разных значениях числа Рейнольдса. Верификация полученных значений позволяет говорить о широкой применимости f˗модели для решения задач данного типа.
Литература:
- Шлихтинг Г. Теория пограничного слоя. М.: Наука. 1974. — 712 с.
- Павловский В. А. Об одной чисто феноменологической теории, альтернативной гипотезе пути перемешивания // Физическая механика. — вып. 7. Модели механики сплошной среды. СПб. СПбГУ. 1998. с. 21˗35.
- Макунин А. В. Применение f˗модели для расчета пристенных течений несжимаемой вязкой жидкости // Процессы управления и устойчивость. Том 2(18). № 1. СПб.: Издательский дом Федоровой Г. В., 2015. с. 213˗216.
- Чистов А. Л. Единая ламинарно˗турбулентная дифференциальная модель для течения вязкой несжимаемой жидкости. Вестник СПбГУ. Сер.10. 2008, вып. 4, с. 103˗106.
- Павловский В. А. Расчет кругового течения Пуазейля для произвольных чисел Рейнольдса // Проблемы экономии топливно˗энергетических ресурсов на предприятиях и ТЭС: Межвуз. сб. науч. тр./ СПб. ГТУ РП. СПб. 1999. с. 121˗126.
- Павловский В. А., Чистов А. Л. Расчет плоского напорного течения Куэтта при произвольных числах Рейнольдса // Проблемы экономии топливно˗энергетических ресурсов на предприятиях и ТЭС: Межвуз. сб. науч. трудов. / ГОУВПО СПбГТУ РП. 2009. с. 5˗12.







